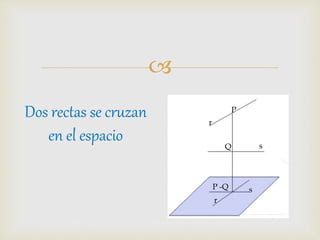
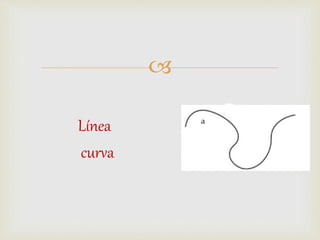
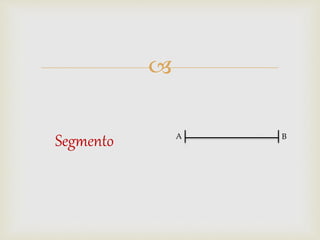
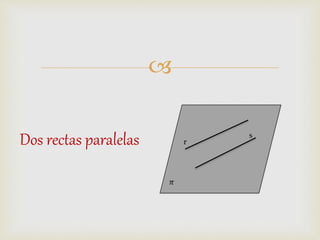
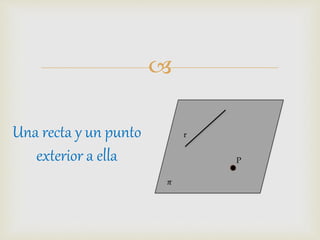
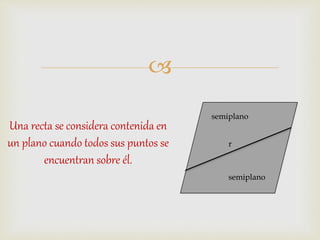
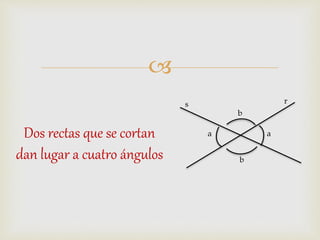
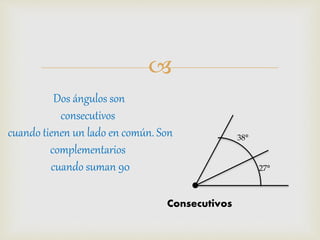
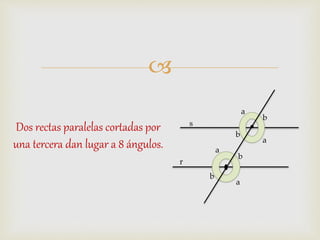
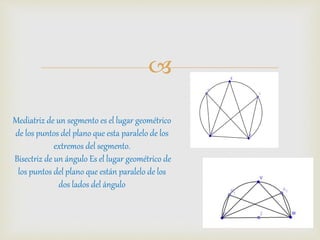
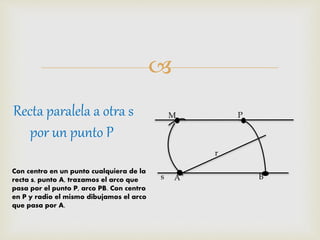
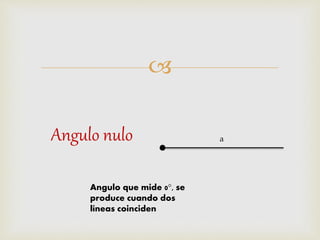
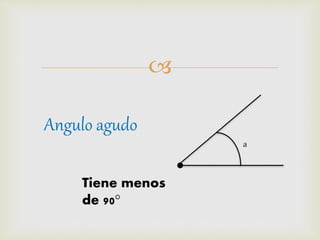
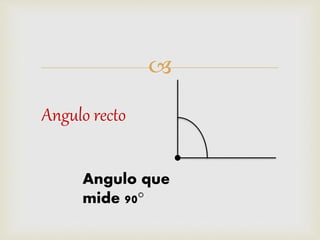
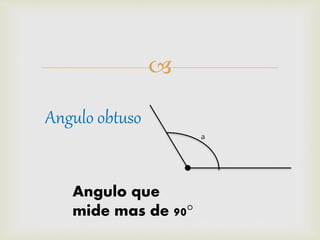
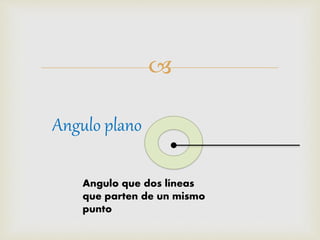
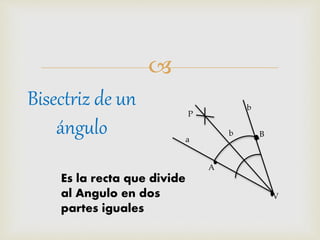
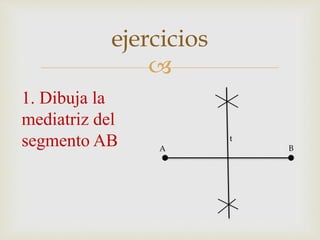
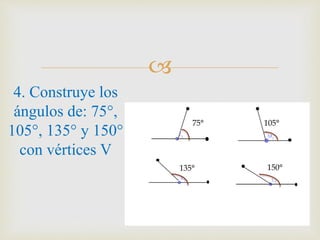
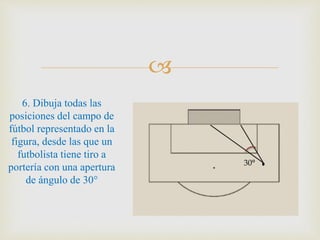
1) El documento presenta diferentes conceptos geométricos como líneas, ángulos, figuras planas y sus relaciones. 2) Se explican métodos para construir rectas perpendiculares, paralelas, bisectrices de ángulos y segmentos, así como formas de medir ángulos comunes. 3) También se definen conceptos como circunferencia, radio, diámetro, cuerda, secante y tangente.

1. Por: Mariana Muñoz
Brayan florez
11-02 JM

2. 
Línea
recta
r

3. 
Posiciones relativas
entre rectas
r
s
B

4. 
Dos rectas
paralelas
a
b∞

5. 
Dos rectas se cruzan
en el espacio
P
Q
r
s
s
r
P -Q

6. 
Línea
curva
a

7. 
Semirrecta r
P
A

8. 
Segmento A B

9. 
Plano
r
d
𝜋

10. 
Tres puntos no
alineados
A
B
C
𝜋

11. 
Dos rectas que se
cortan
P
r s
𝜋

12. 
Dos rectas paralelas r
s
𝜋

13. 
Una recta y un punto
exterior a ella
r
P
𝜋

14. 
Una recta se considera contenida en
un plano cuando todos sus puntos se
encuentran sobre él.
r
semiplano
semiplano

15. 
Mediatriz de un
segmento
Es la recta perpendicular al
segmento en su punto
medio.
2
1
M
m
12
N
A B

16. 
Perpendicular a una
recta t por un punto
exterior M
En M y con radio arbitrario r
trazamos un arco que corta a la
recta en los puntos A y B.
B
Q
12
t
m
A
12
P
M

17. 
Perpendicular a una recta
por un punto P
Concentro en P trazamos un arco de
radio arbitrario que al cortar a la
recta, determina los puntos A y B.
12
M
m
r
P
N
12

18. 
Perpendicular a una
semirrecta P-r en su
extremo
P
Concentro en P trazamos un arco
de radio PA arbitrario. Con centro
en A trazamos otro arco del mismo
radio que corta al arco anterior en
el punto B.
AP r
M
m
B
C

19. 
Recta paralela a otra s
por un punto P
Con centro en un punto cualquiera de la
recta s, punto A, trazamos el arco que
pasa por el punto P, arco PB. Con centro
en P y radio el mismo dibujamos el arco
que pasa por A.
P
BA
M
r
s

20. 
Angulo nulo
Angulo que mide 0°, se
produce cuando dos
líneas coinciden
a

21. 
Angulo agudo
a
Tiene menos
de 90°

22. 
Angulo recto
Angulo que
mide 90°

23. 
Angulo obtuso
Angulo que
mide mas de 90°
a

24. 
Angulo llano
Angulo que
mide 180°
a

25. 
Angulo plano
Angulo que dos líneas
que parten de un mismo
punto

26. 
Dos rectas que se cortan
dan lugar a cuatro ángulos
b
b
aa
s r

27. 
Dos ángulos son
consecutivos
cuando tienen un lado en común. Son
complementarios
cuando suman 90
38°
27°
Consecutivos

28. 
Dos rectas paralelas cortadas por
una tercera dan lugar a 8 ángulos.
s
r
a
a
b
b
a
a
b
b

29. 
Bisectriz de un
ángulo
V
A
Bb
P
a
b
Es la recta que divide
al Angulo en dos
partes iguales

30. 
Angulo de 60°
Una semirrecta Vr y cualquier radio
dibujamos un arco que corta a la
semirrecta en A, Se traza otro arco
que corta al anterior en B.
V
rA
B

31. 
Angulo de 90°
Basta con trazar por el
extremo de una semirrecta la
perpendicular ala misma
90°
45°

32. 
Angulo de 30°
Se divide un
Angulo de 60
30°

33. 
Angulo de 135°
Sumando uno de 90°
con otro de 45°

34. 
Circunferencia es el lugar geométrico de los
puntos del plano que equidistan del centro a
la superficie comprendida dentro de la
circunferencia.

35. 
Mediatriz de un segmento es el lugar geométrico
de los puntos del plano que esta paralelo de los
extremos del segmento.
Bisectriz de un ángulo Es el lugar geométrico de
los puntos del plano que están paralelo de los
dos lados del ángulo

36. 
Trazamos para ello la mediatriz del
segmento MN. Con vértice en M
dibujamos el ángulo complementario de
60°, o sea de 30°. El lado de este ángulo
corta a la mediatriz del segmento en el
punto O.

37. 
Radio es todo segmento r que tiene un extremo en el centro de la
circunferencia y el otro sobre ella.
Diámetro: Es el segmento d que une dos puntos de la
circunferencia alineados con su centro.
Cuerda: Es el segmento c que une dos puntos de la curva sin pasar
por su centro. Secante: Es la recta s que corta a la circunferencia en
dos de sus puntos. Tangente: Es la recta t que tiene sólo un punto
común con la circunferencia.

38. 
1. Dibuja la circunferencia que pasa por tres puntos conocidos
A,B y C
B
A
C

39. 
2. Hallar sobre el mapa de costa de la figura la posición P de un barco de altamar desde el que un
tripulante observa tres faros conocidos de la costa. A, B y C, bajo ángulos APB= 30° y BPC=45°

40. 
3. Un pirata enterró su tesoro en un lugar de una pequeña isla procediendo del siguiente
modo. Partiendo de una palmera, punto P, empezó a caminar en línea recta hasta llegar
después de recorrer 20m, a un punto T desde el que divisaba dos grandes rocas A y B
con una apertura de Angulo de 60°. Comprobó también que este lugar estaba mas cerca
de A que de B. Conociendo sobre el mapa las posiciones de las rocas A y B y de la
palmera B, dibuja sobre el mismo la posición T del tesoro
A B
T
P
O
30°

41. 
1. Dibuja la
mediatriz del
segmento AB
ejercicios
A B
t

42. 
2. Traza la recta
tangente en T a la
circunferencia
dada.
T

43. 
3. Divide el ángulo
de la figura en
cuatro partes
iguales.
a
b
c
d
e

44. 
4. Construye los
ángulos de: 75°,
105°, 135° y 150°
con vértices V
75° 105°
135° 150°

45. 
5. Dibuja, partiendo del
punto A, y utilizando la
escuadra, el cartabón y
la regla graduada, el
polígono de la figura.

46. 
6. Dibuja todas las
posiciones del campo de
fútbol representado en la
figura, desde las que un
futbolista tiene tiro a
portería con una apertura
de ángulo de 30°
30°