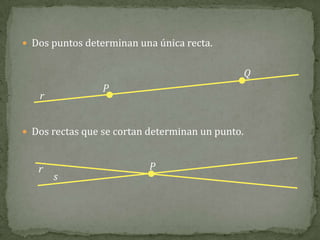
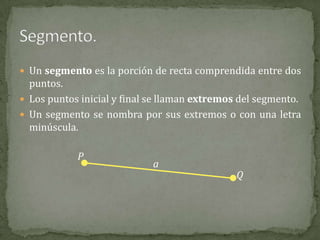
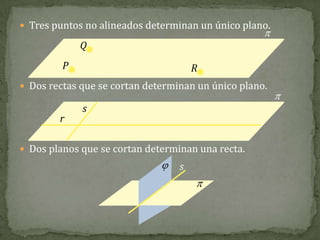
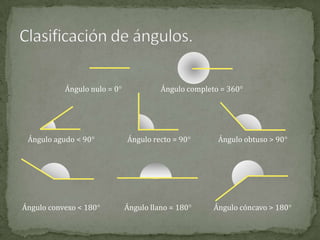
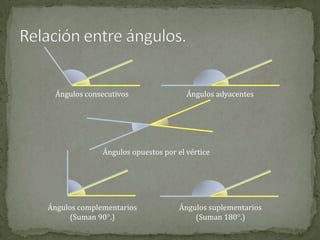
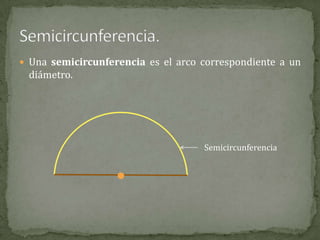
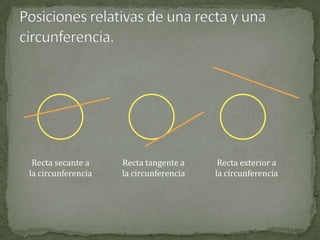
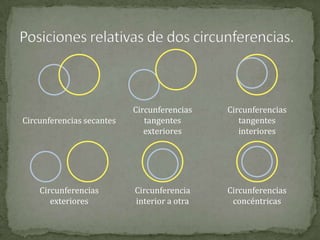
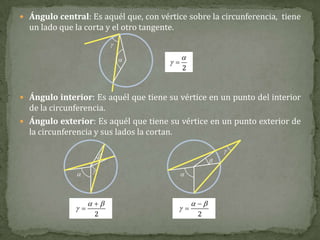
El documento define conceptos básicos de la geometría como puntos, rectas, planos, ángulos y circunferencias. Explica que un punto indica una posición, una recta está formada por puntos infinitos, y un plano por rectas infinitas. También describe elementos como segmentos, semirrectas, bisectrices y mediatrices, y sus relaciones.