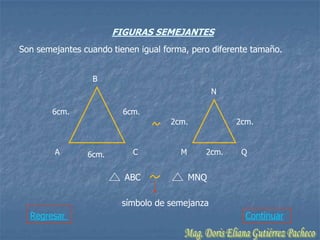
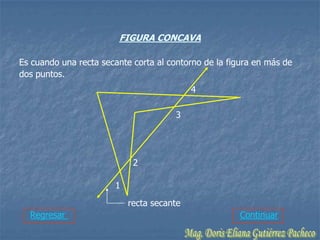
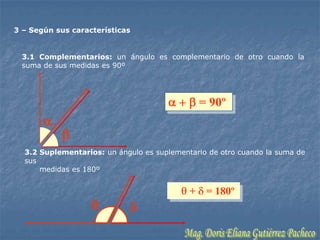
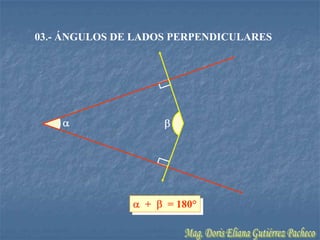
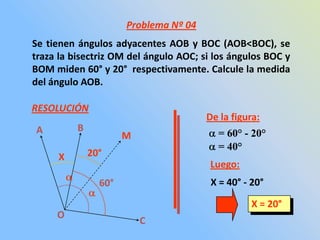
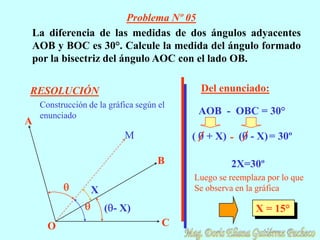
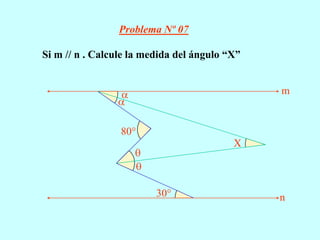
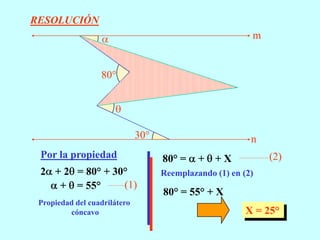
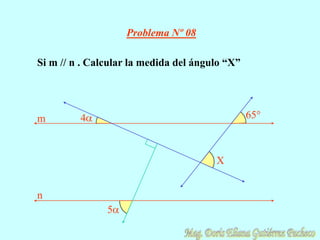
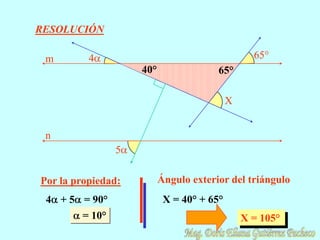
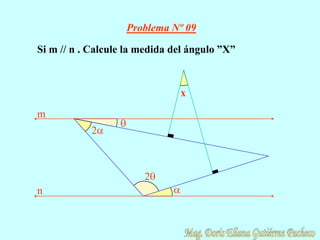
El documento resume conceptos geométricos fundamentales como puntos, rectas, planos, figuras geométricas y ángulos. Explica conceptos como figuras congruentes, semejantes y equivalentes, así como figuras convexas y cóncavas. También define líneas, partes de líneas rectas y clasificaciones y propiedades de ángulos. Finalmente, incluye ejemplos de problemas geométricos y su resolución.

2. 1. CONCEPTOS GEOMETRICOS
FUNDAMENTALES
2. FIGURAS GEOMETRICAS
3. LINEAS
4. ANGULOS
5. TRIANGULOS
6. AREAS DE REGIONES PLANAS
7. CUADRILÁTEROS
8. CIRCUNFERENCIA
9.- EJERCICIOS DE APLICACIÓN

3. PUNTO ESPACIO
RECTA PLANO
Regresar Continuar

4. EL PUNTO
La idea intuitiva de un punto geométrico nos da la marca que deja en el
papel la punta bien afilada de un lápiz, o un grano de arena muy
pequeño.
El punto no tiene dimensión.
Se le representa por el punto ortográfico (.) y colocando una letra
mayúscula al costado. Así:
A. P. K.
punto A punto P punto K
Regresar Continuar

5. LA RECTA
La recta es una sucesión infinita de puntos alineados, por eso es que
posee una longitud infinita.
.............
A las rectas se les representa:
L m .
A
. B
recta L recta m recta AB
Regresar Continuar

6. EL PLANO
La superficie del piso, una hoja de papel, la superficie de una pizarra, nos dan
la idea intuitiva del plano geométrico.
Un plano geométrico es una superficie ilimitada que no tiene espesor.
Se le representa:
P Q
Plano Q
Plano P
Regresar Continuar

7. ESPACIO
La idea intuitiva de espacio , viene a ser una extensión indefinida de
tres dimensiones es decir un lugar tan grande donde caben todos los
objetos reales o imaginarios.
Regresar Continuar

8. Una figura geométrica es un conjunto de puntos que tiene forma,
tamaño y posición. Se clasifica:
Figuras congruentes Figuras semejantes
Figuras equivalentes Figura convexa
Regresar Figura cóncava Continuar

9. FIGURAS CONGRUENTES
Son aquellas que tienen igual forma y tamaño.
B C Q R
4cm. 4cm.
=
A D P S
4cm. 4cm.
ABCD = PQRS
símbolo de congruencia
Regresar Continuar

10. FIGURAS SEMEJANTES
Son semejantes cuando tienen igual forma, pero diferente tamaño.
B
N
6cm. 6cm.
2cm. 2cm.
A 6cm. C M 2cm. Q
ABC MNQ
símbolo de semejanza
Regresar Continuar

11. FIGURAS EQUIVALENTES
Son equivalentes cuando tienen diferente forma, pero igual tamaño.
A . 12cm.
. B
<
3cm.
.N
5cm.
>
M
.
Longitud AB=longitud MNQR . .R
Q 4cm.
Área(1) = área(2)
< < : Símbolo de
> >
equivalencia
(1) (2)
Regresar Continuar

12. FIGURA CONVEXA
Es cuando una recta secante corta al contorno de la figura como
máximo en dos puntos.
.2 Recta secante
.1
Regresar Continuar

13. FIGURA CONCAVA
Es cuando una recta secante corta al contorno de la figura en más de
dos puntos.
4
3
2
1
recta secante
Regresar Continuar

14. a. Líneas rectas b. Líneas curvas
. . L .
A B .
c. Línea mixta
. . d. Línea quebrada o poligonal
. .
.
e. Partes de la línea recta
Regresar Continuar

15. Partes de la Línea recta
 Semirrecta:  Rayo:
A A
C B C B
origen origen
semirrecta AB semirrecta AC rayo AB rayo AC
• Segmento: Porción de línea recta comprendida entre dos puntos
. .
A B
5cm. AB : Se lee segmento AB
AB = BA
AB= 5cm o m AB = 5cm.
4cm. M 4cm.
AM = MB AM = MB = AB
A B 2
Regresar Continuar

16. EJEMPLOS
1.-Sobre una recta se toma 3 puntos consecutivos A;B;C. De tal manera que
BC =3AB.hallar la longitud de AB si AC =36cm
AB + BC = AC A B C
x+3x=36 x 3x
4x= 36 AB= 9cm
x=9cm
2.-sobre una recta se toma los puntos A;B;C y D en forma consecutiva de modo
que AC=18m; BD=16m y AD= 30m.determina la longitud de BC
AB + BD = AD A B C D
AB+16 = 30
AB= 14 18cm
AB +BC =18 16cm
14 +BC =18 30cm
BC=4 cm

17. ANGULOS
1. ANGULOS ESPECIALES
2. TEOREMAS DE LOS ANGULOS
3. PROPIEDADES DE LOS ANGULOS
4. POSICIONES RELATIVAS DE DOS RECTAS EN EL PLANO
5. ANGULOS FORMADOS POR DOS RECTAS PARALELAS AL
SER CORTADAS POR UNA RECTA SECANTE
6. PROPIEDADES DE LOS ANGULOS ENTRE PARALELAS
Continuar Regresar

18. ANGULO.-Es la abertura formado por dos rayos
divergentes que tienen un extremo común que se denomina
vértice.
ELEMENTOS DE UN ANGULO: A
O
B

19. CLASIFICACIÓN DE ÁNGULOS
1 – Según su medida
A A
A
B
O B O B O
Agudo: AÔB 90º Recto: AÔB = 90º Obtuso: AÔB 90º
A
A B O
O B
LLano: AÔB = 180º
Completo: AÔB = 360º

20. 2 – Según su posición
2.1 Consecutivos: son ángulos que tienen el mismo vértice y un lado común
A B
AÔB y BÔC son ángulos consecutivos
O C
2.2 Adyacentes: son dos ángulos consecutivos cuyos lados no comunes son
líneas opuestas
B
A AÔB y BÔC son ángulos adyacentes
C
O
2.3 Opuestos por el vértice: Son aquellos cuyos lados de uno son las
prolongaciones en sentido contrario de los lados del otro
A B AÔB y DÔC son ángulos opuestos por el vértice
D O AÔD y BÔC son ángulos opuestos por el vértice
C

21. 3 – Según sus características
3.1 Complementarios: un ángulo es complementario de otro cuando la
suma de sus medidas es 90º
= 90º
3.2 Suplementarios: un ángulo es suplementario de otro cuando la suma de
sus
medidas es 180º
+ = 180º

22. 4 – Ángulos especiales
Ángulos consecutivos son dos o
b a
más ángulos que tienen un (7)
mismo vértice y un lado común
dos a dos, tales como a, b y c (7) c
La Suma de las medidas de dos
o más ángulos consecutivos
b
formados en un recta es 180º. (8)
a c
ASI a+b+c=180º (8)
La Suma de las medidas de dos o
más ángulos consecutivos e
formados en un plano es 360º f d (9)
ASI d+e+f+g+h=360º
g h
Ángulos opuestos por el vértice
son dos ángulos cuyos lados
forman dos pares de rayos
opuestos tales como x y z (10)
x z (10)
Continuar Regresar

23. Rectas oblicuas:
Dos rectas en el plano son oblicuas cuando al cortarse forman cuatro ángulos diferentes de un
ángulo recto.
L
1
La notación: L L1
L
Rectas perpendiculares:
Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos rectos.
L La notación: L L
1
L
1
Continuar Regresar

24. Rectas paralelas:
Dos rectas en un plano son paralelas cuando por más que se
prolonguen no llegan a cortarse.
L
La notación: L // L
L1 1
Continuar Regresar

25. Ángulos externos: 1, 2, 7, 8
S
1
Ángulos internos: 3, 4, 5, 6
2 L
3 4
Ángulos alternos externos: 1 y 8, 2 y 7
5 6 L
1 Ángulos alternos internos: 3 y 6, 4 y
7
5
8
Ángulos correspondientes: 1 y 5, 2 y 6, 3 y 7, 4 y 8
Ángulos conjugadas externas: 1 y 7, 2 y 8
Ángulos conjugadas internas: 3 y 5, 4 y 6
Continuar Regresar

26. TEOREMAS: 1.- Los ángulos alternos externos son
S congruentes: m<1 = m<8
m<2 = m<7
2.- Los ángulos alternos internos son
1 2 L
congruentes: m<3 = m<6
3 4
m<4 = m<5
5 6 L 3.- Los ángulos correspondientes son
1
7
congruentes: m<1 = m<5 m<2 =
8 m<6
4.- los ángulos conjugadas externas son suplementarios:=
m<3 = m<7 m<4
m<8
m<1 + m<7 = 180º m<2 + m<8 = 180º
Regresar 5.- Los ángulos conjugadas internas son suplementarios:
Continuar m<3 + m<5 = 180º m<4 + m<6 = 180º

27. PROPIEDADES DE LOS ANGULOS
01.-Ángulos que se forman por una línea poligonal entre
dos rectas paralelas.
x
y
+ + = x + y

28. 02.- ÁNGULOS ENTRE DOS RECTAS PARALELAS
+ + + + = 180°

29. 03.- ÁNGULOS DE LADOS PERPENDICULARES
+ = 180°

31. Problema Nº 01
El complemento de la diferencia entre el suplemento
y el complemento de un ángulo “X” es igual al
duplo del complemento del ángulo “X”. Calcule la
medida del ángulo “X”.
RESOLUCIÓN
La estructura según el enunciado:
90 - { ( 180° - X ) - ( 90° - X ) } = 2( 90° - X )
Desarrollando se obtiene:
90° - { 180° - X - 90° + X } = 180° - 2X
90° - 90° = 180° - 2X
Luego se reduce a:
2X = 180° X = 90°

32. Problema Nº 02
La suma de las medidas de dos ángulos es 80° y el
complemento del primer ángulo es el doble de la medida
del segundo ángulo. Calcule la diferencia de las medidas de
dichos ángulos.
RESOLUCIÓN
Sean los ángulos: y
Dato: + = 80° = 80° - (1)
Dato: ( 90° - )=2 (2)
= 70°
Resolviendo
Reemplazando (1) en (2): = 10°
Diferencia de las medidas
( 90° - ) = 2 ( 80° - ) - = 70°-10°
90° - = 160° -2 = 60°

33. Problema Nº 03
La suma de sus complementos de dos ángulos es 130° y la
diferencia de sus suplementos de los mismos ángulos es
10°.Calcule la medida dichos ángulos.
RESOLUCIÓN
Sean los ángulos: y
Del enunciado:
( 90° - ) + ( 90° - ) = 130° + = 50° (+)
- = 10°
+ = 50° (1) 2 = 60°
Del enunciado:
( 180° - ) - ( 180° - ) = 10° = 30°
- = 10° (2)
= 20°
Resolviendo: (1) y (2)

34. Problema Nº 04
Se tienen ángulos adyacentes AOB y BOC (AOB<BOC), se
traza la bisectriz OM del ángulo AOC; si los ángulos BOC y
BOM miden 60° y 20° respectivamente. Calcule la medida
del ángulo AOB.
RESOLUCIÓN
De la figura:
A B
M = 60° - 20°
= 40°
X 20°
Luego:
60° X = 40° - 20°
X = 20°
O
C

35. Problema Nº 05
La diferencia de las medidas de dos ángulos adyacentes
AOB y BOC es 30°. Calcule la medida del ángulo formado
por la bisectriz del ángulo AOC con el lado OB.
RESOLUCIÓN Del enunciado:
Construcción de la gráfica según el
enunciado AOB - OBC = 30°
A
M ( + X) - ( - X) = 30º
B 2X=30º
Luego se reemplaza por lo que
X Se observa en la gráfica
( - X) X = 15°
O C

36. Problema Nº 06
Se tiene los ángulos consecutivos AOB, BOC y COD tal
que la m AOC = m BOD = 90°. Calcule la medida del
ángulo formado por las bisectrices de los ángulos AOB y
COD.
RESOLUCIÓN
Construcción de la gráfica según el enunciado
De la figura:
A M
B 2 + = 90°
(+)
+2 = 90°
C 2 +2 + 2 = 180°
X
+ + = 90°
X= + +
N
X = 90°
D

37. Problema Nº 07
Si m // n . Calcule la medida del ángulo “X”
m
80°
X
30° n

38. RESOLUCIÓN
m
80°
X
30° n
Por la propiedad 80° = + +X (2)
2 + 2 = 80° + 30° Reemplazando (1) en (2)
+ = 55° (1)
80° = 55° + X
Propiedad del cuadrilátero
cóncavo X = 25°

39. Problema Nº 08
Si m // n . Calcular la medida del ángulo “X”
m 4 65°
X
n
5

40. RESOLUCIÓN
m 4 65°
40° 65°
X
n
5
Por la propiedad: Ángulo exterior del triángulo
4 + 5 = 90° X = 40° + 65°
= 10° X = 105°

41. Problema Nº 09
Si m // n . Calcule la medida del ángulo ”X”
x
m
2
2
n

42. RESOLUCIÓN
x
m
2
2
n
Ángulos conjugados Ángulos entre líneas poligonales
internos
3 + 3 = 180°
+ = 60° X= + X = 60°