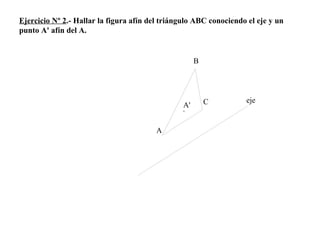
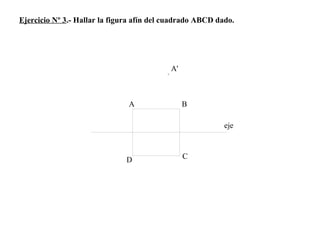
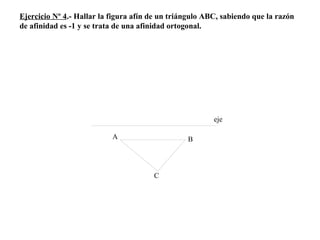
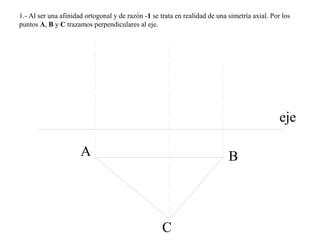
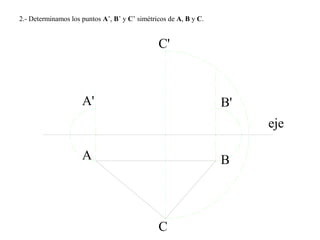
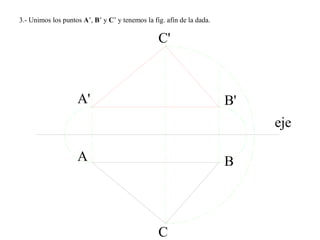
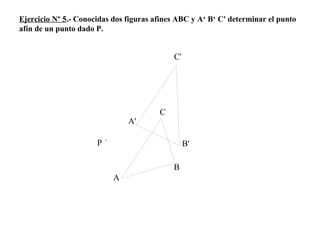
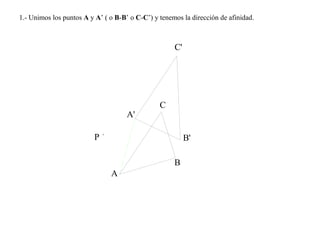
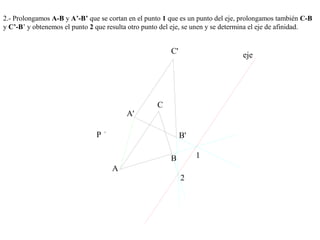
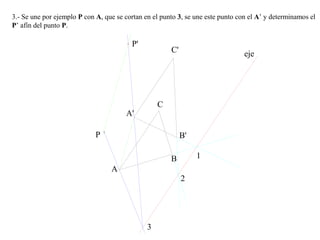
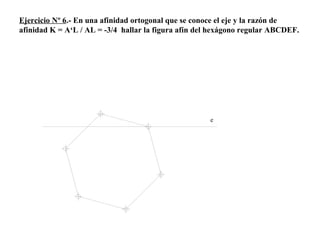
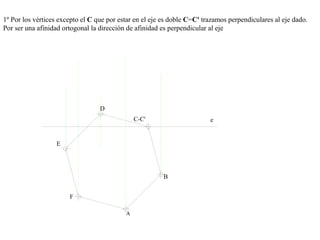
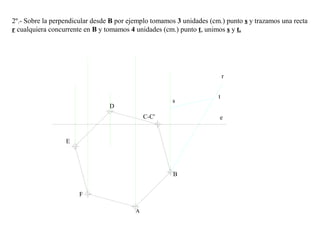
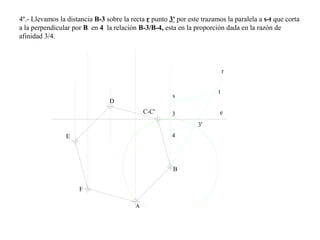
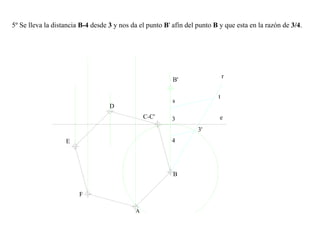
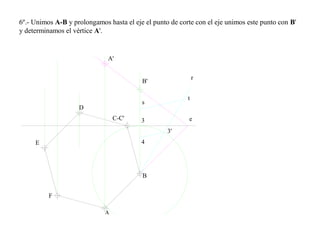
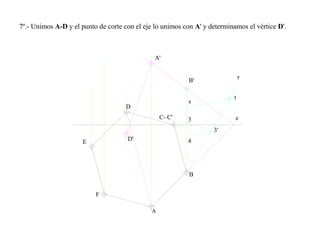
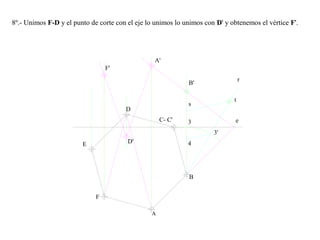
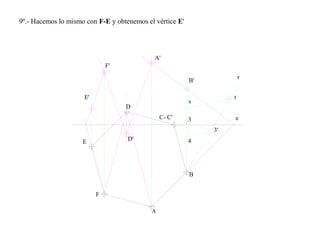
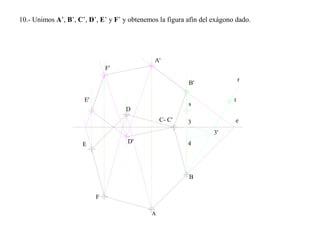
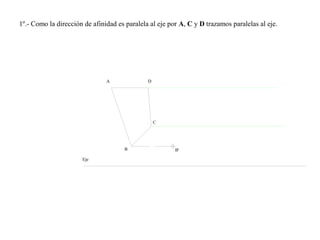
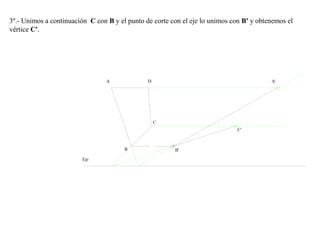
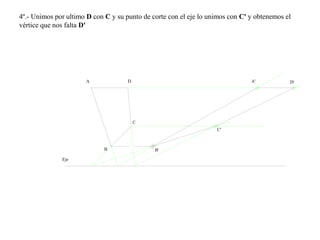
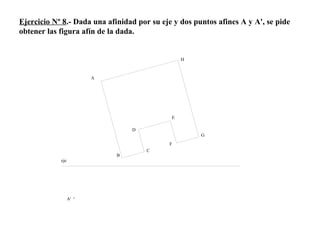
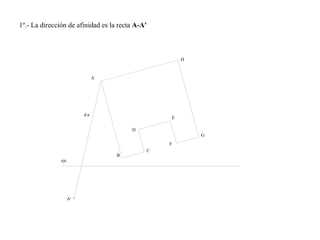
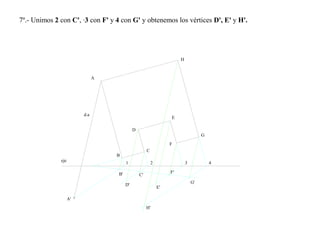
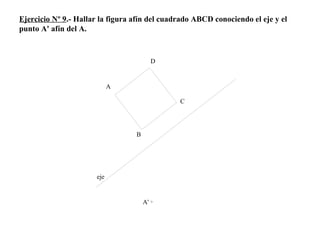
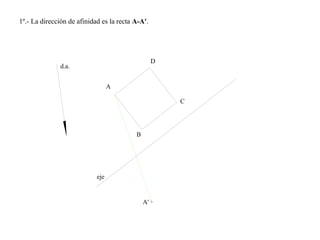
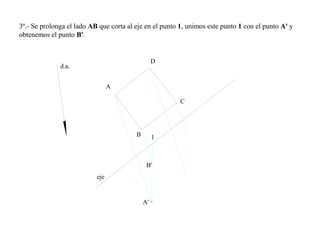
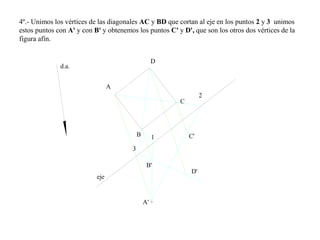
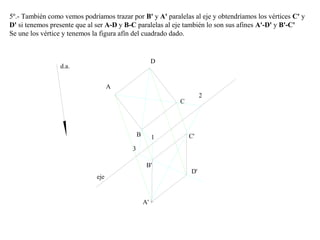
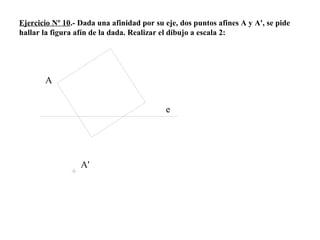
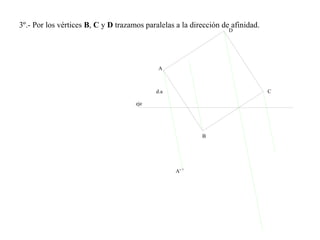
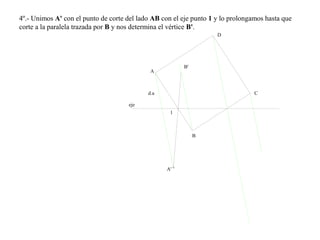
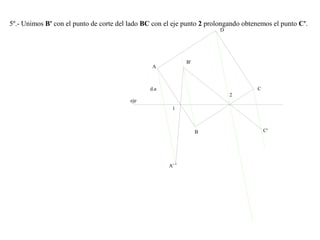
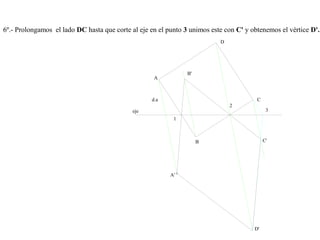
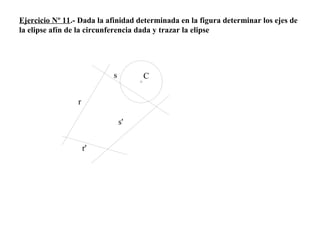
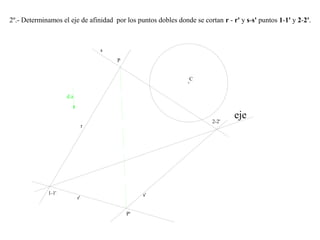
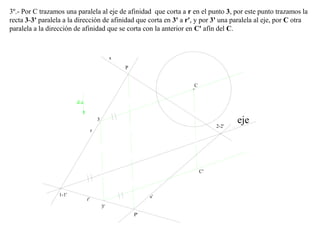
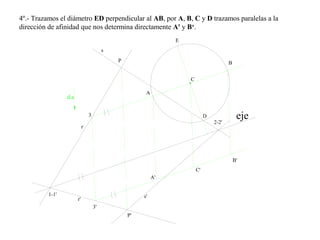
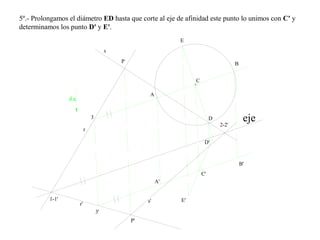
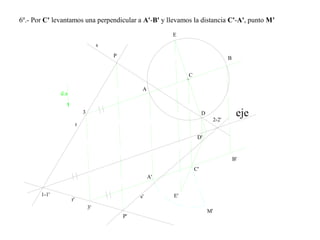
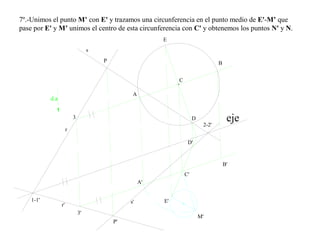
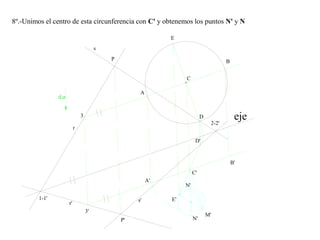
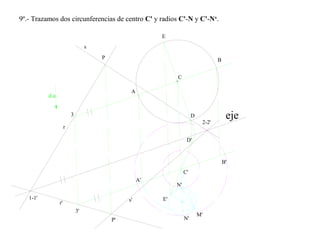
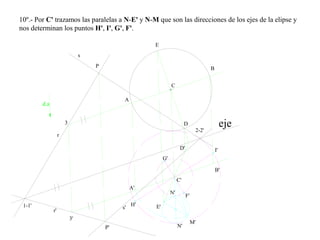
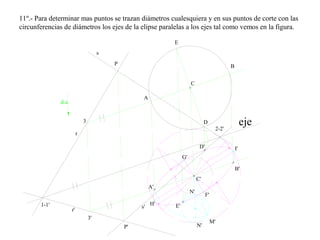
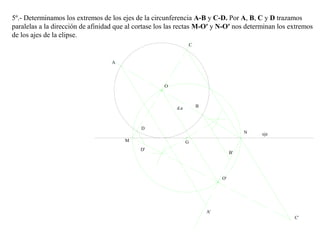
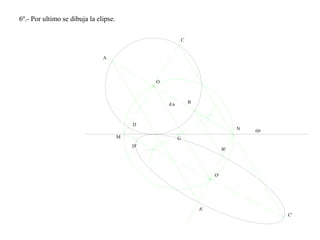
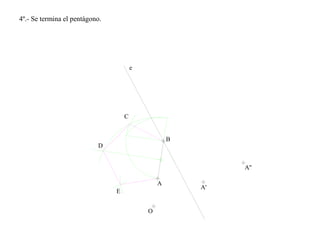
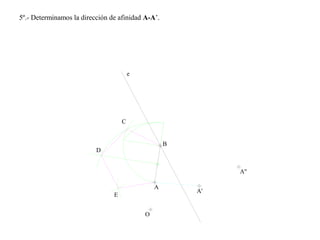
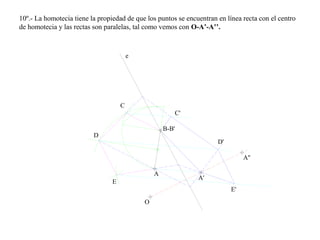
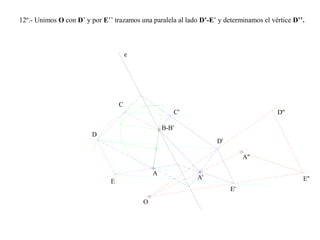
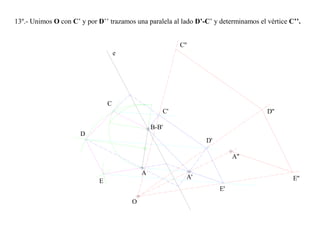
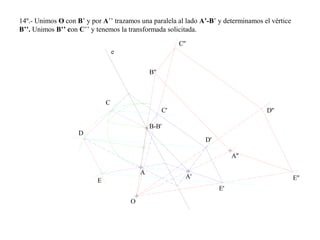
El documento presenta 10 ejercicios sobre transformaciones geométricas por afinidad. Explica cómo encontrar puntos, líneas y figuras afines dados un eje de afinidad y uno o más puntos afines de referencia. Los pasos incluyen trazar paralelas a la dirección de afinidad, prolongar líneas hasta el eje y unir puntos para determinar las figuras afines.

1. TRANSFORMACIONES
GEOMETRICAS
Afinidad

2. Ejercicio Nº 1.- Hallar el punto afín del B conociendo el eje de afinidad y un par
de puntos afines A y A'.
eje
A'
B
A

3. 1.- Tomamos un punto C cualquiera, por C trazamos una paralela a la dirección de afinidad A-A’, unimos A
con C y obtenemos el punto 1-1’, se une a continuación el punto 1-1’ con A’ y obtenemos el punto C’ afín del
C.
eje
A'
B
A
C
C'
1-1'

4. 2.- Una vez que tenemos el punto C-C’ de la misma afinidad que la dada. Unimos B con C y obtenemos el
punto 2-2’ que unido con C’ nos determina el punto B’ afín del B.
eje
A'
B
A
C
C'
1-1' 2-2'
B'

5. Ejercicio Nº 2.- Hallar la figura afín del triángulo ABC conociendo el eje y un
punto A' afín del A.
ejeC
A
B
A'

6. 1.- Unimos los puntos afines A y A’ y obtenemos la dirección de afinidad. Por B y C trazamos paralelas a esta
dirección A-A’
ejeC
A
B
A'

7. 2.- Unimos A y B y determinamos el punto 1-1’, unimos este con el A’ y obtenemos el punto B’ afín del B.
ejeC
A
B
A'
B'
1-1'

8. 3.- Unimos C y B y determinamos el punto 2-2’, unimos este con el B’ y obtenemos el punto C’ afín del C.
ejeC
A
B
A'
B'
1-1'
2-2'
C'

9. 4.- Unimos A’ C’ y B’ obtenemos la figura afín de la dada. También podríamos obtener el punto C
trazando una paralela por A’ al ser la recta A-C paralela al eje también lo es la afín A’-C’.
ejeC
A
B
A'
B'
1-1'
2-2'
C'

10. Ejercicio Nº 3.- Hallar la figura afín del cuadrado ABCD dado.
eje
A B
CD
A'

11. 1.- Determinamos la dirección de afinidad A-A’. Trazamos por los puntos B, C y D paralelas a la
recta A-A’.
eje
A B
CD
A'

12. 2.- Como la recta A-B es paralela al eje la recta afín A’-B’ será también paralela al eje, por tanto
por A’ trazamos la paralela a A-B y obtenemos B’.
eje
A B
CD
A' B'

13. 3.- Como la recta A-D y B-C cortan al eje las afines A’-B’ y B’-C’ cortaran al eje en el mismo punto. Se
une A’ y B’ con el punto donde A-D y B-C corta al eje y obtenemos los punto D’ y C’.
eje
A B
CD
A' B'
D' C'

14. 4.- Se unen los puntos A’,B’, C’ y D’ y obtenemos la figura afín de la fig. dada.
eje
A B
CD
A' B'
D' C'

15. Ejercicio Nº 4.- Hallar la figura afín de un triángulo ABC, sabiendo que la razón
de afinidad es -1 y se trata de una afinidad ortogonal.
eje
A B
C

16. 1.- Al ser una afinidad ortogonal y de razón -1 se trata en realidad de una simetría axial. Por los
puntos A, B y C trazamos perpendiculares al eje.
eje
A B
C

17. 2.- Determinamos los puntos A’, B’ y C’ simétricos de A, B y C.
eje
A B
C
B'
C'
A'

18. 3.- Unimos los puntos A’, B’ y C’ y tenemos la fig. afín de la dada.
eje
A B
C
B'
C'
A'

19. Ejercicio Nº 5.- Conocidas dos figuras afines ABC y A‘ B‘ C' determinar el punto
afín de un punto dado P.
C'
A
A'
P B'
B
C

20. 1.- Unimos los puntos A y A’ ( o B-B’ o C-C’) y tenemos la dirección de afinidad.
C'
A
A'
P B'
B
C

21. 2.- Prolongamos A-B y A’-B’ que se cortan en el punto 1 que es un punto del eje, prolongamos también C-B
y C’-B’ y obtenemos el punto 2 que resulta otro punto del eje, se unen y se determina el eje de afinidad.
C'
A
A'
P B'
B
C
eje
1
2

22. 3.- Se une por ejemplo P con A, que se cortan en el punto 3, se une este punto con el A’ y determinamos el
P’ afín del punto P.
C'
A
A'
P B'
B
C
eje
1
2
3
P'

23. Ejercicio Nº 6.- En una afinidad ortogonal que se conoce el eje y la razón de
afinidad K = A‘L / AL = -3/4 hallar la figura afín del hexágono regular ABCDEF.
e

24. 1º Por los vértices excepto el C que por estar en el eje es doble C=C' trazamos perpendiculares al eje dado.
Por ser una afinidad ortogonal la dirección de afinidad es perpendicular al eje
e
B
C-C'
D
E
F

25. 2º.- Sobre la perpendicular desde B por ejemplo tomamos 3 unidades (cm.) punto s y trazamos una recta
r cualquiera concurrente en B y tomamos 4 unidades (cm.) punto t, unimos s y t.
e
B
C-C'
D
E
F
s
t
r

26. 4º.- Llevamos la distancia B-3 sobre la recta r punto 3' por este trazamos la paralela a s-t que corta
a la perpendicular por B en 4 la relación B-3/B-4, esta en la proporción dada en la razón de
afinidad 3/4.
e
B
C-C'
D
E
F
s
t
3
3'
4
r

27. 5º Se lleva la distancia B-4 desde 3 y nos da el punto B' afín del punto B y que esta en la razón de 3/4.
e
B
C-C'
D
E
F
s
t
3
3'
4
B'
r

28. 6º.- Unimos A-B y prolongamos hasta el eje el punto de corte con el eje unimos este punto con B'
y determinamos el vértice A'.
e
B
C-C'
D
E
F
s
t
3
3'
4
B'
r

29. 7º.- Unimos A-D y el punto de corte con el eje lo unimos con A' y determinamos el vértice D'.
e
B
C- C'
D
E
F
s
t
3
3'
4
B'
D'
r

30. 8º.- Unimos F-D y el punto de corte con el eje lo unimos lo unimos con D' y obtenemos el vértice F'.
e
B
C- C'
D
E
F
s
t
3
3'
4
B'
F'
D'
r

31. 9º.- Hacemos lo mismo con F-E y obtenemos el vértice E'
e
B
C- C'
D
E
F
s
t
3
3'
4
B'
F'
E'
D'
r

32. 10.- Unimos A’, B’, C’, D’, E’ y F’ y obtenemos la figura afín del exágono dado.
e
B
C- C'
D
E
F
s
t
3
3'
4
B'
F'
E'
D'
r

33. Ejercicio Nº 7.- Trazar la figura afín del cuadrilátero ABCD donde se conoce B'
A
B B'
C
D
Eje

34. 1º.- Como la dirección de afinidad es paralela al eje por A, C y D trazamos paralelas al eje.
A
B B'
C
D
Eje

35. 2º.- Unimos A y B y prolongamos hasta el eje unimos el punto de corte con el eje con B' y
obtenemos el vértice A'.
A
B B'
C
D
Eje
A'

36. 3º.- Unimos a continuación C con B y el punto de corte con el eje lo unimos con B' y obtenemos el
vértice C'.
A
B B'
C
D
Eje
A'
C'

37. 4º.- Unimos por ultimo D con C y su punto de corte con el eje lo unimos con C' y obtenemos el
vértice que nos falta D'
A
B B'
C
D
Eje
A' D'
C'

38. Ejercicio Nº 8.- Dada una afinidad por su eje y dos puntos afines A y A', se pide
obtener las figura afín de la dada.
eje
A
A'
B
C
D
E
F
G
H

39. 1º.- La dirección de afinidad es la recta A-A'
eje
A
A'
B
C
D
E
F
G
H
d.a

40. 2º.- Por los vértices restantes B, C, D, E, F, G y H trazamos paralelas a la dirección de afinidad d.a.
eje
A
A'
B
C
D
E
F
G
H
d.a

41. 3º.- Prolongamos AB hasta el eje punto 1 unimos este con A' y nos determina el vértice B'.
eje
A
A'
B
C
D
E
F
G
H
1
B'
d.a

42. 4º.- Unimos B con G que pasa por C y F hasta que corte el eje por este punto unimos con B' y
obtenemos los vértices C', F' y G'
5º.- Unimos 2 con C', ·3 con F' y 4 con G' y obtenemos los vértices D', E' y H'.
6º.- Unimos los vértices y tenemos la figura afín de la dada
eje
A
A'
B
C
D
E
F
G
H
1
B' F'
C'
G'
d.a

43. 7º.- Unimos 2 con C', ·3 con F' y 4 con G' y obtenemos los vértices D', E' y H'.
eje
A
A'
B
C
D
E
F
G
H
1 2 3 4
B'
D'
E'
F'
C'
G'
H'
d.a

44. 8º.- Unimos los vértices y tenemos la figura afín de la dada
eje
A
A'
B
C
D
E
F
G
H
1 2 3 4
B'
D'
E'
F'
C'
G'
d.a

45. Ejercicio Nº 9.- Hallar la figura afín del cuadrado ABCD conociendo el eje y el
punto A' afín del A.
A
B
C
D
A'
eje

46. 1º.- La dirección de afinidad es la recta A-A'.
d.a.
A
B
C
D
A'
eje

47. 2º.- Por los vértices del cuadrado B, C, y D, se trazan las rectas paralelas a la dirección afinidad A-A'.
d.a.
A
B
C
D
A'
eje

48. 3º.- Se prolonga el lado AB que corta al eje en el punto 1, unimos este punto 1 con el punto A' y
obtenemos el punto B'.
d.a.
A
B
C
D
A'
B'
1
eje

49. 4º.- Unimos los vértices de las diagonales AC y BD que cortan al eje en los puntos 2 y 3 unimos
estos puntos con A' y con B' y obtenemos los puntos C' y D', que son los otros dos vértices de la
figura afín.
d.a.
A
B
C
D
A'
C'
D'
B'
1
2
3
eje

50. 5º.- También como vemos podríamos trazar por B' y A' paralelas al eje y obtendríamos los vértices C' y
D' si tenemos presente que al ser A-D y B-C paralelas al eje también lo son sus afines A'-D' y B'-C'
Se une los vértice y tenemos la figura afín del cuadrado dado.
d.a.
A
B
C
D
A'
C'
D'
B'
1
2
3
eje

51. Ejercicio Nº 10.- Dada una afinidad por su eje, dos puntos afines A y A', se pide
hallar la figura afín de la dada. Realizar el dibujo a escala 2:
e
A
A'

52. 1º.- Reproducimos los datos dados a la escala solicitada 2:1
A
A'
eje

53. 2º.- Determinamos la dirección de afinidad que es la recta A-A'.
d.a
A
A'
eje

54. 3º.- Por los vértices B, C y D trazamos paralelas a la dirección de afinidad.
d.a
A
A'
B
C
D
eje

55. 4º.- Unimos A' con el punto de corte del lado AB con el eje punto 1 y lo prolongamos hasta que
corte a la paralela trazada por B y nos determina el vértice B'.
d.a
A
A'
B'
B
C
D
eje
1

56. 5º.- Unimos B' con el punto de corte del lado BC con el eje punto 2 prolongando obtenemos el punto C'.
d.a
A
A'
B'
B
C
C'
D
eje
1
2

57. 6º.- Prolongamos el lado DC hasta que corte al eje en el punto 3 unimos este con C' y obtenemos el vértice D'.
d.a
A
A'
B'
B
C
C'
D
D'
eje
1
2
3

58. Ejercicio Nº 11.- Dada la afinidad determinada en la figura determinar los ejes de
la elipse afín de la circunferencia dada y trazar la elipse
r
s C
s'
r'

59. 1º.- La dirección de afinidad (d.a.) es la recta que une P y P' puntos donde se cortan r-s y r'-s'.
r'
s'
C
s
r
P
P'
d.a

60. 2º.- Determinamos el eje de afinidad por los puntos dobles donde se cortan r - r' y s-s' puntos 1-1' y 2-2'.
r'
s'
C
s
r
eje
P
P'
d.a
1-1'
2-2'

61. 3º.- Por C trazamos una paralela al eje de afinidad que corta a r en el punto 3, por este punto trazamos la
recta 3-3' paralela a la dirección de afinidad que corta en 3' a r', y por 3' una paralela al eje, por C otra
paralela a la dirección de afinidad que se corta con la anterior en C' afín del C.
r'
s'
C
s
r
eje
P
P'
d.a
C'
1-1'
2-2'
3
3'

62. 4º.- Trazamos el diámetro ED perpendicular al AB, por A, B, C y D trazamos paralelas a la
dirección de afinidad que nos determina directamente A' y B‘.
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
1-1'
2-2'
3
3'

63. 5º.- Prolongamos el diámetro ED hasta que corte al eje de afinidad este punto lo unimos con C' y
determinamos los punto D' y E'.
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'1-1'
2-2'
3
3'

64. 6º.- Por C' levantamos una perpendicular a A'-B' y llevamos la distancia C'-A', punto M’
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'
M'
1-1'
2-2'
3
3'

65. 7º.-Unimos el punto M’ con E' y trazamos una circunferencia en el punto medio de E'-M’ que
pase por E' y M’ unimos el centro de esta circunferencia con C' y obtenemos los puntos N' y N.
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'
M'
1-1'
2-2'
3
3'

66. 8º.-Unimos el centro de esta circunferencia con C' y obtenemos los puntos N' y N
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'
M'
N'
N'
1-1'
2-2'
3
3'

67. 9º.- Trazamos dos circunferencias de centro C' y radios C'-N y C'-N‘.
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'
M'
N'
N'
1-1'
2-2'
3
3'

68. 10º.- Por C' trazamos las paralelas a N-E' y N-M que son las direcciones de los ejes de la elipse y
nos determinan los puntos H', I', G', F'.
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'
M'
N'
N'
F'
G'
H'
I'
1-1'
2-2'
3
3'

69. 11º.- Para determinar mas puntos se trazan diámetros cualesquiera y en sus puntos de corte con las
circunferencias de diámetros los ejes de la elipse paralelas a los ejes tal como vemos en la figura.
r'
s'
C
s
r
eje
P
P'
d.a
C'
A
B
A'
B'
E
D
D'
E'
M'
N'
N'
F'
G'
H'
I'
1-1'
2-2'
3
3'

70. Ejercicio Nº 12.- Hallar la figura afín de la circunferencia dada sabiendo que el
punto afín del centro es el punto O'. Realizar el dibujo a escala 2:1
e
O
O'

71. 1º.-Dibujamos los datos a escala 2:1
eje
O
O'

72. 2º.- La dirección de afinidad es la recta O-O' que une los centros.
eje
O
O'
d.a

73. 3º.- Hallamos la mediatriz de O-O', donde esta corta al eje de afinidad punto G trazamos una
circunferencia de diámetro O-O', que corta al eje en los puntos M y N que son puntos de los ejes.
eje
O
O'
d.a
GM
N

74. 4º.- Unimos N y M con O y O' y estas rectas son los ejes perpendiculares de la elipse y de la
circunferencia.
eje
O
O'
d.a
A
B
C
D
GM
N

75. 5º.- Determinamos los extremos de los ejes de la circunferencia A-B y C-D. Por A, B, C y D trazamos
paralelas a la dirección de afinidad que al cortase los las rectas M-O' y N-O' nos determinan los extremos
de los ajes de la elipse.
eje
O
O'
d.a
A
B
C
D
G
C'
A'
D'
B'
M
N

76. 6º.- Por ultimo se dibuja la elipse.
eje
O
O'
d.a
A
B
C
D
G
C'
A'
D'
B'
M
N

77. Ejercicio Nº 13.- Obtener la figura transformada del pentágono regular ABCDE
de lado AB conocido, tras aplicarle primero una afinidad de eje e y conocido un
punto A' afín del A y posteriormente una homotecia de centro O y siendo A'' el
transformado de A'. Dibuja el pentágono regular a la izquierda del lado AB.
A
O
B
e
A'
A''

78. 2º.- Comenzamos por construir el pentágono regular como ya sabemos.
A
O
B
e
A'
A''

79. 3º.- Seguimos la construcción del pentágono.
A
O
B
e
A'
A''
E

80. 4º.- Se termina el pentágono.
A
O
B
e
A'
A''
C
D
E

81. 5º.- Determinamos la dirección de afinidad A-A’.
A
O
B
e
A'
A''
C
D
E

82. 6º.- Por los vértices C, D y E trazamos paralelas a la dirección de afinidad A-A’.
A
O
B
e
A'
A''
C
D
E

83. 7º.- Unimos E-A y prolongamos para que corte al eje y se une con A’ para determinar E’.
A
O
B-B'
e
A'
A''
C
D
E
E'

84. 8º.- Unimos D con A hasta que corte al eje y se une este punto del eje con A’ y nos determina D’.
A
O
B-B'
e
A'
A''
C
D
E
D'

85. 9º.- Prolongamos el lado D-C para que corte al eje y se une este punto del eje con D’ y nos
determina C’, como el punto B es un punto doble B-B’, tenemos la figura afín de la dada.
A
O
B-B'
A'
C
D
E
E'
C'
D'

86. 10º.- La homotecia tiene la propiedad de que los puntos se encuentran en línea recta con el centro
de homotecia y las rectas son paralelas, tal como vemos con O-A’-A’’.
A
O
B-B'
e
A'
A''
C
D
E
E'
C'
D'

87. 11º.- Unimos O con E’ y por A’’ trazamos una paralela al lado A’-E’ y determinamos el vértice E’’.
A
O
B-B'
A'
A''
C
D
E
E'
C'
D'
E''

88. 12º.- Unimos O con D’ y por E’’ trazamos una paralela al lado D’-E’ y determinamos el vértice D’’.
A
O
B-B'
e
A'
A''
C
D
E
E'
C'
D'
E''
D''

89. 13º.- Unimos O con C’ y por D’’ trazamos una paralela al lado D’-C’ y determinamos el vértice C’’.
A
O
B-B'
e
A'
A''
C
D
E
E'
C'
D'
E''
D''
C''

90. 14º.- Unimos O con B’ y por A’’ trazamos una paralela al lado A’-B’ y determinamos el vértice
B’’. Unimos B’’ con C’’ y tenemos la transformada solicitada.
A
O
B-B'
e
A'
A''
C
D
E
E'
C'
D'
E''
D''
C''
B''