El documento explica diferentes métodos de interpolación y aproximación polinómica, incluyendo interpolación cuadrática y de Newton, polinomios de Hermite, Laguerre, Legendre, Chebyshev, y aproximación de mínimos cuadrados. Proporciona ejemplos y soluciones detalladas para cada método.

1. ( ) ∑ ∏
( )
( )
( ) ( ( )) Dar puntos e interpolar.
Solución:
( )
( )
( )
Interpolación Cuadrática:
( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
( )
( )
Ejemplo 2: Hallar el polinomio cuadrático que interpola a en los nodos
, usar el polinomio para hallar y hallar una cota para el
error.
( )
( )( )
( )( )
( )( )
( )( )
( )( )
( )( )
( )
( )

2. ( ) ( )
( )( )( ) ( )
( )
( )
( ) (Derivada igual a cero)
( )
( ) ( )
( )
( )
( )
( )
( )
( ) ( )
Diferencias divididas: Polinomio de Newton
Ejemplo 1: Construir la tabla de diferencias divididas para ( ) ( )
i ( ) de 1 de 2 de 3 de 4
0 0.068485
1 0.270734 0.772534
2 0.578469 1.17546 0.769532
3 0.88967 1.1887 0.025287 -0.947602
4 0.624266 -0.506884 -2.15888 -2.08573 -0.869466
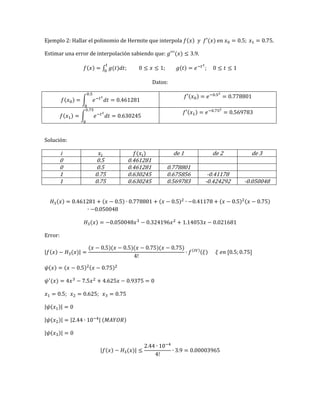
Ejemplo 2: Hallar el polinomio cúbico que interpola a ( ) ( ) en los nodos
; usar el polinomio para evaluar ( ), Hallar
una cota para el error en [0.5; 1.5].
i ( )
0 0.877583
1 0.731689 -0.583576
2 0.315322 -0.832734 -0.332211
3 0.070737 -0.97834 -1.194141 0.138061
( ) ( ) ( )( )
( )( )( )

3. ( )
( )
( ) ( )
( )( )( )( ) ( )
( )
( )
( )
( )
( ) ( )
( )
( )
( ( ))
( ) ( )
( )
( ( ))
( ) ( )
Polinomio de Hermite
Ejemplo 1: Hallar el polinomio que interpola a en
i ( ) de 1 de 2 de 3
0 0 1
0 0 1 ( )
1 1
1 1 e ( )
( ) ( ) ( ) ( )( )

4. Ejemplo 2: Hallar el polinomio de Hermite que interpola ( ) ( ) en .
Estimar una error de interpolación sabiendo que: ( ) .
( ) ∫ ( ) ; ; ( ) ;
Datos:
( ) ∫
( )
( ) ∫
( )
Solución:
i ( ) de 1 de 2 de 3
0 0.5 0.461281
0 0.5 0.461281 0.778801
1 0.75 0.630245 0.675856 -0.41178
1 0.75 0.630245 0.569783 -0.424292 -0.050048
( ) ( ) ( ) ( ) ( )
( )
Error:
( ) ( )
( )( )( )( ) ( )
( )
( ) ( ) ( )
( )
( )
( ) ( )
( )
( ) ( )

5. Aproximación discreta de mínimos cuadrados
Ejemplo 1:
i y( )
1 0 1 0 0
2 0.15 1.004 0.0225 0.1506
3 0.31 1.031 0.0961 0.31961
4 0.5 1.117 0.25 0.5585
5 0.6 1.223 0.36 0.7338
6 0.75 1.422 0.5625 1.0665
∑ ∑ ∑ ∑ ∑
Sistema de ecuaciones se resuelve mediante:
(∑ ) (∑ ) ∑
(∑ ) (∑ ) ∑
Recta de regresión lineal
Ejemplo 2:
i y( )
1 1 1.84 1 1 1 1.84 1.84
2 1.1 1.96 1.21 1.331 1.4641 2.156 2.3716
3 1.3 2.21 1.69 2.197 2.8561 2.873 3.7349
4 1.5 2.45 2.25 3.375 5.0625 3.675 5.5125
5 1.9 2.94 3.61 6.859 13.0321 5.586 10.6134
6 2.1 3.18 4.41 9.261 19.4481 6.678 14.0238
∑ ∑ ∑
14.17 24.023 42.8629 22.808 38.0962

6. Sistema de ecuaciones:
; ;
( )
Error de ajuste:
∑( ( ))
Polinomios de Legendre
( )
( ) ( )
( )
( )
( )
( )
( ) ( )
( ) ( )
∫ ( ) ( )
( ) ∑ ( )

7. ∫ ( ) ( )
Ejemplo 1:
Determinar el polinomio de aproximación por mínimos cuadrados de grado 3 en el intervalo
[-1,1] usando polinomios de Legendre de la función:
( ) ( ) ( )
Solución:
∫ ( )
∫ ( )
∫ ( ) ( )
∫ ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
Polinomios de Chebyshev
( )
√
( ) ( )
( ) ( )
( )
( )

8. ( )
( )
( )
∫
( ) ( )
√
( ) ∑ ( )
∫ ( ) ( )
Ejemplo 1:
Hallar la aproximación cúbica de mínimos cuadrados de la función ( ) ( ) en el
intervalo [1,3] usando polinomios de Chevyshev.
Solución:
( ) ( )
( ) ( ) ( ) ( )
∫
( ) ( )
√
∫
( ) ( )
√
∫
( ) ( ) ( )
√
∫
( ) ( ) ( )
√

9. ( ) ( ) ( ) ( )
( )
Polinomios de Laguerre
( )
( ) ( ) ( )
( )
( )
( )
( )
( )
∫ ( ) ( )
( )
( ) ∑ ( )
∫ ( ) ( )
Ejemplo 1:
Hallar el polinomio de aproximación de grado 3 de la función ( ) usando polinomios
de Laguerre.
Solución:
∫
∫ ( )
∫ ( )

10. ∫ ( )
( ) ( ) ( ) ( )
( )
Polinomios de Hermite:
( )
( ) ( ) ( )
( )
( )
( )
( )
( )
∫ ( ) ( )
√ ( )
( ) ∑ ( )
∫ ( ) ( )