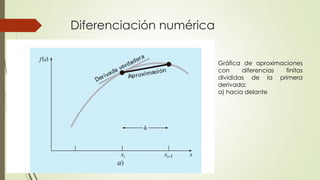
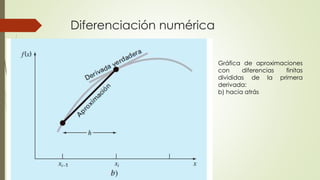
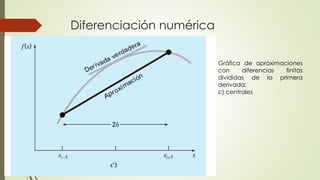
Este documento describe diferentes métodos numéricos para aproximar la derivada de una función, conocidos como diferencias finitas. Explica que la derivada puede aproximarse como la primera diferencia dividida hacia adelante, hacia atrás o central, con diferentes órdenes de error. También presenta un ejemplo numérico para ilustrar cómo aplicar estos métodos y calcular el error de las aproximaciones usando diferentes tamaños de paso.