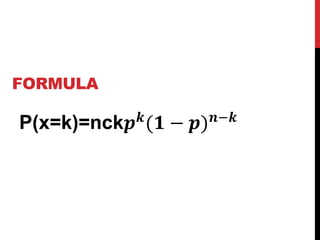Este documento resume conceptos básicos sobre distribuciones de probabilidad, en particular la distribución binomial. Explica la fórmula de la distribución binomial y proporciona ejemplos y problemas para ilustrar cómo se aplica la distribución binomial a situaciones que involucran múltiples ensayos de Bernoulli independientes y contar el número de éxitos. El documento concluye con cinco problemas para practicar el uso de la distribución binomial.

1. DISTRIBUCIONES DE
PROBABILIDADES
RAFAEL ARMANDO RAMÍREZ VILLARREAL
PROCESOS INDUSTRIALES ÁREA MANUFACTURA

2. CONTENIDO
Introducción.
Concepto básicos sobre p:
Binomial
Formula de p:
Binomial
Ejemplos y problemas para su mayor entendimiento sobre p:
binomial

3. INTRODUCCIÓN
Las probabilidades son muestras de una población
para analizar sus datos con el propósito de
aprender la inferencia estadística consiste en
extraer una muestra de una población y analizar
sus datos algunas de estas funciones comunes y las
condiciones en que es apropiado utilizar cada una

4. DISTRIBUCIÓN BINOMIAL
en la práctica, es posible extraer varios componentes de una gran
población y contar el número de elementos defectuosos. Esto implica
realizar diversos ensayos de Bernoulli independientes y contar el
número de éxitos. El número de éxitos es una variable aleatoria, que
tiene una distribución binomial

5. FORMULA
P(x=k)=nck𝒑 𝒌(𝟏 − 𝒑) 𝒏−𝒌

6. EJEMPLOS
Se lanza al aire diez veces una moneda. Sea X el número de caras que
aparecen. ¿Cuál es la
distribución de X?
Solución
Hay diez ensayos de Bernoulli independientes, cada uno con
probabilidad de éxito de p 0.5.
La variable aleatoria X es igual al número de éxitos en los diez ensayos.
Por consiguiente,
X Bin(10, 0.5).

7. EJEMPLO 2
Un lote contiene varios miles de componentes, de éstos 10% están
defectuosos. Se extraen
siete componentes de la población. Sea X el número de componentes
defectuosos en la muestra.
¿Cuál es la distribución de X?
Solución
Puesto que el tamaño muestral es pequeño en comparación con la
población (es decir, menor
a 5%), su número de éxitos representa una distribución binomial. Por
tanto, se modela X con
la distribución binomial Bin(7, 0.1).

8. EJEMPLO 3
Se lanza al aire ocho veces un dado. Determine la probabilidad de que
no salgan más de dos
números seis.
Solución
Cada lanzamiento del dado es un experimento Bernoulli con una
probabilidad de éxito de 1/6.
Sea X el número de seises en los ocho lanzamientos. Entonces X Bin(8,
1/6). Se necesita
determinar a P(X 2). Con el uso de la función de masa de probabilidad,

9. PROBLEMA 1
Se lanza una moneda cuatro veces. Calcular la probabilidad de que
salgan más caras que cruces

10. PROBLEMA 2
Si de seis a siete de la tarde se admite que un número de teléfono de
cada cinco está comunicando, ¿cuál es la probabilidad de que, cuando
se marquen 10 números de teléfono elegidos al azar, sólo comuniquen
dos?

11. PROBLEMA 3
La probabilidad de que un hombre acierte en el blanco es 1/4. Si
dispara 10 veces ¿cuál es la probabilidad de que acierte exactamente en
tres ocasiones? ¿Cuál es la probabilidad de que acierte por lo menos en
una ocasión?

12. PROBLEMA 4
Un agente de seguros vende pólizas a cinco personas de la misma edad
y que disfrutan de buena salud. Según las tablas actuales, la
probabilidad de que una persona en estas condiciones viva 30 años

13. PROBLEMA 5
La última novela de un autor ha tenido un gran éxito, hasta el punto de
que el 80% de los lectores ya la han leído. Un grupo de 4 amigos son
aficionados a la lectura: