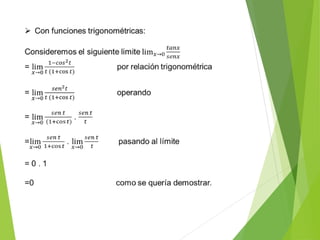
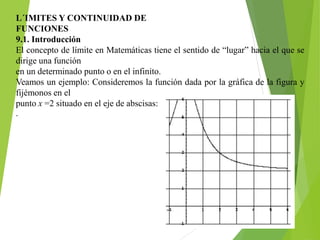
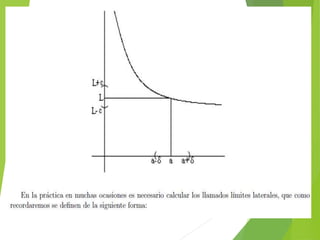
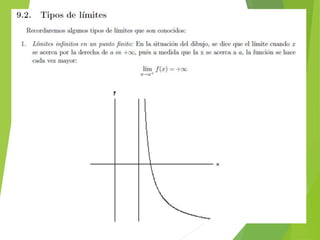
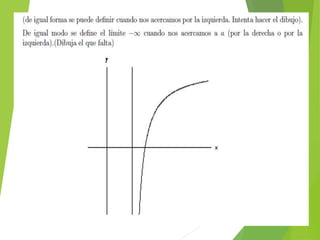
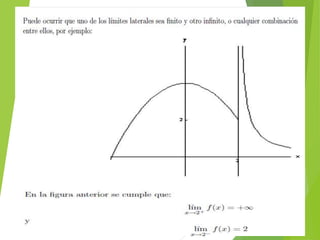
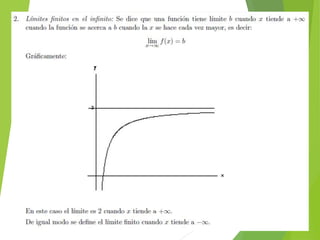
El documento trata sobre los conceptos de límites de sucesiones y funciones. Explica la idea intuitiva del límite de una sucesión como un valor al que se aproximan los términos de la sucesión, aunque no se alcance exactamente. Luego define formalmente la noción de límite de una sucesión y distingue entre sucesiones convergentes, que tienen un límite finito, y sucesiones divergentes, que no lo tienen. Finalmente, introduce conceptos sobre límites de funciones y cálculo de límites al infinito.
2. LIMITES Y SUCESIONES
Límite de una sucesión
Idea intuitiva del límite de una sucesión
En la sucesión an = 1/n, observamos que los términos se van acercando a cero.
Consideremos que 0 es el límite de la sucesión porque:
1 Los términos se aproximan a cero tanto como se quiera a medida que se avanza en
la sucesión.
2La distancia a cero puede ser tan pequeña como queramos.
d(1, 0) = 1
d(1/10, 0) = 0.1
d(1/100, 0) = 0.01
d(1/1000, 0) = 0.001
...
d(1/1 000 000, 0) = 0.000 001
...
d(1/1 000 000 000, 0) = 0.000 000 001
Vemos que el límite es 0 , pero no hay ningún valor de la sucesión que coincida con el
límite.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18. L´IMITES Y CONTINUIDAD DE
FUNCIONES
9.1. Introducción
El concepto de límite en Matemáticas tiene el sentido de “lugar” hacia el que se
dirige una función
en un determinado punto o en el infinito.
Veamos un ejemplo: Consideremos la función dada por la gráfica de la figura y
fijémonos en el
punto x =2 situado en el eje de abscisas:
.
33. LIMITE DE UNA SUCESION
El límite de una sucesión es uno de los
conceptos más antiguos del análisis
matemático. El mismo da una
definición rigurosa a la idea de una
sucesión que se va aproximando hacia
un punto llamado límite. Si una
sucesión tiene límite, se dice que es
una sucesión convergente, y que la
sucesión converge o tiende al límite.
En caso contrario, la sucesión es
divergente.
34. Sucesión convergente
- Tiene Limite finito
- Se puede ser hacer la suma de todos sus términos dentro de los reales.
Sucesión divergente
- No tiene limite al infinito real
- No se puede hacer la suma de todos sus términos, n debe estar definida.
