1) El documento explica el concepto geométrico de la derivada como la pendiente de la recta tangente a una curva en un punto. 2) Se define la derivada de una función f(x) como el límite de la pendiente de la secante a medida que el punto Q se acerca a P. 3) La derivada numéricamente es igual a la tasa de cambio promedio de la función en un intervalo e indica cómo varía la función cerca de ese punto.

1. INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA
En el cálculo se desarrollan dos grandes ideas cuyo fundamento se
encuentra en el límite de las funciones. En este tema abordaremos el concepto
de derivada, asociado a la comparación de dos variables relacionadas.
El concepto derivada de una función surge de manera simultánea en el
pensamiento de dos grandes figuras de la matemática del siglo XVII: Isaac
Newton y Gottfried Nilhelm Leibnitz. Este término es generado al intentar
resolver dos problemas, en apariencia sin relación alguna. Pero que sin
embargo son resueltos con idéntica fundamentación. El primero de ellos es de
carácter físico y geométrico y lo plantearemos en forma de pregunta.
Dada una curva ¿Cómo hallar la recta tangente a ella en un punto dado?
Desde luego, es necesario comprender el significado exacto de las
palabras que forman la pregunta, para intentar contestarla. Primeramente,
¿Qué es lo que viene a tu mente con referencia a la palabra tangente?
Recordarás haberlo empleado con relación a una circunferencia, como aquella
recta que “toca” un solo punto de esta.
Tangente
Figura 1
Secante
De la misma manera, la
secante de la circunferencia
corresponde a una recta que
“corta” a ésta, compartiendo
dos puntos con ella. Figura
1.

2. Es necesario modificar las concepciones que se tienen para secante y
tangente, si estas corresponden a las curvas abiertas, como es el caso de
aquellas que están asociadas a las funciones.
y
l2
Figura 2 l1 l3
l4
a b c d x
y
Tangente
Secante
x
Figura 3
La determinación de la tangente a una curva, en un punto dado, se logra
mediante la aproximación de un caso extremo, es decir, el límite. Considere la
Figura 4. En ella se ilustra una recta secante que pasa por los puntos P y Q, de
coordenadas.
P (x0, f (x0)), Q (x0 + x, f(x0 + x))
y Q
y = f (x)
P
x
x0 x0 + x
En la Figura 2 l1, l2,
l3 y l4 corresponden a la
tangente en distintos
puntos de la curva. Sin
embargo, la tangente en
un punto puede cortar la
curva en otro, y poseer
un doble papel: tangente
en un punto y secante
para otro. Figura 3.
Se sabe que la
pendiente m de la recta que
pasa por P y Q es:
00
0
)(
)()(
xxx
xfxxf
m



x
xfxxf
m



)()( 0
Figura 4

3. y
P
Q1
Q2
Q3
x
Figura 5
Evidentemente aquella que pasa por P y Q3, ya que este último punto es
el más cercano a P siguiendo este mismo razonamiento.
“Conforme un punto Q de la curva está más próximo a P, la
pendiente de la secante que pasa por P y Q será un valor más cercano a
la pendiente de la recta tangente de la curva en P”.
Lo anterior se verifica si: “la diferencia de las abscisas entre dos puntos
tienden a cero”. Dicho de otra manera:
Definición:
Por lo tanto: El significado geométrico de la derivada es la siguiente:
“La derivada de una función f(x) para un argumento x, es
numéricamente igual a la pendiente de la recta tangente a la curva
dada por la función en el punto (x, f(x))”.
Observa ahora la
Figura 5. ¿Cuál de las 3
secantes que se ilustran, se
asemeja más a la tangente
de la curva en P?
La pendiente m de la recta tangente a una curva dada por una función f,
en un punto de abscisa x, es:
x
xfxxf
m
x 



)()(
lím
0
Como x
y
xf


 )(
, tenemos que
)(xfm 
(x)'f=mquetenemosy/ x,=(x)'fComo
dpuntounenf,funciónunapordadaunacadacurvaunaatangenterectaladempendienteLa
)(
x
y
xf



f ' (x) = y
/x, tenemos que m = f '(x)

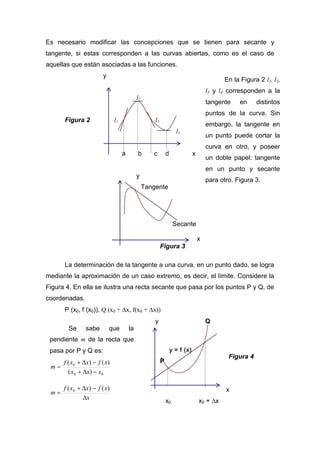
4. DERIVADA DE UNA FUNCIÓN.
Definición:
La razón
x
xfxxf
xencambio
yencambio
x
y




 )()(
, se denomina tasa de
cambio o razón de cambio promedio de la función en el intervalo entre x y
x+Δx.
Derivada de una función: Sea f una función continúa y suave en un intervalo
[a, b], si x es un punto del intervalo, entonces la derivada de la función en tal
punto se representa por f '(x) y la definimos como:
x
y
lím
x
xfxxf
límxf
xx 





 00
)()(
)(