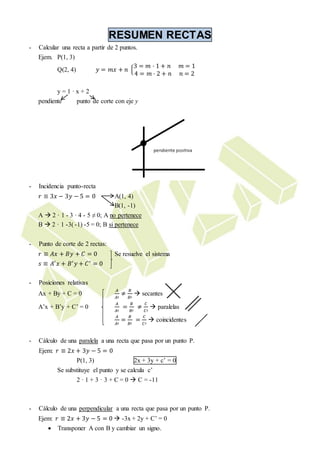
Este documento resume diferentes conceptos relacionados con rectas en el plano. Explica cómo calcular una recta a partir de dos puntos, determinar si un punto pertenece a una recta dada, encontrar el punto de intersección de dos rectas, y clasificar las posiciones relativas de dos rectas. También describe cómo calcular una paralela y una perpendicular a una recta dada, así como la distancia entre un punto y una recta. Por último, resume los conceptos de ángulo entre rectas, y rectas notables como la mediana, mediatriz y altura de un triá

1. RESUMEN RECTAS
- Calcular una recta a partir de 2 puntos.
Ejem. P(1, 3)
Q(2, 4) 푦 = 푚푥 + 푛 {
3 = 푚 · 1 + 푛 푚 = 1
4 = 푚 · 2 + 푛 푛 = 2
y = 1 · x + 2
pendiente punto de corte con eje y
- Incidencia punto-recta
푟 ≡ 3푥 − 3푦 − 5 = 0 A(1, 4)
B(1, -1)
A  2 · 1 - 3 · 4 - 5 ≠ 0; A no pertenece
B  2 · 1 -3( -1) -5 = 0; B si pertenece
- Punto de corte de 2 rectas:
푟 ≡ 퐴푥 + 퐵푦 + 퐶 = 0 Se resuelve el sistema
푠 ≡ 퐴′ 푥 + 퐵′푦 + 퐶 ′ = 0
- Posiciones relativas
Ax + By + C = 0
퐴
퐴′
≠ 퐵
퐵′
 secantes
A’x + B’y + C’ = 0
퐴
퐴′
= 퐵
퐵′
≠ 퐶
퐶′
 paralelas
퐴
퐴′
= 퐵
퐵′
= 퐶
퐶′
 coincidentes
- Cálculo de una paralela a una recta que pasa por un punto P.
Ejem: 푟 ≡ 2푥 + 3푦 − 5 = 0
P(1, 3) 2x + 3y + c’ = 0
Se substituye el punto y se calcula c’
2 · 1 + 3 · 3 + C = 0  C = -11
- Cálculo de una perpendicular a una recta que pasa por un punto P.
Ejem: 푟 ≡ 2푥 + 3푦 − 5 = 0  -3x + 2y + C’ = 0
 Transponer A con B y cambiar un signo.

2.  Calcular C’ como en el apartado anterior.
- Distancia punto-recta:
푑 (푃, 푟) =
퐴푥0 + 퐵푦0 + 퐶
√퐴2 + 퐵2
- Ángulo entre dos rectas:
Ax + By + C = 0  푢⃗ (−퐵, 퐴)
A’x + B’y + C’ = 0  푣 (−퐵′, 퐴′)
- Rectas “notables” de un triángulo
Ax + By + C = 0
P (x0 + y0)
 푐표푠푥 = 푢⃗⃗ ·푣⃗
|푢⃗⃗ |· |푣⃗ |
o Mediana: Pasa por un vértice y el punto medio del lado opuesto:
푃 · 푚 = (
푥1 + 푥2
2
,
푦1 + 푦2
2
)
o Mediatriz: Perpendicular por el punto medio
o Altura: Perpendicular a un lado que pasa por el vértice opuesto.