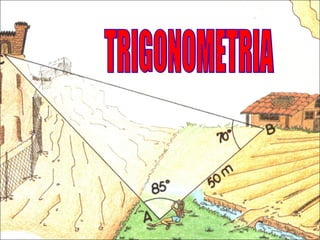
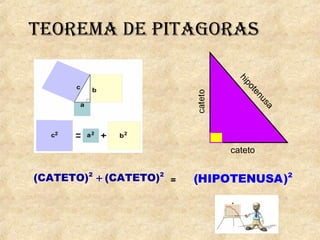
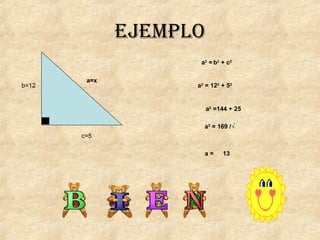
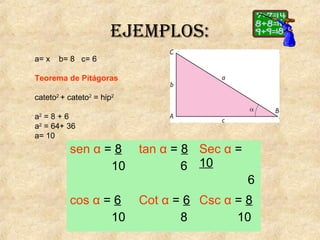
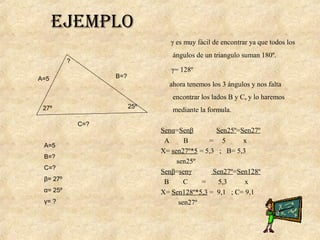
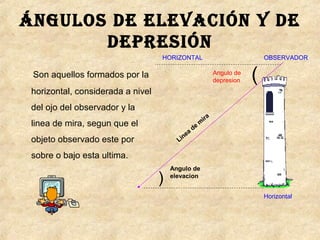
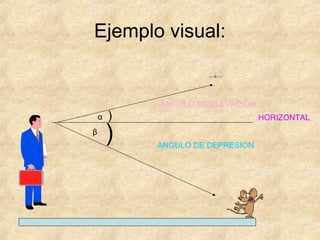
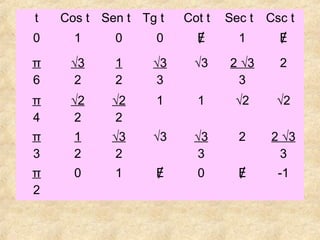
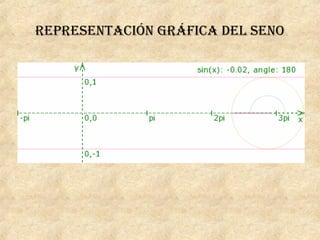
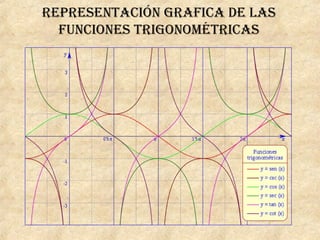
La trigonometría estudia las relaciones entre los ángulos y los lados de los triángulos. Incluye funciones como seno, coseno y tangente. Pitágoras descubrió el teorema que relaciona los catetos y la hipotenusa de un triángulo rectángulo. Las leyes del seno y coseno permiten resolver problemas de triángulos. Los ángulos de elevación y depresión miden la posición de objetos sobre o debajo de la horizontal.

2. TrigonomeTría:
• La trigonometría es la rama de las matemáticas cuyo significado etimológico es “la
medición de los triángulos”.
• Es la rama de las matemáticas que estudia la relación entre los ángulos y los lados
del triangulo.
• En términos generales es el estudio de las funciones seno, coseno, tangente,
cotangente, secante, cosecante. Que son aplicadas en todos aquellos ámbitos en los
que se requieren medidas de precisión.

3. PiTágoras de samos.
(aproximadamente 582 a. c. - 507 a. C.)
Fue un filósofo y matemático griego, famoso
sobre todo por el Teorema de Pitágoras.
Afirmaba que todo es matemáticas, y
estudió y clasificó los números.

4. Teorema de PiTagoras
2 2
(CATETO) (CATETO)+ 2
(HIPOTENUSA)=
cateto
hipotenusa

5. eJemPLo
b=12
c=5
a=x
a2
= b2
+ c2
a2
= 122
+ 52
a2
=144 + 25
a2
= 169 /√
a = 13

6. raZones TrigonomeTriCas.
Seno
SEN α = CATETO OPUESTO α
HIPOTENUSA
Coseno
COS α= CATETO ADYACENTE α
HIPOTENUSA
Tangente
Tan α= CATETO OPUESTO α
CATETO ADYACENTE α
Cotangente
Cot α= CATETO ADYACENTE α
CATETO OPUESTO α
Secante
Sec α= HIPOTENUSA
CATETO ADYACENTE α
Cosecante
Csc α= HIPOTENUSA
CATETO OPUESTO α

7. EjEmplos:
a= x b= 8 c= 6
Teorema de Pitágoras
cateto2
+ cateto2
= hip2
a2
= 8 + 6
a2
= 64+ 36
a= 10
sen α = 8
10
tan α = 8
6
Sec α =
10
6
cos α = 6
10
Cot α = 6
8
Csc α = 8
10

8. RazonEs tRigonomEtRicas
REcipRocas.
1 = sec α
Cos α
1 = csc α
Sen α
1 = cot α
tan α
Cos α sec α = 1 Sen α csc α = 1 Tan α cot α = 1
Ejemplos:
1 = sec 30º
Cos 30º
Csc 60º = 1
sen 60º
Tan 45º = 1
cos 45º

9. lEy dEl sEno
Senα = senβ + senγ
A B C
La ley de los Senos es una relación de tres igualdades que
siempre se cumplen entre los lados y ángulos de un triángulo
cualquiera, y que es útil para resolver ciertos tipo de problemas
de triángulos.
β
γ
α
B
C
A

10. EjEmplo
A=5 B=?
C=?
27º 25º
?
γ es muy fácil de encontrar ya que todos los
ángulos de un triangulo suman 180º.
γ= 128º
ahora tenemos los 3 ángulos y nos falta
encontrar los lados B y C, y lo haremos
mediante la formula.
Senα=Senβ Sen25º=Sen27º
A B = 5 x
X= sen27º*5 = 5,3 ; B= 5,3
sen25º
Senβ=senγ Sen27º=Sen128º
B C = 5,3 x
X= Sen128º*5,3 = 9,1 ; C= 9,1
sen27º
A=5
B=?
C=?
β= 27º
α= 25º
γ= ?

11. lEy dEl cosEno
C2
= A2
+ B2
– 2ABcosγ
β α
γ
A B
C
La ley de los Coseno es una
expresión que te permite conocer
un lado de un triángulo
cualquiera, si conoces los otros
dos y el ángulo opuesto al lado
que quieres conocer. Esta
relación es útil para resolver
ciertos tipos de problemas de
triángulos

12. EjEmplo.
Reemplazando en la formula nos queda que:
Que A =5,4071.
De ahí en adelante con el valor de A podemos
encontrar las demás incógnitas que faltan
por calcular mediante la ley del seno, donde
nos quedan los siguientes resultados:
senβ=0.7034297712, ahora invertir, y queda
sen-1 (0.7034297712),
β= 44. 703 = 44° 42'
ahora es muy fácil de encontrar el ultimo dato, solo
hay que estarle a 180º el valor de α y β:
γ= 180° -25°- 44°42' = 180° - 69°42' = 110°17'
γ= 110°17'
A=?
B=9
C=12
α=25º
β=?
γ= ?
A=? B=9
C=12
?
?
25º

13. Ángulos de elevación y de
depresión
Son aquellos formados por la
horizontal, considerada a nivel
del ojo del observador y la
linea de mira, segun que el
objeto observado este por
sobre o bajo esta ultima.
Linea
de
m
ira
)
Angulo de
elevacion
HORIZONTAL OBSERVADOR
(Angulo de
depresion
Horizontal

14. definición:
• Definición Angulo de Elevación.
Si un objeto esta por encima de la
horizontal, se llama Angulo de
elevación al Angulo formado por una
línea horizontal y la línea visual hacia
el objeto.
Definición Angulo de Depresión.
Si un objeto esta por debajo de la
horizontal, se llama Angulo de
depresión al Angulo formado por una
línea horizontal y la línea visual hacia
el objeto.

15. Ejemplo visual:
HORIZONTAL
ANGULO DE ELEVACION
ANGULO DE DEPRESION
)
)β
α

16. La distancia de un observador a la azotea de un edificio es de 169 metros
y el angulo de elevacion que se forma es 24. Hallar la distancia del
observador a la base del edificio.
Ejemplos:
Solucion.
Usaremos la relacion coseno:
cos 24º = x
169
x = 169 cos 24º
x = 154
La distancia buscada es de 154 metros
aproximadamente.
azotea
169m.
observadorbase x
edificio

17. Angulo de depresion:
Desde lo alto de un faro, cuya altura sobre el nivel del mar es de 120 metros, el Angulo de
depresión de una embarcación es de 15º. ¿A que distancia del faro esta la embarcación ?
Solución.
Lo primero que tenemos que hacer es dibujar el triangulo que se forma
con los datos del problema.
Aunque el problema viene con un angulo de
depresion de 15, por la nota anterior el
angulo de elevación mide lo mismo. A partir de
aquı hacemos uso de la relacion tangente:
tan 15º =120
x
x =120 tan 15º
x = 448
Respuesta: la distancia del barco al faro
es entonces, aproximadamente de 448 metros.
Angulo de depresion= 15º
15º
120 m.
x
)

18. funciones trigonométricas:
• Las funciones trigonométricas son igualdades que involucran las
funciones trigonométricas, verificables para cualquier valor que
tome la variable.

19. t Cos t Sen t Tg t Cot t Sec t Csc t
0 1 0 0 Ɇ 1 Ɇ
π
6
√3
2
1
2
√3
3
√3 2 √3
3
2
π
4
√2
2
√2
2
1 1 √2 √2
π
3
1
2
√3
2
√3 √3
3
2 2 √3
3
π
2
0 1 Ɇ 0 Ɇ -1

20. RepResentación gRáfica del seno

21. RepResentación gRafica de las
funciones tRigonométRicas

22. ejemplos
Cos π
12
• Determinar
Cos π - π
3 4
= 1 . √2 + √3 . √2
2 2 2 2
= √2 + √6
4 4
= √2 1 + √3
4
= cos π . cos π + sen π . Sen π
3 4 3 4

23. BiBliogRafia
• http://www.scribd.com/doc/198857/Ley-del-seno-y-ley-del-coseno
• http://www.monografias.com/trabajos13/trigo/trigo.shtml#cose
• http://www.hispanosnet.com/paginas/gif_animados.html
• http://es.wikipedia.org/wiki/Trigonometr%C3%ADa
•

24. INTEGRANTES:
CLAUDIA ANDREA ROJAS LLAITUL
BARBARA CATALINA ROJAS OJEDA
DANIELA ALEJANDRA MILLAPAN REYES
GRACIAS POR SU ATENCION