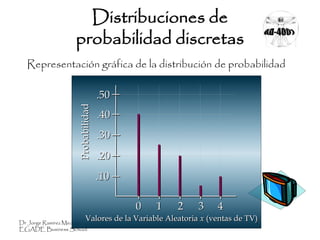
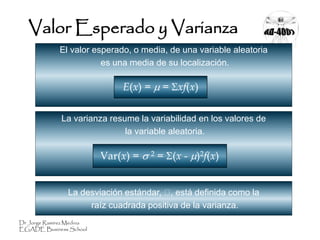
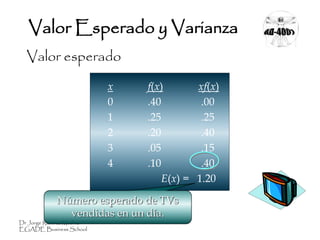
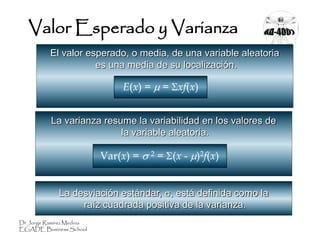
Este documento presenta conceptos clave sobre distribuciones de probabilidad. Explica que una variable aleatoria puede ser discreta o continua, dependiendo de si puede asumir valores finitos o infinitos. También define la función de probabilidad y cómo esta describe la distribución de probabilidad de una variable aleatoria. Por último, introduce las medidas de valor esperado y varianza para resumir las características de una distribución.

1. Sesión 2
Distribuciones de probabilidad
Estadística en las organizaciones
AD4001
Dr. Jorge Ramírez Medina

2. Dr Jorge Ramírez Medina
EGADE Business School
Variable aleatoria
Una variable aleatoria es una descripción numérica
del resultado de un experimento.
Una variable aleatoria discreta puede asumir un
número finito de valores o una secuencia infinita de
Valores.
Una variable aleatoria continua puede asumir
cualquier valor numérico en una intervalo o un
conjunto de intervalos.

3. Dr Jorge Ramírez Medina
EGADE Business School
Tome x = número de TVs vendidas en la tienda
en un día. x puede tomar 5 valores (0, 1, 2, 3, 4)
Ejemplo: Tiendas de Todo
Variable aleatoria discreta con un número
finito de valores.

4. Dr Jorge Ramírez Medina
EGADE Business School
Variable aleatoria discreta con un número
infinito de valores.
Podemos contar los clientes pero no hay un
límite finito de los que puedan llegar.
Tome x = número de clientes que llegan a la tienda
en un día. x puede tomar 5 valores 0, 1, 2, 3, 4…..
Ejemplo: Tiendas de Todo

5. Dr Jorge Ramírez Medina
EGADE Business School
Pregunta Random Variable x Type
Tamaño de
La familia
x = Número of dependientes
reportados para el censo
Discreta
Distancia de la
casa a la escuela
x = Distancia en kms. de la
casa a la escuela
Continua
Tener mascota
perros y/o
gatos
x = 1 si no tiene mascota;
= 2 si tiene perro(s) únicamente;
= 3 si tiene gato(s) únicamente;
= 4 si tiene perro(s) y gatos(s)
Discreta
Variables aleatorias

6. Dr Jorge Ramírez Medina
EGADE Business School
La distribución de probabilidad de una variable
aleatoria describe como las probabilidades están
distribuidas sobre los valores de la variable.
Podemos representar la distribución discreta de
probabilidad con una tabla, una gráfica o una ecuación.
Distribuciones de
probabilidad discretas

7. Dr Jorge Ramírez Medina
EGADE Business School
La distribución de probabilidad está definida por una función
de probabilidad, f(x), la cuál provee la probabilidad para
cada valor de la variable aleatoria.
Las condiciones requeridas para una función de
Probabilidad discreta son;
f(x) > 0
f(x) = 1
Distribuciones de
probabilidad discretas

8. Dr Jorge Ramírez Medina
EGADE Business School
desarrolle una representación tabular de la distribución
de probabilidad de las ventas de TVs
Utilizando los datos de ventas de TV’s
Unidades Número
Vendidas de días
0 80
1 50
2 40
3 10
4 20
200
x f(x)
0 .40
1 .25
2 .20
3 .05
4 .10
1.00
80/200
Distribuciones de
probabilidad discretas

9. Dr Jorge Ramírez Medina
EGADE Business School
.10
.20
.30
.40
.50
0 1 2 3 4
Valores de la Variable Aleatoria x (ventas de TV)
Probabilidad
Representación gráfica de la distribución de probabilidad
Distribuciones de
probabilidad discretas

10. Dr Jorge Ramírez Medina
EGADE Business School
Valor Esperado y Varianza
El valor esperado, o media, de una variable aleatoria
es una media de su localización.
La varianza resume la variabilidad en los valores de
la variable aleatoria.
La desviación estándar, , está definida como la
raíz cuadrada positiva de la varianza.
Var(x) =  2 = (x - )2f(x)
E(x) =  = xf(x)

11. Dr Jorge Ramírez Medina
EGADE Business School
Valor esperado
Número esperado de TVs
vendidas en un día.
x f(x) xf(x)
0 .40 .00
1 .25 .25
2 .20 .40
3 .05 .15
4 .10 .40
E(x) = 1.20
Valor Esperado y Varianza

12. Dr Jorge Ramírez Medina
EGADE Business School
Varianza y Desviación estándar
0
1
2
3
4
-1.2
-0.2
0.8
1.8
2.8
1.44
0.04
0.64
3.24
7.84
.40
.25
.20
.05
.10
.576
.010
.128
.162
.784
x -  (x - )2 f(x) (x - )2f(x)
Varianza de las ventas diarias =  2 = 1.660
x
TVs
al cuadrado
Desviación estándar de las ventas diarias = 1.2884 TVs
Valor esperado y varianza

13. Dr Jorge Ramírez Medina
EGADE Business School
Valor Esperado y Varianza
El valor esperado, o media, de una variable aleatoria
es una media de su localización.
La varianza resume la variabilidad en los valores de
la variable aleatoria.
La desviación estándar, , está definida como la
raíz cuadrada positiva de la varianza.
Var(x) =  2 = (x - )2f(x)
E(x) =  = xf(x)

14. Nos interesa el
contorno de la distribución
Dr Jorge Ramírez Medina
EGADE Business School

15. Asignación para
la siguiente sesión
Dr. Jorge Ramírez Medina
EGADE Business School

16. Fin Sesión Dos