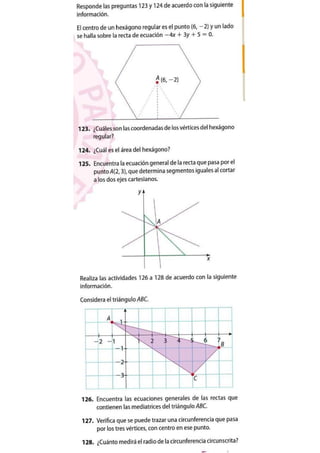
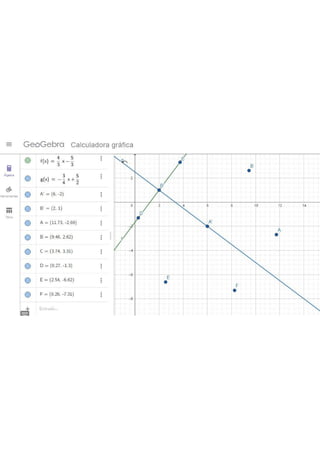
El documento proporciona información sobre un hexágono regular y un triángulo. El centro del hexágono está en (6, -2) y uno de sus lados está en la recta -4x + 3y + 5 = 0. Se pide calcular las coordenadas de los vértices y el área. En el triángulo ABC se dan las longitudes de sus lados y se pide encontrar las ecuaciones de las mediatrices y verificar si se puede trazar una circunferencia circunscrita que pase por sus vértices.

1. Responde las preguntas 123 y 124 de acuerdo con la siguiente
información.
El centro de un hexágono regular es el punto (6, —2) y un lado
se halla sobre la recta de ecuación —4x + 3y +5 =0.
$ (6,2)
123. ¿Cuáles son las coordenadas de los vértices del hexágono
regular?
124. ¿Cuál es el área del hexágono?
125. Encuentra la ecuación general de la recta que pasa por el
punto A(2, 3), que determina segmentos iguales al cortar
alos dos ejes cartesianos.
yA
e
il
Xx
Realiza las actividades 126 a 128 de acuerdo con la siguiente
información.
Considera el triángulo ABC.
| AE | Lab=d |
SS | Me
3 Y >S +
=2 —1 2 :
CPT TW la |
|
| —2+ | + =
1 | T t q TE ==
126. Encuentra las ecuaciones generales de las rectas que
contienen las mediatrices del triángulo ABC.
127. Verifica que se puede trazar una circunferencia que pasa
por los tres vértices, con centro en ese punto.
128. ¿Cuánto medirá el radio de la circunferencia circunscrita?

2. ETE TT -2+9 2 b => o SIE
? | ¡ | | | | Ne 1 ¡A OI... A O
i > _—b La ] =“ ed pe PP AAA +
y | *
A —
PP. .. - y
rabia Tes
403] LAR de, lo. de
Has INICLSS Pal EY los$ UNES, $
de L
in de SECOS | Vil lo:

3. Po
| ! . ¡TS rt
a
e A OO AN pe (Er0R]É— o
A
Pata callo ulLafotena: calsloros hands Y
E pc

4. AA Y) A _—_)
o
-p .
| |
e + elec NUM AE Y]
tes Mm ¿da ares. pues 0 obli 9
| |
| +
| |
AE Bo cost E Ay SoLeph
E 001
( ol
- | EA .| dz / cl Lb— —, A =. | $ , | |
Ex= LOs (M3 (HELLO Ey SES,
A TOA MIAN ci 77
i 1!
TON ER

5. GegvGebra Calculadora gráfica
lhoooo
.o.o..
.o
o
4 5
tx) = 373
80) = 4 x+>
A' = (6, -2)
B'=(2,1)
A = (11.73, -2.69)
B = (9.46, 2.62)
€ = (3.74, 3.31)
D = (0.27, -1.3)
E = (254, -6.62)
F = (8.26, -7.31)
Entrada...

6. 4
a ERA
¿ Í
] j
j 1 ;
4 f j Í J
a A: E —_—— or
i 1] ¡
i ;
1
]
|
—
a
Y
]
¡
a E TA A Y
E A A A AS A
PE A A A
Elan bo
=1(21+
¡ | j >
a
EAN
|
|
Í
A
ÓN
E
|
i
r
d

7. pa—*
a
Pal
Otros los pordimies de codo, lodo y
Las Colomo So pendiente AYO Oneigulay
1
r Palont tor No EC. de los 7
DAYS
Hedotrcer
y
MA EA
¡ao e e a E
E A A A o O

8. |
;
i
|
A
9
lÑ Ob+a
|
|
|
t
|
|
cul da:
7%
A
Es
e
e
EN
.. L
A ? E, e
AAA
228
Dr
]
A
Lodi
A
a
O o MUA EN a A A
Í
a
BOO A
|
1]
O AS

9. mu
GeaGebra Geometría
2 = Segmento [B, C]
O
El 28
E
genra
b = Segmento [C, Al :
$6. 0
arenias
— TE
<= Segmento [A, B] :
+ de
109 = 4-1 :
...
3
h(x) = 2 x—4
D = Intersección de LE :
O
O
| O .0= +?
O
O
O d = Circunferencia que pasa pór Cc

10. Phota Calesiamas
Ta disioncio dlconto:
de lay PUnaS MN pocas, Ese.
e