Este documento contiene 31 problemas de trigonometría y cálculo. Los problemas involucran calcular valores trigonométricos, áreas de figuras geométricas, simplificar expresiones y resolver ecuaciones trigonométricas. El documento proporciona gráficos, figuras y ecuaciones para ayudar a resolver cada problema.

1. MISCELANEA
1. Si: k =
g
20
26.rad
18


, además :
3k 

rad. =

ab
Calcular: E = ba 
a) 1 b) 2 c) 3
d) 5 e) 7
2. Calcular “x” (S : área)
a) 8
b) 9
c) 12
d) 15
e) 18
3. Del gráfico mostrado calcule tgx siendo: AB =
AC
a) 4/11
b) 2/11
c) 4/13
d) 11/4
e) 11/2
4. Siendo “x” e “y” ángulos agudos que
cumplen:
cos(2x + 10º) sec(6y - 10º) = 1
sen(x + 2y) = cos(3x + y – 20º)
Calcule: sen(2x + 2y)
a) 3/5 b) 2 /2 c) 3 /2
d) 4/5 e) ½
5. De la figura, O es centro AC = a; BC = b.
Hallar: Tg  en función de a  b
A O D
C
B
A)
a b
a b


B)
a
b
C)
a b
a b


D)
b
a
E)
a b
a b


6. Desde lo alto de un faro se divisa un objeto
en Tierra con un ángulo de depresión “” 30
m más atrás, se encuentra otro objeto el
cual es observado con un ángulo de
depresión de 45º.
Si: tg = 3. Calcular la altura del faro.
a) 10 m b) 30 c) 45
d) 50 e) 55
7. Del gráfico calcular: “tg ”
a) -1/5
b) -2/5
c) -3/5
d) -4/5
e) -1
8. Hallar el valor positivo de “” menor a una
vuelta tal que:
tg
7
2
+ tg
7
3
+ tg
7
4
= cos  . tg
7
5
a) 90º b) 120º c) 150º
d) 180º e) 270º
9. Calcular:
E = 1senxx2cos54 
a) 1 b) 2 c) 3
d) 2 e) 3
10. Del gráfico calcular el área del triángulo
sombreado:
a)
2
1cossen 
d)
2
cossen1 
b)
2
cossen1 
e)
2
cossen 
c)
2
cossen1 
X6S 3S
A D
EA
C
x
37º
-
1
8
x

x
y


2. 11. Del gráfico mostrado; hallar “x”:
a) 4 3
b) 4 6
c) 3 6
d) 8 6
e) 6 3
12. Simplificar:
)CtgxCosx()TgxSenx(
)CosxSenx1(
N
2



A) 1 B) 2 C) –1
D) Tgx E) Ctgx
13. En la figura elárea sombreada es equivalente
a:
y
x
x + y = 12 2
A) Sen (1 - Cos) B) -Sen (1 - Cos)
C) -Cos (1 - Sen) D) Cos (1 - Sen)
E) Sen Cos
14. 2. Sabiendo que:
2Tg 1
Tg 1
4
32

  
  
 
Sen 0  . Hallar: R 13Sen 5Ctg  
a) 3 b) 9 c) 5
d) 11 e) 7
15. Simplificar la siguientes expresión:
M = Sen2
(x +y) – 2Sen (x +y) Cosx Seny +Sen2
y
A) Sen2
x B) Cos2
y C) 1
D) Cos2
x E) Sen2
y
16. Calcule el valor de:
  1 Tg32º 1 Tg13º 
a) 1 b) 2 c) 3
d) 4 e) 5
17. Hallar el valor de: A = Tan20º + Tan40º +
3 Cot70º Cot50º
A) 3 B) 1 C) - 2
D) 2 E) - 3
18. Los catetos de un triángulo miden 1 + Cos50º
+ Sen50º y 1 – Cos50º + Sen50º determine la
medida del menor ángulo de dicho triángulo
A) 55º B) 65º C) 45º
D) 35º E) 25º
19. Simplificar:
Cotx
2
x
Tan
2
1
2
x
Tan
2
1
Cscx
K



A) 1 B) 2 C) 1/2
D) –1 E) -2
20. Si: x 
6
π5
,
4
π
.
Calcular el máximo valor de:
E = Sen2
x Cot
2
1
2
x
 Sen2x
A) 2/3 B) 1 C) –1
D) 3/2 E) 2/5
21. Simplificar: 











 θCsc
θCsc
1
θSec
θSec
1
2R
A) Sen2 B) Cos2 C) Tan2
D) 2Sen2 E) 2Cos2
22. Del gráfico mostrado, calcular: SenCos,
sabiendo que: AC = 2BD
4
2
A B
C D
A) 1/4 B) 1/8 C) 1/6
23. Factorizar:
A = Cos + Cos3 + Cos5 + Cos7


x
2
6
4

3. Y
X
Y = ASenCx
( c > 0 )
-3
3
42
M N
3
2
A
C2
)e
C
A2
)d
A
C
)c
C
A
)b
C
A
)a









A) 1/2Sen8 Csc B) Sen8Csc
C) 1/4Sen8Cos D) 1/8Sen
E) Sen8Cos
24. El equivalente de :
x9Cosx7Cosx5Cosx3Cos
x9Senx7Senx5Senx3Sen


es Tgax, hallar “a”
A) 3 B) 4 C) 5
D) 6 E) 7
25. Calcular: U =Cosx +Cos(120º - x) +Cos(120º
+ x)
A) 0 B) 1 C) –1
D) –1/2 E) 1/2
26. Calcular: H = Cos2
x + Cos2
x (120º - x) + Cos2
(120º + x)
A) 1/2 B) 1 C) 3/2
D) 0 E) ¾
29. Determinar el Área de la región sombreada.
30. En cuántos puntos la función Y = Senx corta
a la gráfica de Y = Cosx en ] 0 ; 11[
a) 9 b) 10 c) 12
d) 11 e) 13
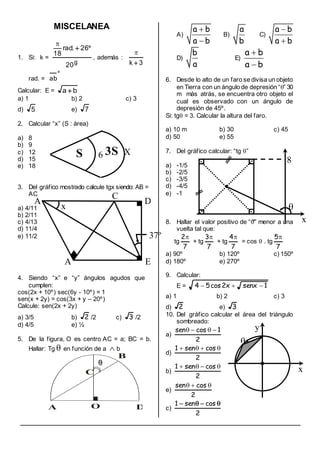
31. Indicar la suma de las ordenadas de los
puntos M y N en la gráfica adjunta:
a) 23 b) 23
c) 2 d) - 2
e)
2
23