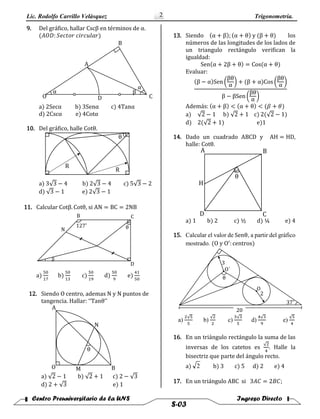
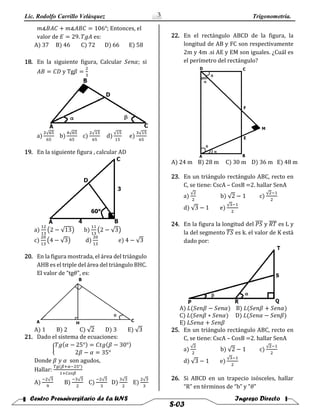
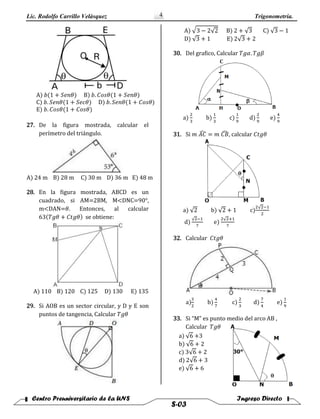
1. El documento presenta 33 problemas de trigonometría que involucran cálculos de funciones trigonométricas como seno, coseno, tangente, cotangente y cosecante para ángulos en triángulos rectángulos y no rectángulos. Los problemas deben resolverse calculando las funciones trigonométricas dadas la información proporcionada en cada gráfico o expresión.

1. Centro Preuniversitario de la UNS Ingreso Directo
S-03
b
a
H
COSenA 
b
c
H
CA
CosA 
c
a
CA
COTanA 
a
b
CO
HCscA 
c
b
CA
HSecA 
a
c
CO
CA
CotA 
UNIVERSIDAD NACIONAL DEL SANTA
CEPUNS
Ciclo 2016 – I
TRIGONOMETRÍA
“Razones Trigonométricas”
PROBLEMAS PROPUESTOS
1. En un triángulo rectángulo ABC, recto en
B, se cumple que:
(SenA)CosC
+ (CosC)SenA
=
2√9
3
3
Entonces el valor de:
E = TanC + CotC es:
a) 9/4 b) 9√2/4 c) 9√3/4
d) 4√3/9 e) 4√2/9
2. En la figura, el triángulo ABC es
rectángulo, recto en A, CP=2 cm., PB=3
cm. Halle Tanα.
30˚ α
A B
C
P
a)
√3
9
b)
5√3
9
c)
2
9
√3 d)
√3
3
e)
2√3
3
3. En un triángulo ABC (recto en B) se
cumple que TanA =
5
12
y su perímetro es
90. Calcular el cateto mayor.
a) 36 b) 20 c) 15 d) 48 e) 24
4. Del gráfico, calcule Cotα +
√3
3
si AC̅̅̅̅ = 2AB̅̅̅̅.
α
60˚
A
B
C
a) 1 b) 2 c)
1
3
d) 3 e)
1
2
5. Del gráfico, calcule 7Tanθ + 2√3.
7
4
4
θ
√21
a) 4 b) 2 c) 1 d) 5 e) 3
6. Del gráfico, calcule 17Tanθ.
37˚
53˚
θ
a) 5 b) 3 c) 2 d) 4 e)6
7. Si α y θ son ángulos agudos y
complementarios, tales que:
Senα =
3
2x + 3
y Secθ =
4x + 1
2
Halle el valor de: Senθ + Cosα −
2
5
a)
6
5
b)
8
5
c)
3
5
d)
4
5
e)
1
5
8. Del gráfico , hallar TanαTanβ
2 3
β
α
a)
1
2
b)
3
2
c)
2
3
d)
3
5
e)
5
3
Semana Nº 3

2. Lic. Rodolfo Carrillo Velàsquez Trigonometría.
Centro Preuniversitario de la UNS Ingreso Directo
S-03
2
9. Del gráfico, hallar Cscβ en términos de α.
(𝐴𝑂𝐷: 𝑆𝑒𝑐𝑡𝑜𝑟 𝑐𝑖𝑟𝑐𝑢𝑙𝑎𝑟)
A
O
B
CD
α
βα
a) 2Secα b) 3Senα c) 4Tanα
d) 2Cscα e) 4Cotα
10. Del gráfico, halle Cotθ.
R
R
θ
a) 3√3 − 4 b) 2√3 − 4 c) 5√3 − 2
d) √3 − 1 e) 2√3 − 1
11. Calcular Cotβ. Cotθ, si AN = BC = 2NB
127˚
β
θN
B C
D
a)
50
17
b)
50
13
c)
50
19
d)
50
9
e)
41
50
12. Siendo O centro, ademas N y N puntos de
tangencia. Hallar: ‘‘Tanθ’’
θ
MO B
N
A
a) √2 − 1 b) √2 + 1 c) 2 − √3
d) 2 + √3 e) 1
13. Siendo (α + β); (α + θ) y (β + θ) los
números de las longitudes de los lados de
un triangulo rectángulo verifican la
igualdad:
Sen(α + 2β + θ) = Cos(α + θ)
Evaluar:
(β − α)Sen (
βθ
α
) + (β + α)Cos (
βθ
α
)
β − βSen (
βθ
α
)
Además: (α + β) < (α + θ) < (𝛽 + 𝜃)
a) √2 − 1 b) √2 + 1 c) 2(√2 − 1)
d) 2(√2 + 1) e)1
14. Dado un cuadrado ABCD y AH = HD,
halle: Cotθ.
θ
H
D C
BA
a) 1 b) 2 c) ½ d) ¼ e) 4
15. Calcular el valor de Senθ, a partir del gráfico
mostrado. (O y O′:centros)
3
2
37˚
O´
O
θ
20
a)
2√5
5
b)
√2
2
c)
3√3
5
d)
4√3
9
e)
√5
4
16. En un triángulo rectángulo la suma de las
inversas de los catetos es
√2
4
. Halle la
bisectriz que parte del ángulo recto.
a) 2 b) 3 c) 5 d) 2 e) 4
17. En un triángulo ABC si 3𝐴𝐶 = 2𝐵𝐶;

3. Lic. Rodolfo Carrillo Velàsquez Trigonometría.
Centro Preuniversitario de la UNS Ingreso Directo
S-03
3
𝑚∡𝐵𝐴𝐶 + 𝑚∡𝐴𝐵𝐶 = 106°; Entonces, el
valor de 𝐸 = 29. 𝑇𝑔𝐴 es:
A) 37 B) 46 C) 72 D) 66 E) 58
18. En la siguiente figura, Calcular 𝑆𝑒𝑛𝛼; si
𝐴𝐵 = 𝐶𝐷 y Tg𝛽 =
2
3
a)
2√65
65
b)
4√65
65
c)
2√15
65
d)
√15
15
e)
3√15
65
19. En la siguiente figura , calcular AD
a)
12
13
(2 − √13) b)
11
13
(2 − √3)
c)
20
13
(4 − √3) d)
20
13
e) 4 − √3
20. En la figura mostrada, el área del triángulo
AHB es el triple del área del triángulo BHC.
El valor de “tg𝜃”, es:
A) 1 B) 2 C) √2 D) 3 E) √3
21. Dado el sistema de ecuaciones:
{
𝑇𝑔(𝛼 − 25°) = 𝐶𝑡𝑔(𝛽 − 30°)
2𝛽 − 𝛼 = 35°
Donde 𝛽 𝑦 𝛼 son agudos,
Hallar:
𝑇𝑔(𝛽+𝛼−25°)
1+𝐶𝑜𝑠𝛽
A)
−2√3
9
B)
−3√3
2
C)
−2√3
3
D)
3√3
2
E)
2√3
3
22. En el rectángulo ABCD de la figura, la
longitud de AB y FC son respectivamente
2m y 4m .si AE y EM son iguales. ¿Cuál es
el perímetro del rectángulo?
A) 24 m B) 28 m C) 30 m D) 36 m E) 48 m
23. En un triángulo rectángulo ABC, recto en
C, se tiene: CscA – CosB =2. hallar SenA
a)
√2
2
b) √2 − 1 c)
√2−1
2
d) √3 − 1 e)
√3−1
2
24. En la figura la longitud del 𝑃𝑆̅̅̅̅ y 𝑅𝑇̅̅̅̅ es L y
la del segmento 𝑇𝑆̅̅̅̅ es k. el valor de K está
dado por:
A) 𝐿(𝑆𝑒𝑛𝛽 − 𝑆𝑒𝑛𝛼) B) 𝐿(𝑆𝑒𝑛𝛽 + 𝑆𝑒𝑛𝛼)
C) 𝐿(𝑆𝑒𝑛𝛽 ∗ 𝑆𝑒𝑛𝛼) D) 𝐿(𝑆𝑒𝑛𝛼 − 𝑆𝑒𝑛𝛽)
E) 𝐿𝑆𝑒𝑛𝛼 + 𝑆𝑒𝑛𝛽
25. En un triángulo rectángulo ABC, recto en
C, se tiene: CscA – CosB =2. hallar SenA
a)
√2
2
b) √2 − 1 c)
√2−1
2
d) √3 − 1 e)
√3−1
2
26. Si ABCD en un trapecio isósceles, hallar
“R” en términos de “b” y "𝜃"

4. Lic. Rodolfo Carrillo Velàsquez Trigonometría.
Centro Preuniversitario de la UNS Ingreso Directo
S-03
4
A) 𝑏(1 + 𝑆𝑒𝑛𝜃) B) 𝑏. 𝐶𝑜𝑠𝜃(1 + 𝑆𝑒𝑛𝜃)
C) 𝑏. 𝑆𝑒𝑛𝜃(1 + 𝑆𝑒𝑐𝜃) D) 𝑏. 𝑆𝑒𝑛𝜃(1 + 𝐶𝑜𝑠𝜃)
E) 𝑏. 𝐶𝑜𝑠𝜃(1 + 𝐶𝑜𝑠𝜃)
27. De la figura mostrada, calcular el
perímetro del triángulo.
A) 24 m B) 28 m C) 30 m D) 36 m E) 48 m
28. En la figura mostrada, ABCD es un
cuadrado, si AM=2BM, M<DNC=90°,
m<DAN=𝜃. Entonces, al calcular
63(𝑇𝑔𝜃 + 𝐶𝑡𝑔𝜃) se obtiene:
A) 110 B) 120 C) 125 D) 130 E) 135
29. Si AOB es un sector circular, y D y E son
puntos de tangencia, Calcular 𝑇𝑔𝜃
A) √3 − 2√2 B) 2 + √3 C) √3 − 1
D) √3 + 1 E) 2√3 + 2
30. Del grafico, Calcular 𝑇𝑔𝛼. 𝑇𝑔𝛽
a)
2
3
b)
1
3
c)
1
9
d)
2
9
e)
4
9
31. Si 𝑚 𝐴𝐶̂ = 𝑚 𝐶𝐵̂ , calcular 𝐶𝑡𝑔𝜃
a) √2 b) √2 + 1 c)
2√2−1
2
d)
√2−1
7
e)
2√2+1
7
32. Calcular 𝐶𝑡𝑔𝜃
a)
3
2
b)
4
7
c)
2
3
d)
7
4
e)
1
9
33. Si “M” es punto medio del arco AB ,
Calcular 𝑇𝑔𝜃
a) √6 +3
b) √6 + 2
c) 3√6 + 2
d) 2√6 + 3
e) √6 + 6