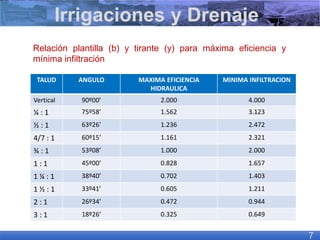
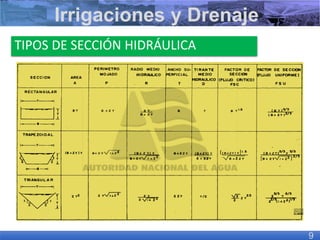
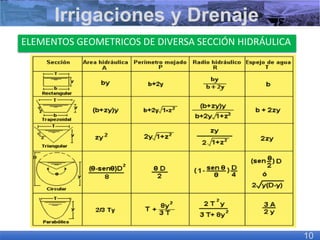
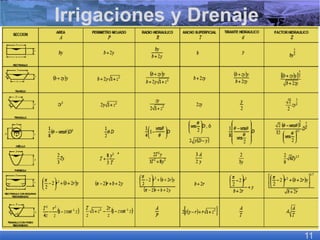
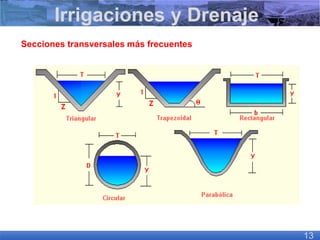
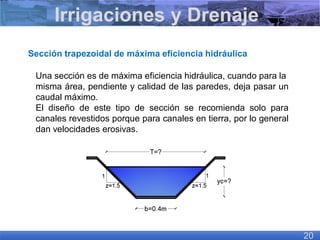
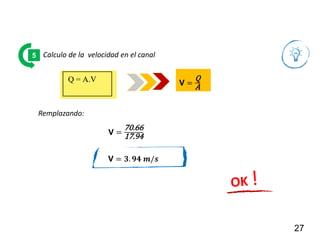
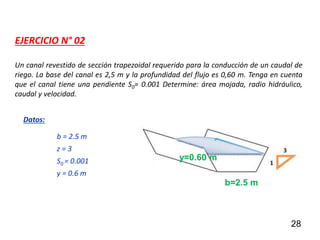
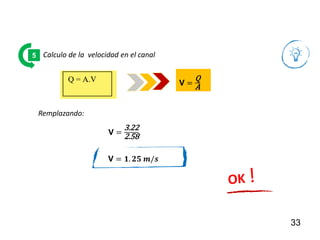
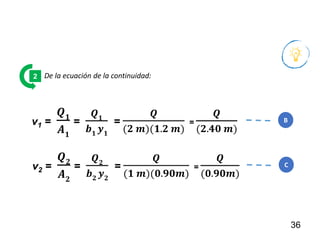
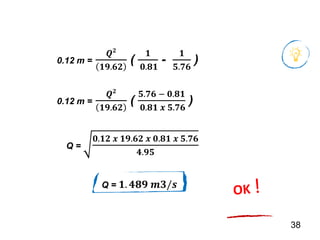
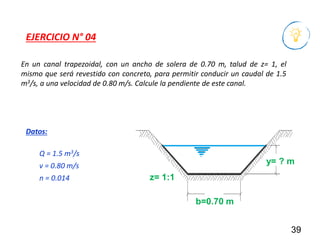
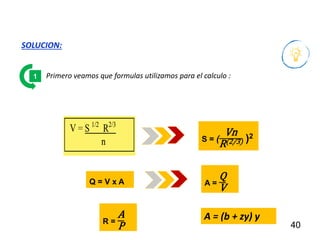
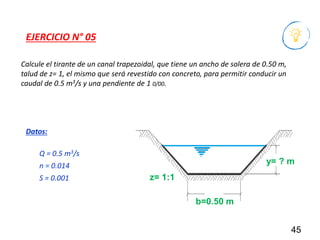
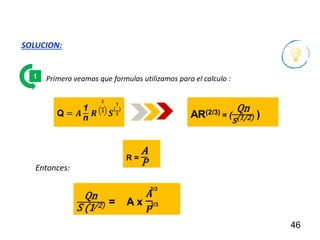
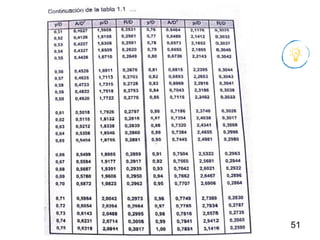
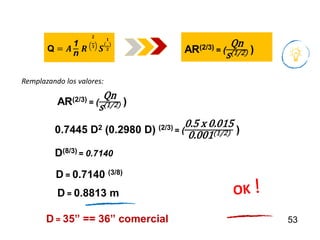
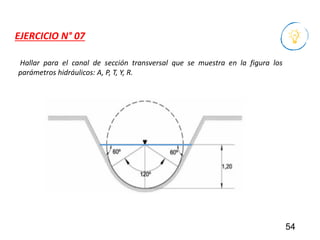
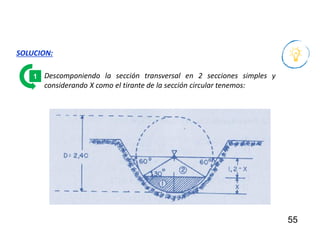
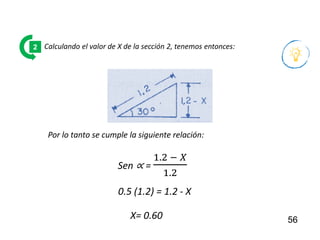
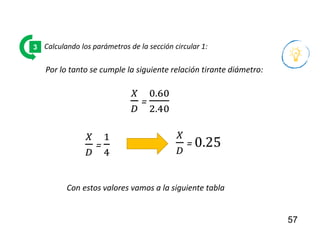
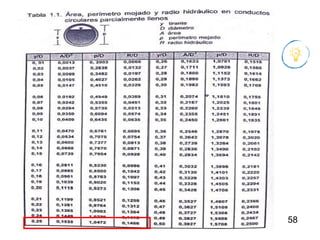
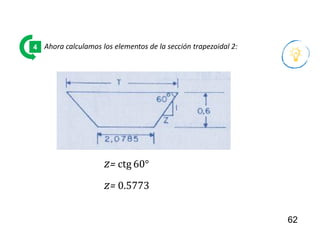
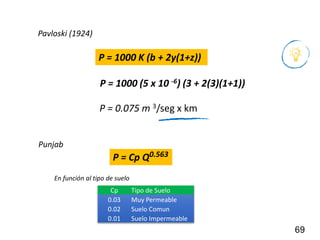
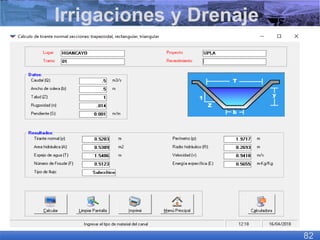
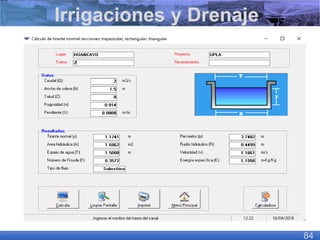
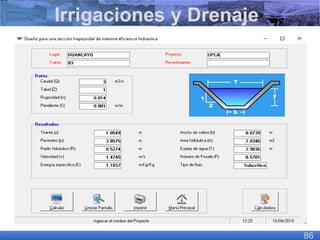
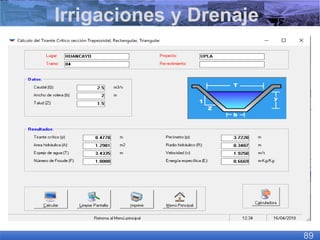
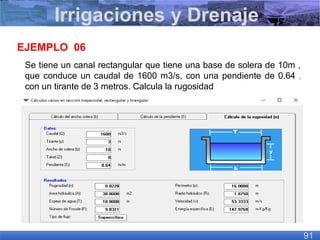
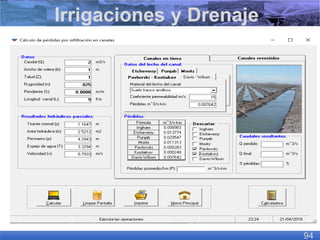
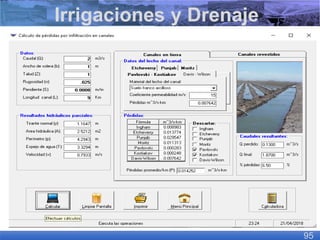
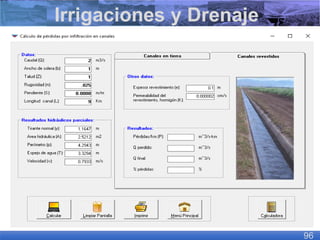
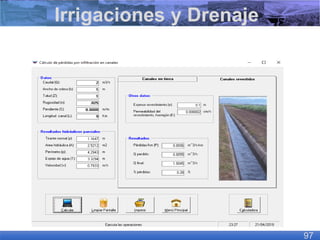
El documento presenta criterios y condiciones para el diseño de estructuras de conducción de agua, enfocándose en el cálculo hidráulico utilizando la fórmula de Manning. Se discuten secciones de máxima eficiencia hidráulica y mínima infiltración, así como la importancia del número de Froude en el análisis del flujo. También se incluyen ejemplos prácticos de cálculos de caudal y velocidad en canales de distintas geometrías.