Este documento presenta la primera unidad de álgebra de una alumna. Incluye definiciones de conceptos algebraicos como álgebra, exponentes, suma y resta algebraica. También contiene ejemplos resueltos de operaciones como suma, resta, división y productos notables. Finalmente, presenta el triángulo de Pascal y ejercicios resueltos de factorización.

1. CEDART
DAVID ALFARO SIQUEIROS
BACHILLERATO DE ARTE Y HUMANIDADES
INBA Y BELLAS ARTES
ÁLGEBRA
MAESTRO: ING. VICTOR MANUEL MORALES ÁRZAGA
ALUMNA: LUISA EDITH CEPEDA GLEZ
GRADO: _____1________
GRUPO: _____1________
FECHA DE ENTREGA: jueves 16--12--2010

2. Índice
Primer parcial……………………………………………………………. 2
Segundo parcial…………………………………………………………….5
Tercer parcial………………………………………………………………10

3. INTRODUCCIÓN
A) DEFINIR LOS SIGUIENTES CONCEPTOS:
ÁLGEBRA
Para los usos matemáticos de la palabra álgebra como estructura algebraica, véase
álgebra no asociativa, álgebra asociativa, álgebra sobre un cuerpo. El álgebra es la rama
de las matemáticas que estudia las estructuras, las relaciones y las cantidades (en el caso
del álgebra elemental). Junto a la geometría, el análisis matemático, la combinatoria y la
teoría de números. La palabra «álgebra» es de origen árabe, deriva del tratado escrito
por el matemático persa Muhammad ibn Musa al-Jwarizmi, titulado Kitab al-yabr wa-l-
muqabala (en árabe ‫( )ل ةك تاب ال ج بر وال م قاب‬que significa "Compendio de cálculo por el
método de completado y balanceado"), el cual proporcionaba operaciones simbólicas
para la solución sistemática de ecuaciones lineales y cuadráticas. Etimológicamente, la
palabra «álgebra» ‫( ربج‬yabr) , proviene del árabe y significa "reducción".
APLICACIONES
ASIDUIDAD CON QUE SE ESTUDIA// ADORNO SOBREPUESTO EN UN MATERIAL
DIFERENTE.
TÉRMINOS ALGEBRAICOS
MEDIA ARITMÉTICA, PROMEDIO.
EXPONENTES
Número que, puesto arriba a la derecha de otro llamado base, indica las veces en que
hay que multiplicarse por si mismo.
B) EJEMPLO DE SUMA ALGEBRAICA (PERÍMETRO)
SI SUMAMOS EL SALÓN DE 1´´1´´ Y EL DE 1´´A´´ NOS DA UN TOTAL DE
900 MTS. ¿Cuánto MIDE C/U? R: 450
X+X=900
X+X=900 X=450
2X=900 1´´ 1´´
X=900÷2 1´´ A´´
Marisol tiene tres repisas llenas de juguetes. Su hermana Juana quiere saber cuantos juguetes
deben de ir en cada repisa… ¿Cuántos debe haber en cada repisa, si son un total de 60
muñecos?
3X=60
3X=60
X=60÷3 = 20
X=20

4. 2- RESOLVER¨:
(5A² – 2 a³ +a ) + (4 a + 3 a²) + (5 a³ – 2 a +7)
8a² +3a³+3a+7 acomodación 3a ³+ 8a² +3a+7 polinomio cubico
(3/4x ² - 4/3x +2)+ (1/6x – 5/2 x²+ 7/8)
x² - ¾ - 5/2= -- 14/8 x²
x - 4/3 - 1/6 = -- 21/18x
#- 2+7/8= 23/8
-- 14/8 x² -- 21/18x +23/8 trinomio cuadrado
(4y- 5z+3)+ (4z-y+2)- (3y -2z-1)
6y—3z+4 trinomio lineal
(1/2 m + 3/5 m – 4/7) + (3/8 m- 5/4) + (5/3 m – 3/10 m)
M² ½- 3/10 =4/20 M²
M 3/5+ 3/8=39/40 M + 5/3 m=317/120 M
# -4/7- 5/4= - 51 / 28
4/20 M² + 317/120 M - 51 / 28 TRINOMIO CUADRADO
(2pq – 3p² + 4pq²)+ (Pq-5pq² -7p ² q)+(- 4pq² +3pq – p ² q)
6P Q – 3P ² – 5PQ ² – 8P ² Q
–8P ² Q– 5PQ ² – 3P ² + 6P Q POLINOMIO CUBICO
CONTINUACION
RESTA
A) EJEMPLIFICA UNA APLICACIÓN DE LA RESTA ALGEBRAICA (DESCRIBE EL
PROBLEMA AGREGA IMAGEN O ESQUEMA Y RESUELVE)
B) MIRNA TIENE CINCO ROSAS Y TRES TULIPANES EN SU JARDIN. AYER BRENDA
LE QUITO DOS ROSAS, PERO LE DIO UN TULIPAN.
NATASHA LE QUITO TRES TULIPANES PERO LE DIO UNA ROSA. ¿Cuántas
ROSAS Y TULIPANES LE QUEDARON?
(5N+3M) – (2N+1M) - (3M+N)
-2N - 1M BINOMIO LINEAL
RESUELVE LAS SIGUIENTES OPERACIONES
(5M+4N–7) – (8N –7) + (4M–3N+5) – (- 6M+4N–3)
15M- 11N+ 15 TRINOMIO LINEAL
(4M4 – 3M³+ 6M² +5M- 4) – (6M³- 8M² -3M – 1)
4M4- 9M³+14 M²+8M – 5 POLINOMIO CUARTO GRADO
(- XY4- 7Y³+XY²) + (- 2 XY4+5Y – 2) – (- 6Y³ +XY² +5)
- 3 XY4 - 1 Y³ +0XY² +5Y – 7 POLINOMIO CUARTO GRADO
(1/6X+ 3 /8 Y - 5) - (8 / 3Y - 5 / 4) + (3/2 X + 2 /9)
20/12X - 15/24Y - 127/36 TRINOMIO LINEAL
DISEÑAR OTRA RESTA CON FRACCIONES (MINIMO TRINOMIO)
(1/2X² - 3/10 X +1/6) – (3/8+5/10 X²) + (3/6 X)
-5/20X² +12/60X -10/48 TRINOMIO CUADRADO

5. INTRODUCCIÓN
B) DEFINIR LOS SIGUIENTES CONCEPTOS:
¿Qué es división algebraica?
División de expresiones algebraicas. Una expresión algebraica es aquella en la que se
utilizan letras, números y signos de operaciones.
Es la operación que tiene como objeto, dado el producto de dos factores (dividendo) y
uno de los factores (divisor) hallar el otro factor.
Definición
Son aquellos productos que se rigen por reglas fijas y cuyo resultado puede hallarse por
simple inspección. Su denominados también "Identidades Algebraicas". Son aquellos
productos cuyo desarrollo es clásico y por esto se le reconoce fácilmente. Es una
multiplicación inversa. Está compuesta por dividendo, divisor, cociente y
residuo.
Propiedades de la división algebraica
División: es una multiplicación inversa. Está compuesta por dividendo, divisor,
cociente y
Residuo.
PROPIEDADES DE LA DIVISION:
P.Reintegrativa.
En una división dada si el cociente se multiplica por el divisor da como producto el
dividendo.
P. Divisor 1
En cualquier división el divisor es 1 el dividendo y el cociente son iguales.
Existen tres tipos de división algebraica:
(Solo se mencionan dos)
* Monomio entre monomio
* Polinomio entre monomio

6. Reglas
- los coeficientes se dividen o simplifican aplicando la ley de los signos.
- los exponentes se restan indicando el resultado donde estaba el mayor.
- {El primero solo se indica si es el único resultado}
-
[NOTA:
EL NUMERO DE TERMINOS ES EL NUMERO DE RESULTADOS]
¿Cuáles son los elementos (partes) de la división?
Sus elementos son:
* Dividendo
*Divisor
*Cociente
Residuo
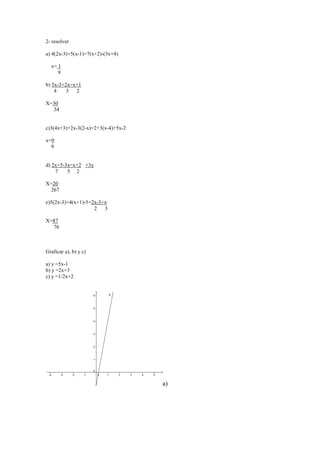
RESOLVER:
8m9n2-10m7n4-20m5n6+12m3n8% 2m2n3= 4m7-5m5n-10m3n+6mn5
2mn 2 2 2
20x4-5x3-10x2+15x% 5x= 4x3-1x2-2x+3
5 5
4a8-10a6-5a4% 2a3= 2a5-5a3-2a
2 2ª2
2x2y+6xy2-8xy+10x2y2% 2a3= x+3y-4+5xy
2y 2x 2xy 2
3x2 +2x-8% x+2= 3x+8
2x3-4x-2% 2x+2= x2+3x2
2a4-a3+7a-3% 2a+3= a3-1
14y2-71y-33% 7y+35= 2y
Si un espacio rectangular tiene el área de 6x2-19x+15 y la anchura es de 3x-5
¿Cuánto mide la base?

7. 2x-3
6- expresar conclusiones personales sobre la primera unidad ¨´operaciones algebraicas¨´
Es la generalización de las ideas de la aritmética, la rama de la matemática en la que las
cantidades desconocidas se pueden representar por letras y así determinar sus valores
para resolver problemas.
Productos Notables
¿Que son los productos notables?
Productos notables
Ciertos productos que cumplen reglas fijas y cuyo resultado puede ser escrito por
simple inspección
Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones
algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la
multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la
resolución de muchas multiplicaciones habituales.
Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la
factorización de una diferencia de cuadrados perfectos es un producto de dos binomios
conjugados y recíprocamente.
Es la multiplicación de ciertas expresiones utilizando reglas para obtener el resultado.
a) Binomios a una potencia= EXPRESIONES
IGUALES QUE SE MULTIPLICAN VARIAS
VECES ENTRE SI.
b) Binomio con Termino Común:
Cuadrado del común
Suma o resta de los no comunes por el común
Producto de los no comunes
c) Binomios Conjugados:
Cuadrado del primero
(-) menos cuadrado del segundo
I- BINOMIO AL CUADRADO
II- BINOMIO AL CUBO
III- BINOMIOS A UNA POTENCIA SUPERIOR
IV- BINOMIO AL CUADRADO:
Cuadrado del primero
Doble producto del primero por el segundo

8. Cuadrado del segundo
V- BINOMIO AL CUBO
Cubo del primero
Triple producto del cuadrado del primero por el segundo
Cubo del segundo
VI- BINOMIOS A UNA POTENCIA SUPERIOR
Te guías por el triangulo de pascal según la potencia
Se va a ir repitiendo el problema cuantas veces sean necesarias
Se multiplica el numero afuera del paréntesis por el de adentro
En la calculadora se oprime el botón
Exponente por el siguiente numero del otro paréntesis exponente
Triangulo de pascal
Triangulo de pascal
El triángulo de Pascal en matemáticas es un conjunto infinito de números enteros
ordenados en forma de triángulo que expresan coeficientes binomiales. El interés del
Triángulo de Pascal radica en su aplicación en álgebra y permite calcular de forma
sencilla números combinatorios lo que sirve para aplicar el binomio de Newton.
También es conocido como Triángulo de Tartaglia. En países orientales como China,
India o Persia, este triángulo se conocía y fue estudiado por matemáticos como Al-
Karaji, cinco siglos antes de que Pascal expusiera sus aplicaciones, o por el astrónomo y
poeta persa Omar Jayyam (1048-1123). En China es conocido como Triángulo de
Yanghui, en honor al matemático Yang Hui, quien lo describió el año 1303.1

9. Ejercicio:
(3a+4)2= 9ª2+24ª+16
(2x2-5)2= 4x4-20x2+25
(7m+8n)2=49m2+112mn+64n2
(4ª+5)3= 64ª3+240ª+125
(2ª3-7)3=8ª9-84ª6+294ª3-343
(5m+4)3=125m3+300m2+240m+64
(3x+2)4=1(3x)4(2) °4(3x)3(2)1 6(3x)2(2)2 4(3x)1(2)31(3x)0(2)4
81x4+216x3+216x2+96x1+16
(2x2-4)5=32x5-320x4+1,280x3-2560x2+2560x-32
(4y3+3)6=4,096x6+18,432x5+34,560x4+34,560x3+19,440x2+5,832x+729
(2x+3) (2x+5)=4x2+16x+15
(x2-1) (x2+1)=x4-1x2-1
(m+4) (m-2)=m2-2m-8
(3ª-7) (3ª+7)=9ª2-49
(5ª+36)(5ª-26)=25ª2+50ª-936
(4x3+3)(4x3-3)=16x6-9
(a2-1)(a2-4)=a4-3ª2-4

10. Factorización
Define qué es factorización.
En álgebra, la factorización es expresar un objeto o número (por ejemplo, un
número compuesto, una matriz o un polinomio) como producto de otros objetos
más pequeños (factores), (en el caso de números debemos utilizar los números
primos) que, al multiplicarlos todos, resulta el objeto original.
Ilustra en un mapa conceptual los diversos métodos de factorización
Factoriza las sig. Expresiones.
a) 25a 2 – 64b2 =(5ª+8)(5ª-8)
b) 8m2 – 14m- 15=(-1m+1)(2m-5)
c) X2 – 15x+54=(x-6)(x-9)
d) 5x2 -13x +6=(x+x)(1+6)
e) 27ª9 –b3=(7ª3 +b)(7ª3-b)
f) 5a 2+10ª=5ª(1ª+2)
g) N2 -14n +49=(n-7)2
h) X2 -20x -300=(x -2)(x +150)
i) 9x6 -1=(3x3-1) (3x3+1)
j) 64x3 +125=(8x+5)(8x2-40x+25)
k) X2 -144=(x+72)(x-72)
l) 2x2+11x+12= 2(x+6)
m) 4x2y – 12xy2=xy(4x-12y)
n) Xw – yw + xz – yz=(w+z)(x-y)
o) X2 +14x + 45=(x+5)(x+9)
p) 6y2 – y – 2=(2y+2)(3-2)
q) 4m2 – 49=(2m+7)(2m-7)
r) X2 – x – 42=x(x-4x)
s) 2m2 + 3m – 35=(2m+5)(2m-7)
t) A2 – 24ª + 119=(a+12)2
Investiga la aplicación de la factorización en la solución de ecuaciones cuadráticas.
Solución de la ecuación de segundo grado por medio de la factorización
El método para solucionar ecuaciones de segundo grado por medio de la factorización es un poco
complicado pero con algo de práctica se puede obtener cierta habilidad, este método se basa en que el
producto de dos o más factores es cero, si cualquiera de los factores es cero.
De este modo la ecuación (X-4)(X-3) = 0 se satisface ya sea para X = 4 o para X= 3
Nota: Una buena habilidad adquirida en este método nos pueda dar buenos frutos en la solución de no
solo ecuaciones de segundo grado si no incluso de grado superior.
Los pasos a seguir son los siguientes:
Coloca todos los miembros del lado izquierdo de la ecuación e iguálalos a cero Factoriza el miembro de la
izquierda en factores de primer grado. Cada factor así formado de primer grado se iguala a cero y se
obtienen así las raíces.

11. Nota: Si no se cumple el primer paso entonces la ecuación no es factorizable.
Ahora bien te has de preguntar querido lector como se hace en la practica, pues aquí esta la solución con
el siguiente ejemplo
X^2 = 2X + 3
X^2 - 2X - 3 = 0 (Paso 1)
Para el caso dos el secreto esta en encontrar dos números que sumados nos den -2 y al multiplicarlos
nos den como resultado - 3.
Esos números son -3 y 1 a continuación dichos números los sustituimos por -2 y la ecuación nos da como
resultado:
X^2 - 3X + X -3 = 0
X(X - 3) + (X -3) = 0
(X + 1)(X - 3)=0 (Paso 2)
Solución a la ecuación
X = -1
X=3 (Paso 3)
No obstante, no siempre es fácil encontrar ambos números sobre todo si son cantidades grandes, ahora
bien, un problema muy común es que en el primer término de la ecuación el coeficiente sea mayor a uno
(A > 1) y es aquí donde tenemos una solución muy interesante para poder factorizar los términos.
Resulta que debemos multiplicar el coeficiente de X2 por el tercer término ( C ), lo que nos dará como
resultado un número más grande.
Una vez que hemos hecho el paso anterior la tarea se centra en encontrar dos números que sumados nos
el segundo termino y multiplicados nos den el numero grande encontrado.
Es así como funciona:
2X^2 - X -6 = 0
(2)(-6) = -12 (Obtenemos el numero)
Los dos números son 3 y -4 los cuales sumados nos dan - 1 y multiplicados nos dan -12 que es el gran
numero obtenido.
2X^2 - 4X + 3X -6 = 0 (Sustitución de los dos números)
2X(X - 2) + 3(X - 2) (Factorización por factor común)
(X - 2)(2X + 3) = 0 (Ecuaciones de primer grado)
X=2 (Resolución de las ecuaciones de primer grado)
X = -3/2

12. Conclusiones personales sobre la unidad de factorización.
Es una herramienta útil para separar los sub-conjuntos de los conjuntos simplificando así la reagrupación
FRACCIONES ALGEBRAICAS
Realiza las operaciones con fracciones algebraicas:
X2 – 16 = x-4
X2 + 8x + 16 x+4
4x2 – 20x = 4
X2 – 4x -5 x+1
3ª – 9b = 3
6ª – 18b 6
X2 – 6x + 9 * x2 + 6x + 5 = (x+3)(x+5)(x+1)
X2 – 7x + 12 3x2 + 2x – 1 (x+4)3(x-3)
7x + 21 * x2 – 5xy + 4y2 = 7(x+5)(x-1)
X2 – 16y2 4x2 + 11x (x+4y)(x-4y) 4
X2 – 3x – 10 * 2x + 10 =2
X2 – 25 6x + 12 6
X – 4 * 4x + 8 = 4(x+2)
2x + 8 x2 – 16 2(x+4)2
3x – 15 ÷ 12x + 18 =3x-1512+3x+9 12x+1812x2+36
X+3 4x + 12 X+3 4x + 12
4x2 – 9 ÷ 2x – 3 = 4(x-2)2x-3
X + 3y 2x + 6y x+3y 2(x+3)
X2 – 14x - 15 ÷ x2 – 12x – 45 = (x-7)(x+2)
X2 – 4x – 45 x2 – 6x – 27 (x+3)(x-9)
a–3 - a = a
a2 – 3ª + 2 a2 – 4ª + 3 (a+1)
m + 3m = (3m2)(1)
m2 - 1 m+1 (m+1)2(m-1)

13. 2ª - 4 = 2ª2-4ª+8
a2 – a – 6 a2 – 7ª + 12 (a-2)(a+4)
2 - 1 + 1 = 2m2-1m2
m2 – 11m + 30 m2 – 36 m2 – 25 m2-15 m2-5 m2-5
x + 2 = x +2
x2 - 5x - 14 x–7 x-7
2. Define qué es una fracción compleja y da un ejemplo.
Fracción en la que el numerador o el denominador, o ambos, contienen
fracciones.
3. Conclusiones personales sobre la unidad de fracciones algebraicas.
Herramienta útil para resolver incógnitas que se pueden aplicar en la vida diaria.

14. Define que es una ecuación lineal, los tipos que existen y cuales son los métodos de
resolución
Es una ecuación que representa una línea recta de modelo
Y=a+bx a) ordenada al origen (intersección con y)
b) pendiente (inclinación)
O bien:
Ecuación de primer grado
Ejemplo gráfico de ecuaciones lineales.
Una ecuación de primer grado o ecuación lineal es un planteamiento de igualdad,
involucrando una o más variables a la primera potencia, que no contiene productos entre
las variables, es decir, una ecuación que involucra solamente sumas y restas de una
variable a la primera potencia. En el sistema cartesiano representan rectas. Una forma
común de ecuaciones lineales es:
Donde representa la pendiente y el valor de determina la ordenada al origen (el
punto donde la recta corta al eje y).
Las ecuaciones en las que aparece el término (llamado rectangular) no son
consideradas lineales. Algunos ejemplos de ecuaciones lineales:
Tipos de ecuación lineal:

15. *Ecuación con una incógnita
♠ Todos los valores se multiplican entre si
♣ se suman o restan todos los valores con x
♥ se suman o restan todos los valores con #
♦ Se reacomodan
◊ se suman o restan según sea el caso
☺ Ejemplo:
4(2x+1)-5(x+4)+3(x-2)=7(x+3)-2x+3(x+5)
8x+4-5x-20+3x-6=7x+21-2x+3x+15
6x-22=8x+36
6x-8x=36+22
-2x=58
X=58 = -29
2

16. *Grafica de ecuaciones lineales
♠ Una ecuación se convierte en una función
♣ Tabular
☻ Ejemplo: y=3x-5
3x-5
X Y 3x-5=0 5/3=1.66
0 -5
1 -2

17. *Dos incógnitas
a) suma-resta
♠ elegir una variable para eliminar, cruzando sus coeficientes y cambiando el signo a
uno de ellos
♣ multiplicar, sumar y restar
♥ obtener el valor
♦ despejar la otra variable y sustituir el valor
☺ Ejemplo:
(-5) 2x+3y=7
(2) 5x-2y=-3
(-5) 2x+3y=7 x=7-3y=7-3x (41)
2 2 19
(2) 5x-2y=-3
-10x-15y=-35 x=5
10x -4y=-6 19
-19y=-41
Y=41
19

18. *Igualación
♠ despejar la misma variable de ambas ecuaciones
♣ igualar los despejes
♥ hacer operaciones hasta encontrar el valor de la literal
♦ sustituir en uno de los dos despejes para obtener el segundo valor
☻ Ejemplo:
4ª-3b=6 a=6+3b= 6+3(-34) =a=9
5ª+2b=-1 4 23 23
4
A=a
6+3b=-1-2b
4 5
5(6+3b)=4(-1-2b)
30+15b=-4-8b a=-1-2b=
15b+8b=-4-30 5
23b=-34
b=-34
23

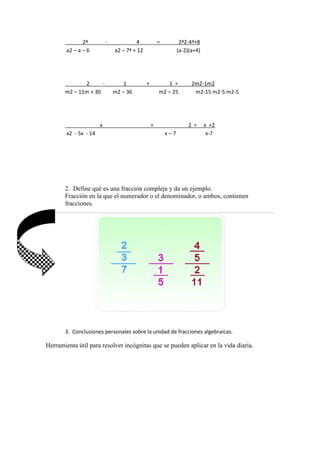
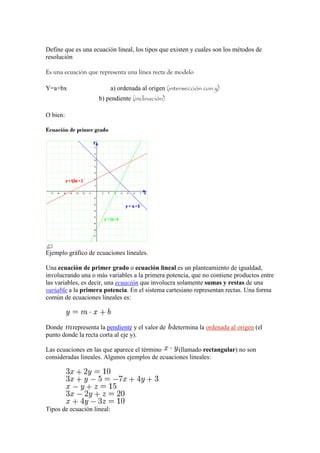
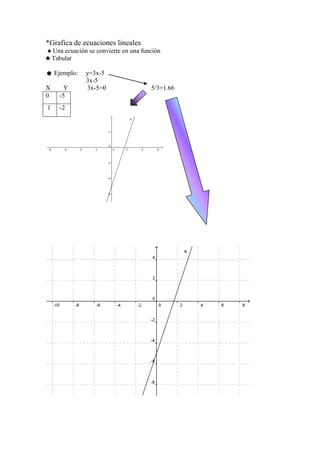
19. *Determinantes
(Regla de Cramer)
La regla de Cramer sirve para resolver sistemas de
ecuaciones lineales. Se aplica a sistemas que cumplan las dos
condiciones siguientes:
El número de ecuaciones es igual al número de incógnitas.
El determinante de la matriz de los coeficientes es distinto
de cero.
Tales s i s t e m a s se denominan s i s t e m a s de Cramer.
♠ primero se abren dos []
♣ se desmenuza la ecuación
♥ se abren dos []
♦ se multiplican
◊ se suman o restan
☺ Ejemplo:
4x-2y=7
3x+5y=-3 4 -2 7
3 5 -3 x 7 -2
(-) =35-6=29
26
∆=20+6=26 (-) -3 -5
Y 4 7
= -12-21=-33
3 -3 26
(-)

20. 2- resolver
a) 4(2x-3)+5(x-1)=7(x+2)-(3x+4)
x= 1
9
b) 5x-3+2x=x+1
4 3 2
X=30
34
c)3(4x+3)+2x-3(2-x)=2+3(x-4)+5x-2
x=9
9
d) 2x+5-3x=x+2 +3x
7 5 2
X=20
267
e)5(2x-3)+4(x+1)-5=2x-3+x
2 3
X=87
76
Graficar a), b) y c)
a) y =5x-1
b) y =2x+3
c) y =1/2x+2
a)

21. b)
c)

22. 4) dos automóviles viajan por la misma carretera; uno se encuentra delante que el otro. El de adelante va a
60km/h y el otro a 70km/h ¿Cuánto tardara el 2do automóvil en rebasar al 1ro?
R=1.16
(Un minuto dieciséis segundos)
Una joyería vende su mercancía al 50% más cara de su costo. Si vende un anillo de diamantes en $1,500
¿Cuánto pago el proveedor?
R=$1,125
Resolver las siguientes ecuaciones
a)2x-3y=4
X-4y=7
X=-5 y=10
-5 -5
b)4ª+b=6
3ª+5b=10
A= 20 b= 22
17 17
c) m-n=3
3m+4n=9 indefinido
M=21 n= 0
7 7
d) 5p+2q=-3
2p-q = 3
P=-3 q=21
9 9
e) x+2y=8
3x+5y=12
X=16 y=-12
-1 -1
f) 3m+2n=7
M-5n=-2
M= -31 n=13
17 17
g) 2h-i=-5
3h-4i=-2
H= -18 i= -11
-5 -5

23. 7) grafica los incisos a, c, e y g
a)
c)

24. e)
g)

25. 8. Se vendieron boletos para una obra de teatro escolar a $4 para adultos y $1.50 niños. Si se vendieron
1,000 boletos recaudando $3,500. ¿Cuántos boletos de cada tipo se vendieron?
X=480 niños
Y=695 adultos
9. Si se mezcla una aleación que tiene 30% de Ag con otra que contiene 55% del mismo metal
para obtener 800 kg de aleación al 40% ¿qué cantidad de cada una debe emplearse?
A=1,112gr
B=3,121gr