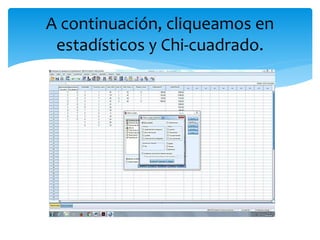
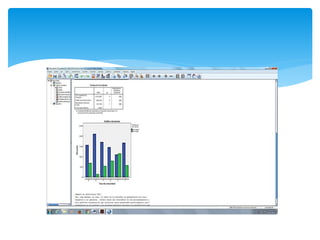
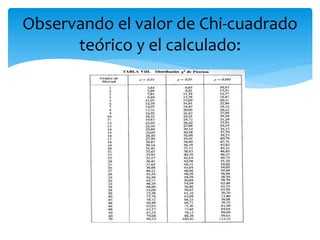
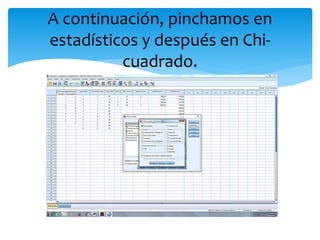
Este documento resume los pasos para realizar pruebas de chi cuadrado de homogeneidad e independencia en SPSS. Explica cómo calcular chi cuadrado para determinar si la incidencia de caries es igual en diferentes ciudades y si el sexo está relacionado con las horas de ver televisión. En ambos casos, se rechaza la hipótesis nula concluyendo que la incidencia de caries varía entre ciudades y que el sexo está asociado con el tiempo frente a la televisión.

1. Seminario 8: Chi
cuadrado.
María Soledad Robles
Cantizano.
Grupo 12 Valme.

2.  En este ejercicio de seminario vamos a mostrar como
se realiza con el programa SPSS ejercicios de Chi
cuadrado desde dos de las tres aplicaciones básicas:
 Test de homogeneidad.
 Test de independencia (realizado con tablas de
contingencia).

3. 1. Test de homogeneidad.

4.  En primer lugar tenemos que plantear las hipótesis,
para una vez obtenido el valor Chi cuadrado, saber
cual de ellas es la correcta.
 Las hipótesis serían:
 H0= Las incidencias de caries es igual en todas las
ciudades.
 H1= La incidencia de caries no es igual en todas las
ciudades.

5. Partimos de estos datos para realizar
el ejercicio .

7. En primer lugar nos disponemos a
calcular una nueva variable.

8. En este caso multiplicamos el número
total de horas por 18.

9. Como observamos en la imagen hemos
calculado el número total de horas por 18 para
así tener nuevos valores y ponderar estos.

10. Realizamos el mismo proceso con las
horas totales viendo la televisión.

12. Aquí se observa el número total de
horas multiplicado por 18.

13. A continuación, nos disponemos a calcular mediante
el test de homogeneidad Chi cuadrado.
Ponderamos el número total de niños.

15. Una vez ponderados los datos,
procedemos a obtener una tabla
cruzada y la gráfica correspondiente.

16. Colocamos las variables que deseemos en la
fila y en la columna. Después pinchamos en
mostrar gráficos de barras agrupados para
obtener el gráfico.

17. A continuación, cliqueamos en
estadísticos y Chi-cuadrado.

20.  Como podemos observar en la tabla de prueba de Chi-
cuadrado, el valor de Chi-cuadrado de Pearson es
1185,393 y el valor de significación asintótica
(bilateral) es de 0,000.
 Con estos valores podemos obtener que hipótesis
aceptamos de dos formas:
 Observando el valor de significación.
 Observando el valor de Chi-cuadrado teórico y el
calculado.
RESULTADO

21.  Hemos planteado el problema con un nivel de
confianza del 95% y un error del 5%, por lo que p=0,05.
 En la tabla de Chi-cuadrado, p=0,000.
 Como vemos, p es menor que 0,05 por lo que
aceptamos la hipótesis alternativa.
 Para concluir, podemos decir que rechazamos la
hipótesis nula, por lo que la incidencia de caries no es
igual en las seis ciudades.
Observando el valor de significación
asintótica:

22. Observando el valor de Chi-cuadrado
teórico y el calculado:

23.  Como observamos en la tabla, el valor de Chi-
cuadrado calculado es 1185,393 y el real (se observa
en la tabla mostrada en la diapositiva anterior) es
11,07.
 Como el valor de Chi-cuadrado calculado es mayor
que el valor teórico, rechazamos la hipótesis nula, es
decir, aceptamos la hipótesis alternativa.
 Concluimos diciendo que incidencia de caries no es
igual en las seis ciudades.

24. 2. Criterio de independencia.
 Planteamos las hipótesis con un nivel de confianza del
95% y un error del 5%.
 H0: El sexo es independiente de las horas de ver la
televisión.
 H1: El sexo y las horas de ver la televisión están
relacionadas.

25. En primer lugar procedemos a
ponderar los casos.

26. En este caso ponderamos el total de
horas de televisión multiplicado por
18.

27. Una vez ponderados los casos, nos
disponemos a obtener la tabla de prueba
de Chi-cuadrado y el gráfico.

28. Como en el caso anterior, ajustamos la fila y la
columna con las variables que deseemos.
Además, debemos cliquear en mostrar los
gráficos de barras agrupadas.

29. A continuación, pinchamos en
estadísticos y después en Chi-
cuadrado.

32.  Como podemos observar, el valor de Chi-cuadrado de
Pearson obtenido es 9,207 y el valor de significación
es 0,02.
 Como en el ejercicio anterior, se puede calcular de
dos formas:
 Observando el valor de p.
 Observando el valor de Chi-cuadrado teórico y el
calculado.
RESULTADO

33.  En la tabla de prueba de Chi-cuadrado, p=0,002. Como
p es menor que 0,05, aceptamos la hipótesis
alternativa.
 Por lo tanto, concluimos diciendo que rechazamos la
hipótesis nula, por lo que el sexo está asociado a las
horas de ver la televisión.
Observando el valor de significación:

34.  El valor de Chi-cuadrado obtenido es 9,207.
 El valor de Chi-cuadrado teórico es 3,84.
 Como el valor de Chi-cuadrado calculado es mayor
que el valor de Chi-teórico calculado, se rechaza la
hipótesis nula.
 Concluimos diciendo que el sexo está asociado a las
horas de ver la televisión.
Observando el valor de Chi-cuadrado
teórico y calculado: