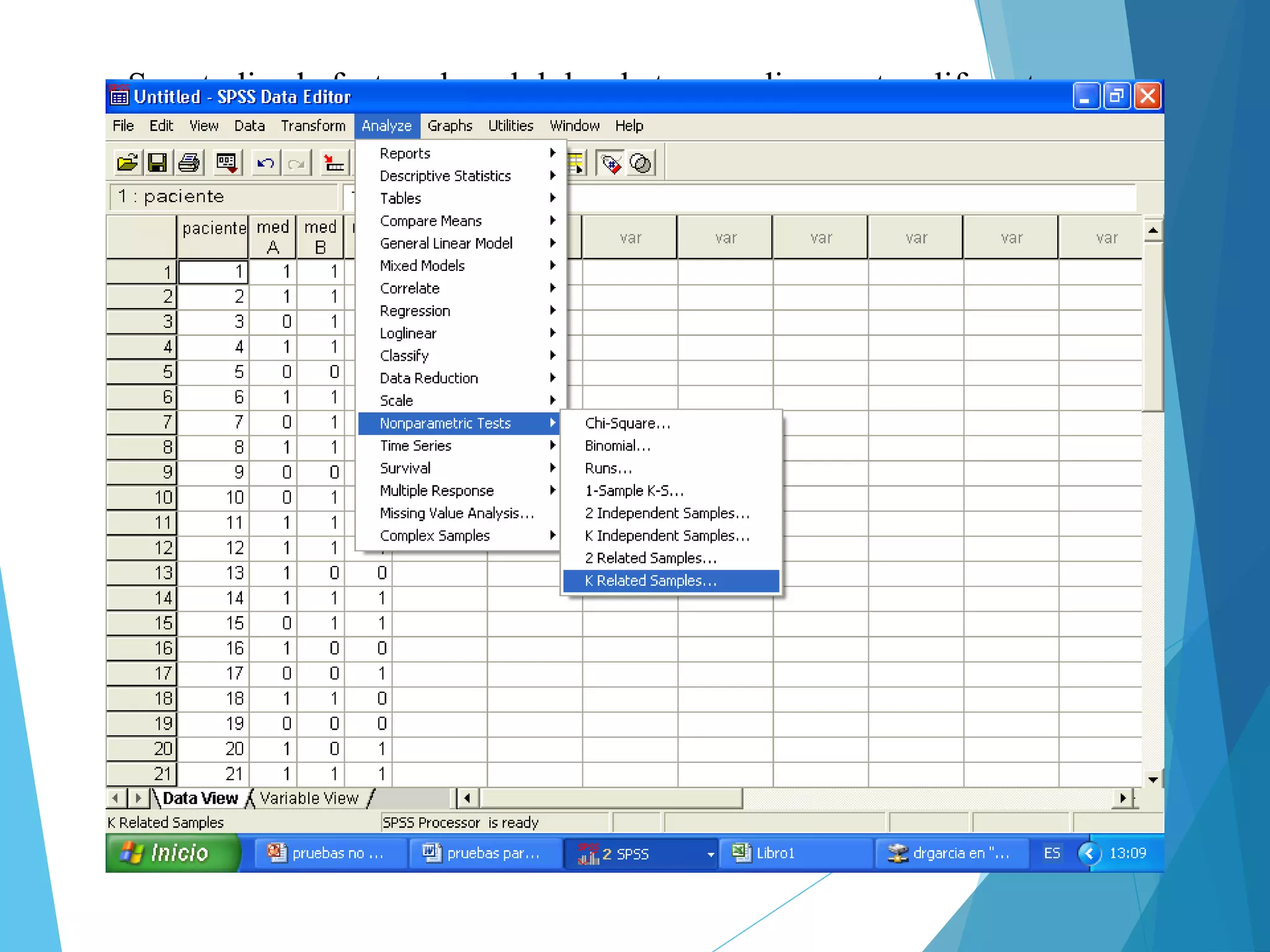
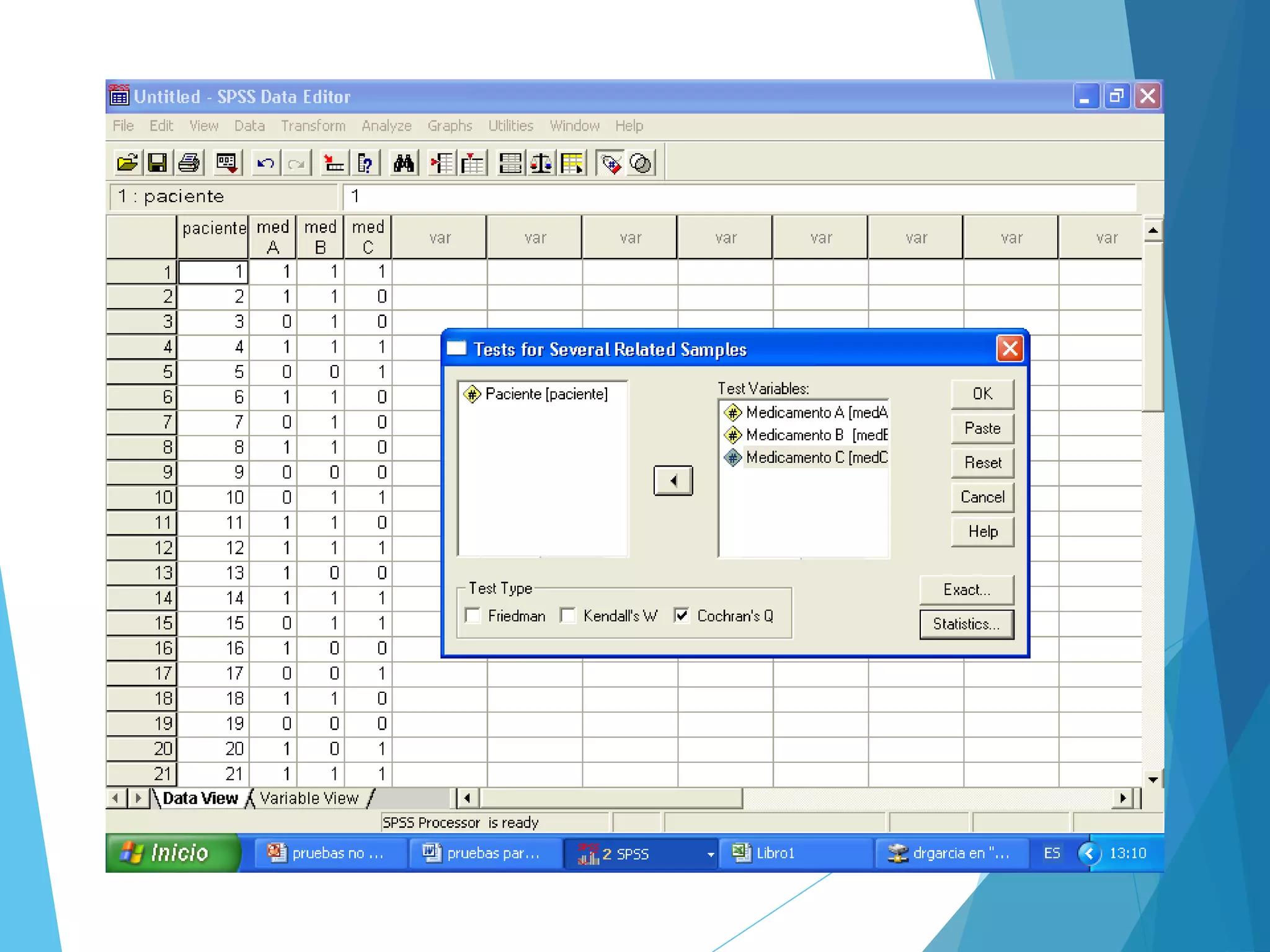
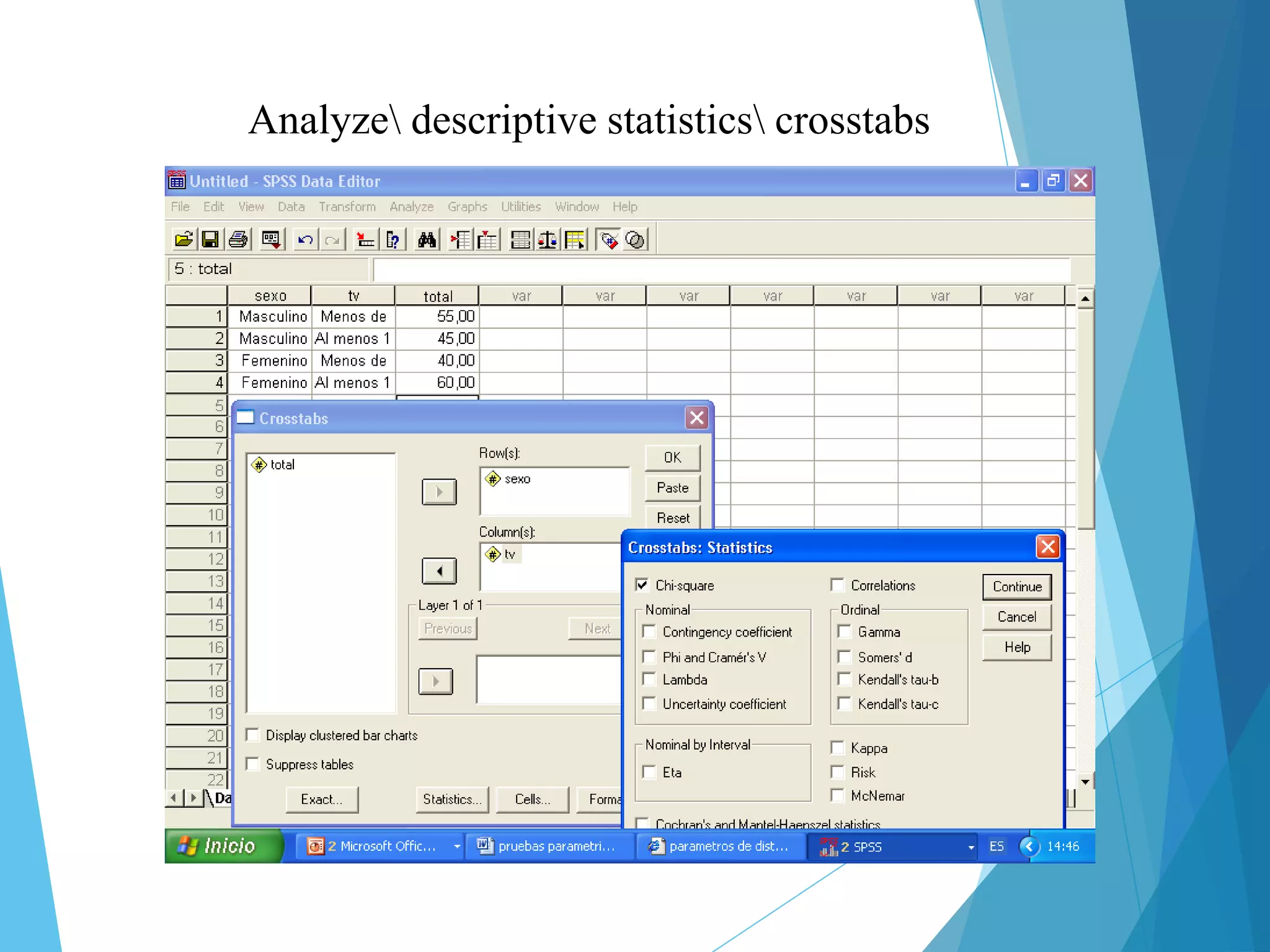
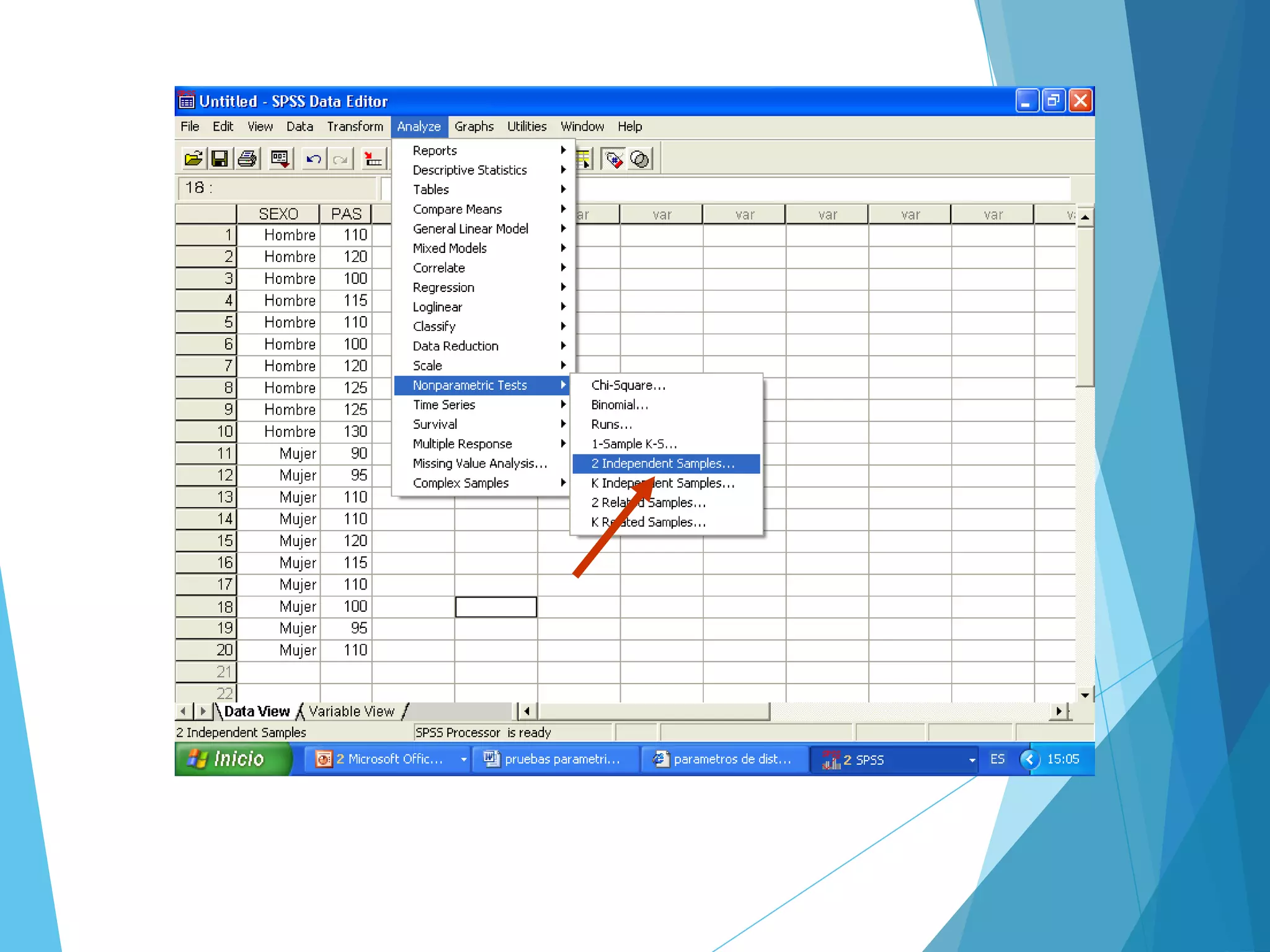
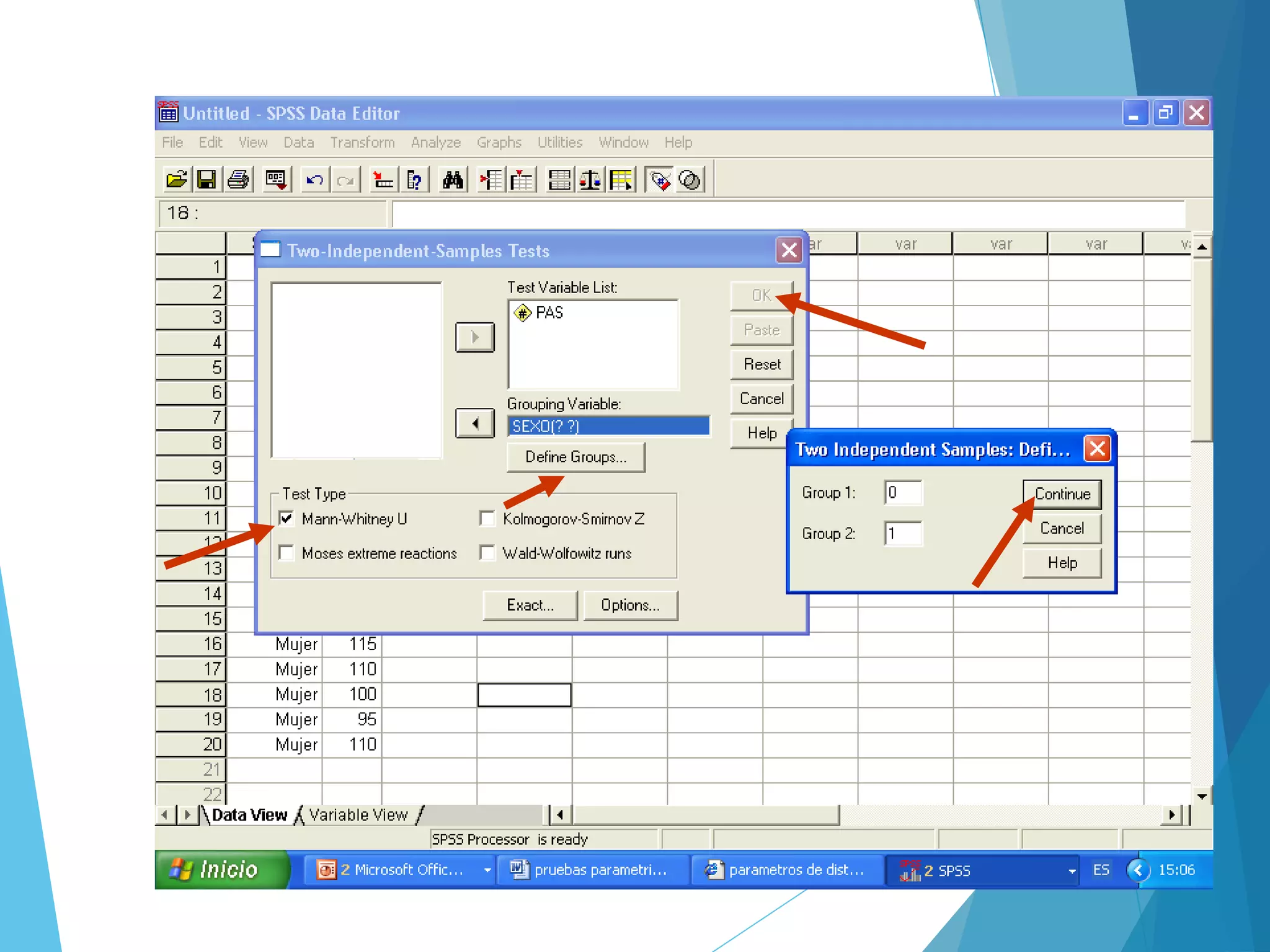
El documento analiza el uso de pruebas estadísticas no paramétricas en SPSS, comparándolas con pruebas paramétricas y describiendo cuándo es más apropiado utilizar cada tipo. Se mencionan diferentes pruebas no paramétricas como el chi cuadrado y Mann-Whitney, junto con ejemplos de aplicación en estudios de salud. También se presentan los supuestos necesarios para estas pruebas y se explican los pasos para realizar análisis de datos en situaciones específicas.

1. PRUEBAS NO
PARAMETRICAS EN
SPSS
https://www.facebook.com/asesoratesistrujillo

2. Las pruebas paramétricas asumen los
parámetros de la distribución de la
variable (media y varianza) y un tipo de
distribución normal
Las pruebas no paramétricas no asumen
acerca de los parámetros de distribución
ni se preocupa por el tipo de
distribución, sino trabajan con simple
ordenación y recuento (asignando
rankings) a los valores de la variable sin
importar la distribución.
Las pruebas estadísticas pueden ser
parametricas y no parametricas

3. Para usarlas deben cumplirse
supuestos:
Las variables tienen que ser
cuantitativas y estar medidas
en escalas de intervalo o razón
Los datos siguen una
distribución normal
Las varianzas son iguales
Muestras grandes (n > 30)
Pruebas paramétricas
A veces se usa sin cumplir los supuestos pero debe usarse con
cautela en muestras más pequeñas o con varianzas desiguales, en
estos casos prefiera usar pruebas No paramétricas

4. Se deben usar con:
Datos de distribución libre (no necesariamente normal). Si
un grupo tiene distribución normal mientras el otro no.
Si se trata de datos cuantitativos, ordinales o nominales
Con varianza grande, un grupo con varianza 0 y el otro no
Al trabajar con muestras pequeñas.
Pruebas no paramétricas

5. Las pruebas
paramétricas
tienen más poder
de contraste y
pueden analizar
interacciones
entre variables
independientes
¿ QUÉ VENTAJAS TIENEN LAS PRUEBAS
PARAMETRICAS SOBRE LAS NO
PARAMETRICAS?

6. PRUEBAS NO PARAMETRICAS
Chi cuadrado de Pearson (independencia,
bondad de ajuste, homogeneidad)
Prueba exacta de Fischer
U de mann Whitney – W de Wilcoxon
T de Wilcoxon
Mac Nemar
Kruskall Wallis
Friedman
Q de Cochran

7. ELECCIÓN DE LA PRUEBA NO PARAMETRICA
1 muestra
2 muestras
Más de 2
muestras
Relacionadas
independientes
independientes
Relacionadas
Cualitativa
Cuantitativa
Cuantitativa y cualitativa
Chi cuadrado
U de mann
Whitney
Mc Nemar
Cuantitativa Friedman
Cualitativa Q de Cochran
Cuantitativa Kruskal Wallis
Cuantitativa Wilcoxon
Binomial

8.  



F
i
C
j ij
ijij
CF
E
EO
1 1
2
)1)(1(
2 )(

CHI CUADRADO DE PEARSON
Prueba de bondad de ajuste
Ho: La muestra se ajusta a una distribución teorica
(esperado o modelo)
H1: Ho: La muestra no se ajusta a una distribución
teorica (esperado o modelo)
Analyze / non parametric test/ chi square

9.  



F
i
C
j ij
ijij
CF
E
EO
1 1
2
)1)(1(
2 )(

CHI CUADRADO DE PEARSON
Criterio de homogeneidad
Ho= Las poblaciones son homogeneas
Ho= Las poblaciones no son homogeneas
Analyze/ descriptive statisticts/ crosstabs

10.  



F
i
C
j ij
ijij
CF
E
EO
1 1
2
)1)(1(
2 )(

CHI CUADRADO DE PEARSON
Criterio de independencia
Ho: Las variable son independientes
H1: Las variable estan relacionadas
Analyze/ descriptive statisticts/ crosstabs

11. Un estudio sobre caries dental en niños de seis ciudades con diferentes cantidades
de fluor en el suministro de agua, ha proporcionado los resultados siguientes:
H0: Las incidencia de caries es igual en las seis ciudades (las poblaciones son homogeneas)
H1: Las incidencia de caries no es igual en las seis ciudades (las poblaciones no son
homogeneas)
Comunidad Nº niños sin caries Nº niños con caries
A 38 87
B 8 117
C 30 95
D 44 81
E 64 61
F 32 93
Chi cuadrado: homogeneidad de poblaciones

12. Data weight cases
Cargar de esta manera los resultados, al hacer weight cases se esta
consiguiendo que la tabla se despliegue como una base de datos completa a
partir del cual se han resumido los datos en la tabla

13. Analyze descriptive statistics crosstabs

14. Case Processing Summary
750 100,0% 0 ,0% 750 100,0%grupo * caries
N Percent N Percent N Percent
Valid Missing Total
Cases
grupo * caries Crosstabulation
Count
38 87 125
8 117 125
30 95 125
44 81 125
64 61 125
32 93 125
216 534 750
A
B
C
D
E
F
grupo
Total
sin caries con caries
caries
Total
Chi-Square Tests
65,855a
5 ,000
72,153 5 ,000
12,860 1 ,000
750
Pearson Chi-Square
Likelihood Ratio
Linear-by-Linear
Association
N of Valid Cases
Value df
Asymp. Sig.
(2-sided)
0 cells (,0%) have expected count less than 5. The
minimum expected count is 36,00.
a.
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0
H0: Las incidencia de caries es igual en las seis ciudades
H1: Las incidencia de caries no es igual en las seis ciudades
Conclusiòn: La incidencia de caries es igual en las 6 ciudades (poblaciones homogeneas)
Chi cuadrado (homogeneidad)

15. CHI CUADRADO (CRITERIO DE INDEPENDENCIA)
Una muestra aleatoria de 200 adultos se clasifican de acuerdo al sexo y al
número de horas que miran televisión durante la semana las frecuencias se
dan en la siguiente tabla:
Menos de 15 horas Al menos 15 horas
Hombre 55 45
Mujer 40 60
Nº de horas que miran TV
Con esta información, ¿se puede concluir que el tiempo utilizado para ver tv es
independiente del sexo? use α= 0.05
Ho : El sexo es independiente de las horas de ver televisión
H1 : El sexo y las horas de ver televisión estan relacionadas

16. Data weight cases

17. Analyze descriptive statistics crosstabs

18. Case Processing Summary
200 100,0% 0 ,0% 200 100,0%sexo * tv
N Percent N Percent N Percent
Valid Missing Total
Cases
sexo * tv Crosstabulation
Count
40 60 100
55 45 100
95 105 200
Femenino
Masculino
sexo
Total
Menosde
15 horas
Al menos
15 horas
tv
Total
Chi-Square Tests
4,511b
1 ,034
3,930 1 ,047
4,529 1 ,033
,047 ,024
4,489 1 ,034
200
Pearson Chi-Square
Continuity Correctiona
Likelihood Ratio
Fisher's Exact Test
Linear-by-Linear
Association
N of Valid Cases
Value df
Asymp. Sig.
(2-sided)
Exact Sig.
(2-sided)
Exact Sig.
(1-sided)
Computed only for a 2x2 tablea.
0 cells (,0%) have expected count less than 5. The minimum expected count is
47,50.
b.
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0
H0: El sexo es independiente de las horas de mirar TV
H1: El sexo esta asociado a las horas de mirar TV
Conclusiòn: El sexo de la persona esta asociado al tiempo que mira TV, las mujeres
permanecen màs tiempo mirando TV
Chi cuadrado (independencia)

19. Comparar 2 grupos independientes y que no
tienen distribución normal o que sean ordinales
Paralela a la prueba parametrica de contraste t
para muestras independientes
Contrasta si dos poblaciones muestreadas son
equivalentes en su posición
Es recomendable pero no imprescindible que las
poblaciones comparadas tengan el mismo tamaño
U DE MANN WHITNEY - WILCOXON

20. PAS
Hombres
Rango 1
(R1)
Orden PAS
Mujeres
Rango 2
(R2)
Orden
110
120
100
115
110
100
120
125
125
130
9.5
16
5
13.5
9.5
5
16
18.5
18.5
20
7
15
4
13
8
5
16
18
19
20
90
95
110
110
120
115
110
100
95
110
1
2.5
9.5
9.5
16
13.5
9.5
5
2.5
9.5
1
2
9
10
17
14
11
6
3
12
Total 131.5 78.5
Se desea saber si hay diferencias entre presión arterial
sistólica de hombres y mujeres

21. Estos valores de U y U´se contrastan con los valores de la tabla
para la U de Mann Withney y en el cual tiene valores para alfa
bilateral al 0.05 y alfa unilateral para 0.01 y se eligen según los
valores caen en el área de rechazo o no rechazo de Ho
U DE MANN WHITNEY


 1
2
)1( 11
21 R
nn
nnU 

 2
2
)1(
´ 22
21 R
nn
nnU
U U´
Area de
rechazo
Area de
rechazoArea de no rechazo

24. Ranks
10 7,85 78,50
10 13,15 131,50
20
SEXO
Mujer
Hombre
Total
PAS
N Mean Rank Sum of Ranks
Test Statisticsb
23,500
78,500
-2,039
,041
,043
a
Mann-Whitney U
Wilcoxon W
Z
Asymp. Sig. (2-tailed)
Exact Sig. [2*(1-tailed
Sig.)]
PAS
Not corrected for ties.a.
Grouping Variable: SEXOb.
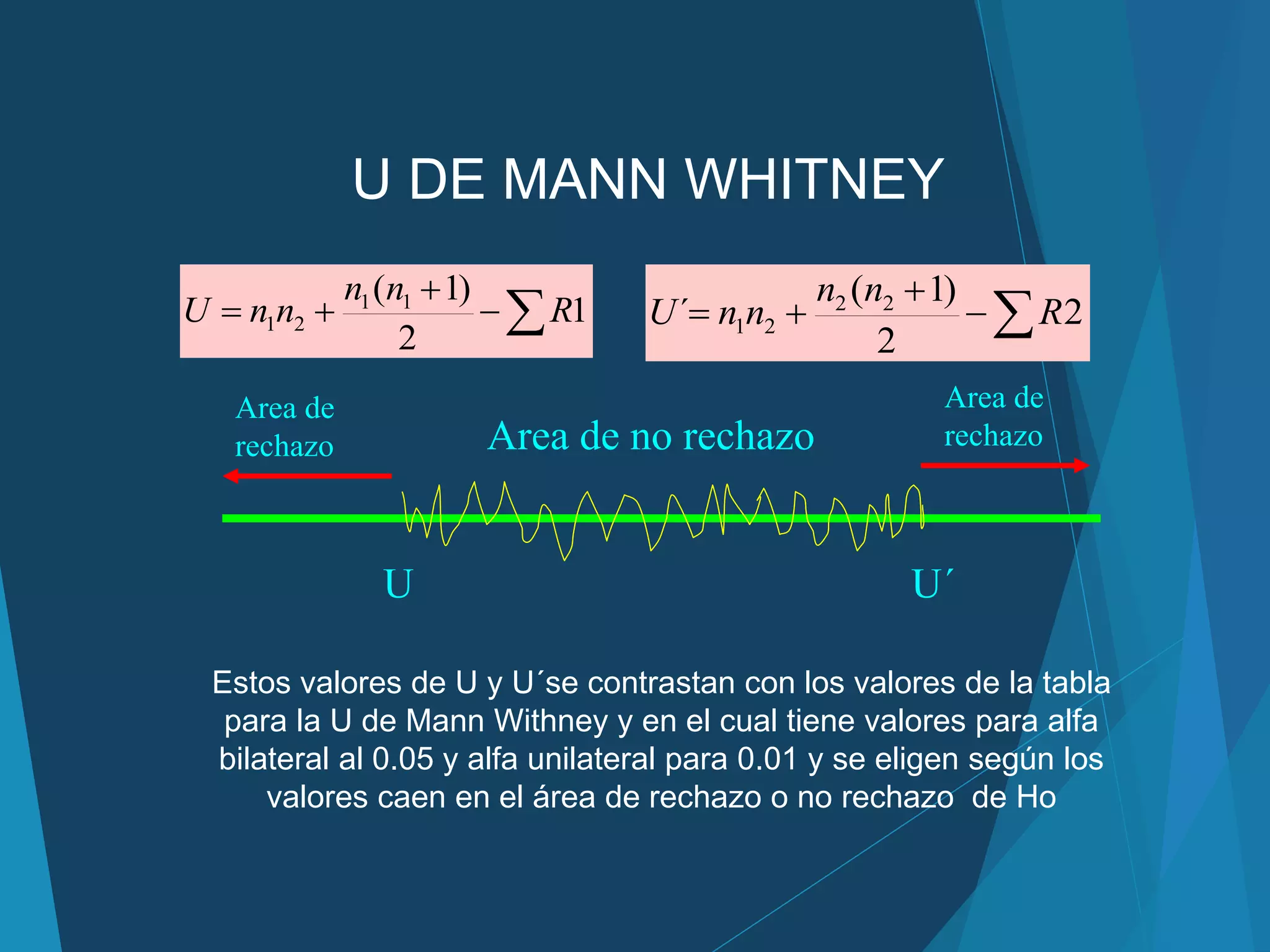
U´
U
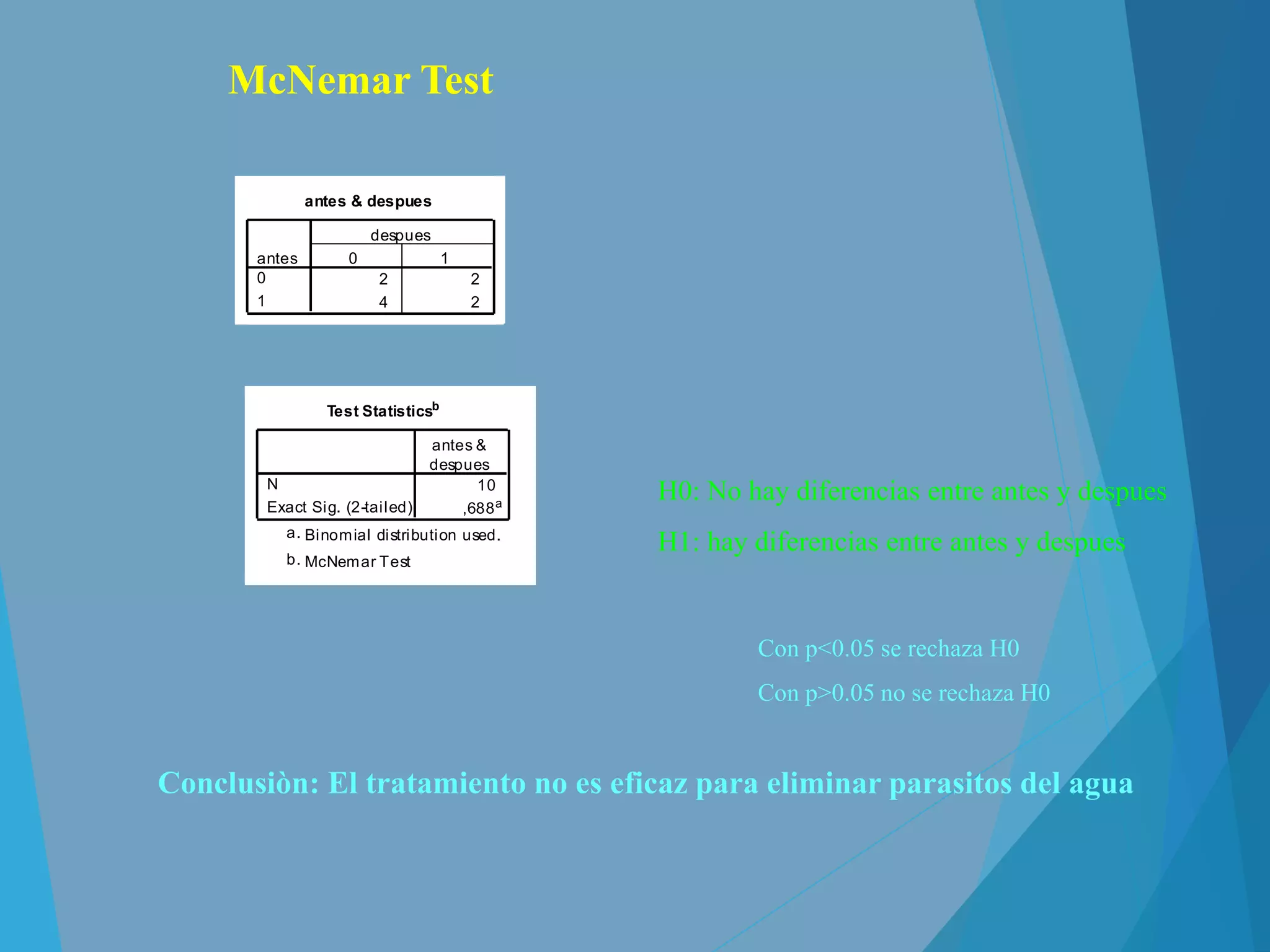
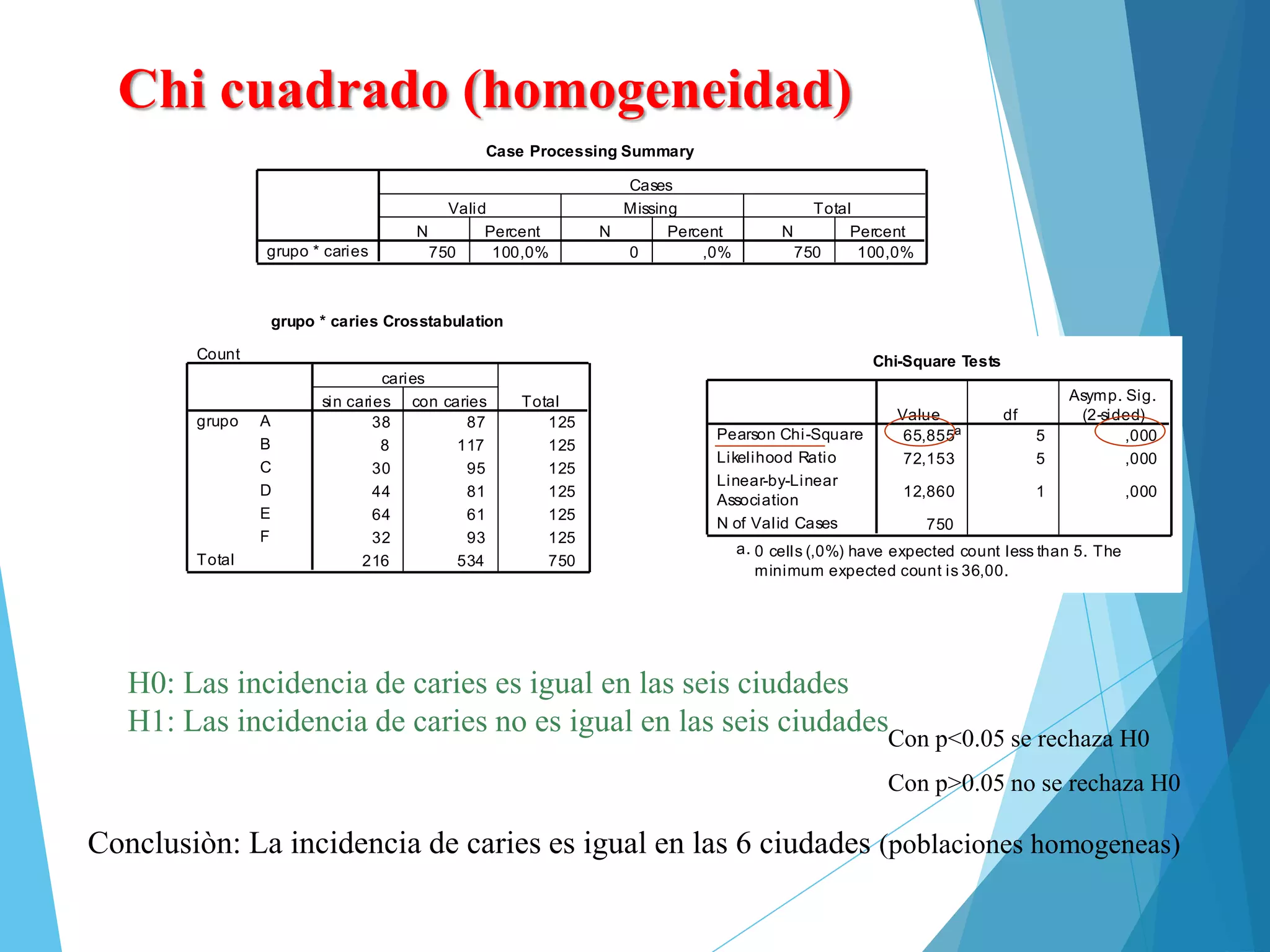
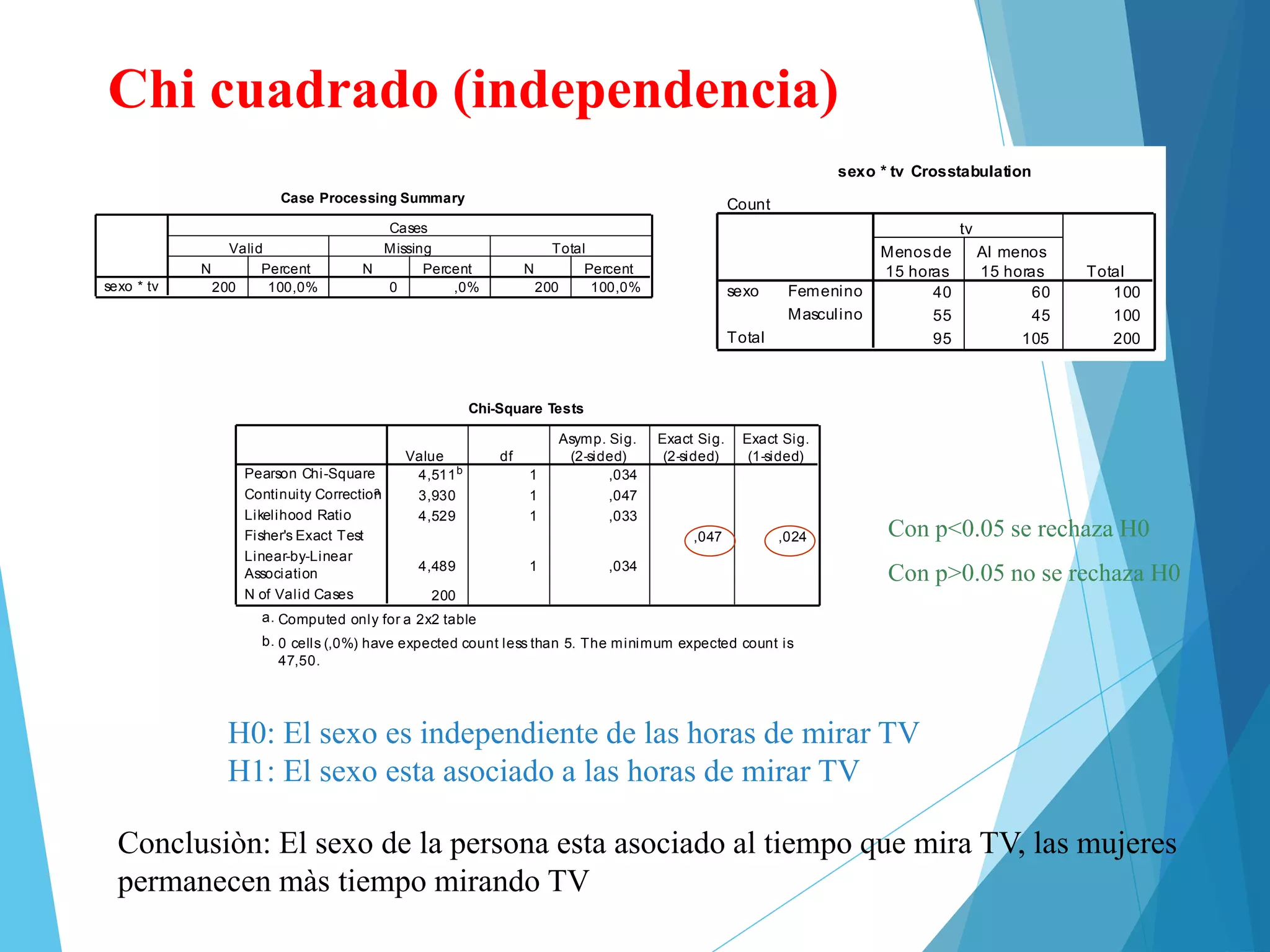
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0
H0: La presion arterial sistolica es igual en hombres y en mujeres
H1: La presion arterial sistolica no es igual en hombres y en mujeres
N
ranksofSum
rankMean 
El ranking promedio de mujeres esta en 7.85 y el de hombres esta en 13.15, es
decir hay diferencias entre hombres y mujeres y como p<0.05 se rechaza H0
Conclusiòn: La PAS es diferente en hombres y en mujeres siendo mayor en
hombres.
n
RU
Zu
u


σu tiene una formula compleja

25. Comparar 2 grupos relacionados y variables
cuantitativas que no tienen distribución normal o
que sean ordinales
Paralela a la prueba parametrica de contraste t
para muestras relacionadas
Contrasta si dos poblaciones muestreadas son
equivalentes en su posición
Es recomendable pero no imprescindible que las
poblaciones comparadas tengan el mismo tamaño
T DE WILCOXON

26. Peso
inicial
Peso
final
Diferencia Rango
+ s
Rango
-s
Orden
80
70
68
75
72
85
90
75
85
80
75
68
68
70
74
60
75
70
80
79
-5
-2
0
-5
2
-25
-15
-5
-5
-1
2.5
5.5
2.5
5.5
9
8
5.5
5.5
1
4
2
--
5
3
9
8
6
7
1
Total 2.5 42.50
Para ubicar en ranking se procede ignorando el signo de la diferencia
Pacientes que intentan bajar de peso sometiéndose a una dieta, se desea
saber si hay diferencias antes y después de la dieta

29. Wilcoxon Signed Ranks Test
Ranks
8a
5,31 42,50
1b 2,50 2,50
1c
10
Negative Ranks
Positive Ranks
Ties
Total
pesofin - pesoin
N Mean Rank Sum of Ranks
pesofin < pesoina.
pesofin > pesoinb.
pesofin = pesoinc.
Test Statisticsb
-2,393a
,017
Z
Asymp. Sig. (2-tailed)
pesofin -
pesoin
Based on positive ranks.a.
Wilcoxon Signed Ranks Testb.
H0: peso final = peso final
H1: peso final ≠ peso final
H0: peso final > peso final
H1: peso final ≤ peso final
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0
Conclusiòn la dieta es efectiva para bajar de peso

30. Se estudia la presencia de parásitos en el agua antes y después de un
procedimiento para eliminar parásitos. ¿Es ùtil el procedimiento?
COMPARACION DE 2 GRUPOS RELACIONADOS CON
VARIABLES DICOTOMICAS
Prueba de signos y prueba de Mc Nemar
Antes Después
+
+
+
-
-
+
-
+
-
+
-
+
-
+
-
-
-
+
+
-

32. Sign Test
Frequencies
4
2
4
10
Negative Differencesa
Positive Differencesb
Tiesc
Total
despues - antes
N
despues < antesa.
despues > antesb.
despues = antesc.
Test Statisticsb
,688aExact Sig. (2-tailed)
despues -
antes
Binomial distribution used.a.
Sign Testb.
H0: No hay diferencias entre antes y despues
H1: hay diferencias entre antes y despues
Conclusiòn: El tratamiento no es eficaz para eliminar parasitos del agua
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0

33. Inicial Final
+ -
+ A B
- C D
 
cb
cb



2
(1)
2
1
NemarMcdeχ
 
1666.0
6
1
24
124
NemarMcdeχ
2
(1)
2





34. McNemar Test
antes & despues
2 2
4 2
antes
0
1
0 1
despues
Test Statisticsb
10
,688a
N
Exact Sig. (2-tailed)
antes &
despues
Binomial distribution used.a.
McNemar Testb.
H0: No hay diferencias entre antes y despues
H1: hay diferencias entre antes y despues
Conclusiòn: El tratamiento no es eficaz para eliminar parasitos del agua
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0

35. Comparar k grupos independientes y variables
cuantitativas que no tienen distribución normal o
que sean ordinales
Paralela a la prueba parametrica de ANOVA para
muestras indpendientes
Contrasta si K poblaciones muestreadas son
equivalentes en su posición
Es recomendable pero no imprescindible que las
poblaciones comparadas tengan el mismo tamaño
KRUSKALL WALLIS

36. Grupo Reaccion Grupo Reaccion Grupo Reaccion
1 10 2 10 3 15
1 10 2 15 3 20
1 11 2 15 3 12
1 8 2 12 3 10
1 7 2 12 3 9
1 15 2 10 3 15
1 14 2 12 3 18
1 10 2 14 3 17
1 9 2 9 3 12
1 10 2 14 3 16
Se esta midiendo la reacciòn frente a un medicamento en
tres grupos de personas ¿Se desea saber si hay diferencias
entre los tiempos de reacciòn entre los 3 grupos

38. Kruskal-Wallis Test
Ranks
10 10,00
10 15,80
10 20,70
30
Grupo
1
2
3
Total
Tiempo de reacciòn
N Mean Rank
Test Statisticsa,b
7,579
2
,023
Chi-Square
df
Asymp. Sig.
Tiempo de
reacciòn
Kruskal Wallis Testa.
Grouping Variable: Grupob.
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0
H0: La reaccion frente al medicamento
es igual en los 3 grupos
H1: La reaccion frente al medicamento
no es igual en los 3 grupos
Conclusiòn: Hay diferencias entre los 3 grupos para
reaccionar frente al medicamento administrado

39. Comparar K grupos relacionados y variables
cuantitativas que no tienen distribución normal o
que sean ordinales
Paralela a la prueba parametrica de ANOVA para
muestras relacionadas
Contrasta si K poblaciones muestreadas son
equivalentes en su posición
Es recomendable pero no imprescindible que las
poblaciones comparadas tengan el mismo tamaño
FRIEDMAN

40. Paciente Droga A Droga B Droga C
1 10 10 15
2 10 15 20
3 11 15 12
4 8 12 10
5 7 12 9
6 15 10 15
7 14 12 18
8 10 14 17
9 9 9 12
10 10 14 16
Se esta midiendo la reacciòn de 10 pacientes frente a tres
medicamento diferentes ¿Se desea saber si hay diferencias
entre los tiempos de reacciòn frente a los 3 medicamentos?

43. Descriptive Statistics
10 10,4000 2,45855 7,00 15,00
10 12,3000 2,16282 9,00 15,00
10 14,4000 3,56526 9,00 20,00
Droga A
Droga B
Droga C
N Mean Std. Deviation Minimum Maximum
Ranks
1,35
2,00
2,65
Droga A
Droga B
Droga C
Mean Rank
Test Statisticsa
10
9,135
2
,010
N
Chi-Square
df
Asymp. Sig.
Friedman Testa.
Friedman Test
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0
H0: La de los accion de los 3 medicamento
sobre la reaciòn de los pacientes es igual
H1: La de los accion de los 3 medicamento
sobre la reaciòn de los pacientes no es igual
Conclusiòn: Hay diferencias en la accion de los 3
medicamentos sobre la reacciòn de los pacientes

44. Comparar K grupos relacionados y variables
cualitativas dicotomicas
Paralela a la prueba de Mc Nemar para muestras
relacionadas
Contrasta si K poblaciones muestreadas son
equivalentes en su posición
Es recomendable pero no imprescindible que las
poblaciones comparadas tengan el mismo tamaño
Q DE COCHRAN

45. Pacient
e
Med A Med B Med C Pacient
e
Med A Med B Med C Pacient
e
Med A Med B Med C
1 1 1 1 10 0 1 1 18 1 1 0
2 1 1 0 11 1 1 0 19 0 0 0
3 0 1 0 12 1 1 1 20 1 0 1
4 1 1 1 13 1 0 0 21 1 1 1
5 0 0 1 14 1 1 1 22 0 1 0
6 1 1 0 15 0 1 1 23 1 1 0
7 0 1 0 16 1 0 0 24 1 0 1
8 1 1 0 17 0 0 1 25 0 1 1
9 0 0 0 25 pacientes reciben 3 medicamentos para mejorar su tos
0 = mejora su tos 1 = no mejora su tos

46. Pacien
te
Medic
A
Medic
C
Medic
B
1 1 1 1
2 1 1 0
3 0 1 0
4 1 1 1
5 0 0 1
6 1 1 0
7 0 1 0
8 1 1 0
9 0 0 0
10 0 1 1
11 1 1 0
12 1 1 1
13 1 0 0
Pacien
te
Medic
A
Medic
C
Medic
B
14 1 1 1
15 0 1 1
16 1 0 0
17 0 0 1
18 1 1 0
19 0 0 0
20 1 0 1
21 1 1 1
22 0 1 0
23 1 1 0
24 1 0 1
25 0 1 1
Se estudia el efecto sobre el dolor de tres medicamentos diferentes en
25 pacientes (0=no calma 1= si calma) ¿Se desea saber si hay
diferencias entre el efecto de los 3 medicamentos?

48. Descriptive Statistics
25 ,60 ,500 0 1
25 ,68 ,476 0 1
25 ,48 ,510 0 1
Medicamento A
Medicamento B
Medicamento C
N Mean Std. Deviation Minimum Maximum
Frequencies
10 15
8 17
13 12
Medicamento A
Medicamento B
Medicamento C
0 1
Value
Cochran Test
Test Statistics
25
2,111a
2
,348
N
Cochran's Q
df
Asymp. Sig.
1 is treated as a success.a.
H0: No hay diferencias entre los 3
medicamentos para mejorar mejorar la tos
H1: hay diferencias entre los 3
medicamentos para mejorar mejorar la tos
Conclusiòn: No hay diferencia estadisticamente significativa entre los
3 medicamentos para mejorar la tos en los pacientes.
Con p<0.05 se rechaza H0
Con p>0.05 no se rechaza H0

49. asesoramitesis@hotmail.com
https://www.facebook.com/asesoratesistrujillo