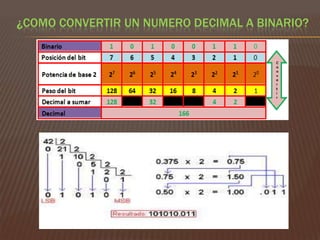
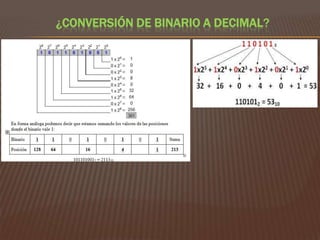
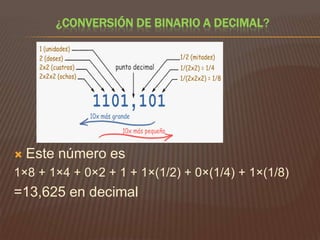
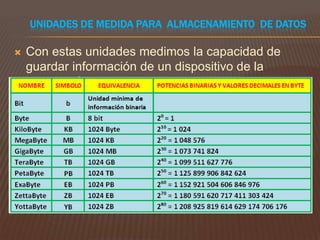
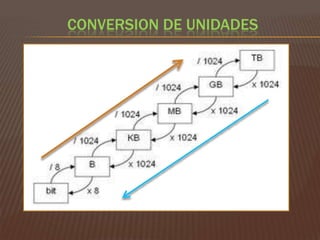
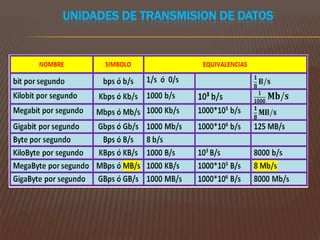
El documento explica los sistemas de numeración, centrándose en el sistema decimal y el binario. Describe cómo cada sistema utiliza la base de sus dígitos para determinar el valor en función de su posición, así como las conversiones entre los dos sistemas. También aborda las unidades de medida en informática relacionadas con almacenamiento, procesamiento y transmisión de datos.

1. ¿QUE ES EL SISTEMA DE NUMERACION?
Conjunto de símbolos y reglas que se utilizan
para la representación de datos numéricos o
cantidades.
 Su característica principal es la base, que es el
número de símbolos distintos que utiliza y
además es el coeficiente que determina cuál es
el valor de cada símbolo dependiendo la
posición relativa que ocupe.
 Los sistemas de numeración actuales son
sistemas posicionales, que se caracterizan
porque un símbolo tiene distinto valor según
la posición que ocupa en la cifra


2. SISTEMA DE NUMERACIÓN DECIMAL

Utilizado habitualmente, se compone de diez
símbolos o dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9) a
los que otorga un valor dependiendo de la
posición que ocupen en la cifra: unidades,
decenas, centenas, millares, etc.
 El valor de cada dígito está asociado al de una
potencia de base 10, número que coincide con
la cantidad de símbolos o dígitos del sistema
decimal, y un exponente igual a la posición que
ocupa el dígito menos uno, contando desde la
derecha.

3. SISTEMA DE NUMERACIÓN DECIMAL

En el sistema decimal el número 528, por
ejemplo, significa:
 5 centenas + 2 decenas + 8 unidades, es
decir:
 5*102 + 2*101 + 8*100 o, lo que es lo mismo:
 500 + 20 + 8 = 528

4. SISTEMA DE NUMERACION BINARIO

Utiliza sólo dos dígitos, el 1 y 0 , los cuales
representan dos niveles de voltaje, alto y bajo.
 Cuando leas un número binario, pronuncia cada
dígito (por ejemplo, el número binario "101" se
lee "uno cero uno"). De esta manera la gente no
los confunde con números decimales.
 Un dígito binario por sí solo se llama "bit". Por
ejemplo 11010 tiene cinco bits de longitud.
 ¿Cómo indicar que un número está en
binario?
 Para mostrar que un número es binario,
ponemos un pequeño 2 detrás: 101

5. SISTEMA DE NUMERACION BINARIO

En una cifra binaria, cada dígito tiene distinto
valor dependiendo de la posición que ocupe.
 El valor de cada posición es el de una
potencia de base 2, elevada a un exponente
igual a la posición del dígito menos uno. Se
puede observar que la base de la potencia
coincide con la cantidad de dígitos utilizados
(2) para representar los números.

6. SISTEMA DE NUMERACION BINARIO

De acuerdo con estas reglas, el número
binario 1011 tiene un valor que se calcula así:
3
2
1
0
1*2 + 0*2 + 1*2 + 1*2 , es decir:
8 + 0 + 2 + 1 = 11
 Para expresar que ambas cifras describen la
misma cantidad lo escribimos así:
10112 = 1110

7. ¿COMO CONVERTIR UN NUMERO DECIMAL A BINARIO?


Basta con realizar divisiones sucesivas por 2 y
escribir los restos obtenidos en cada división en
orden inverso al que han sido obtenidos.
Por ejemplo, para convertir al sistema binario el
número 10010 haremos una serie de divisiones que
arrojarán los restos siguientes:
Si tomamos los
restos en orden
inverso
obtenemos la cifra
binaria: 10010 =
11001002

8. ¿COMO CONVERTIR UN NUMERO DECIMAL A BINARIO?

9. ¿CONVERSIÓN DE BINARIO A DECIMAL?
Hay que desarrollar el número, teniendo en
cuenta el valor de cada dígito (peso) en su
posición, que es el de una potencia de 2,
cuyo exponente es 0 en el bit situado más a
la derecha, y se incrementa en una unidad
según vamos avanzando posiciones hacia la
izquierda.
 Por ejemplo, para convertir el número binario
10100112 a decimal, lo desarrollamos
teniendo en cuenta el valor de cada bit:


1*26 + 0*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 83

10. ¿CONVERSIÓN DE BINARIO A DECIMAL?


11. ¿CONVERSIÓN DE BINARIO A DECIMAL?

Este número es
1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8)
=13,625 en decimal

12. EL TAMAÑO DE LAS CIFRAS BINARIAS
La cantidad de dígitos necesarios para
representar un número en el sistema binario es
mayor que en el sistema decimal.
 En el ejemplo anterior, para representar el
número 10010, que en el sistema decimal está
compuesto por tres dígitos, se requieren 7
dígitos en binario.
 ¿Cuántos dígitos se requieren como mínimo
para representar al 255?
 Para representar al 255 se necesitarán ocho
dígitos, porque 28 = 256 y podemos afirmar, por
tanto, que 255 es el número más grande que
puede representarse con ocho dígitos.


13. ¿Cuantos numeros decimales se pueden representar
con n digitos binarios?

Como regla general, con n dígitos binarios
n
pueden representarse un máximo de 2 ,
números.
 ¿ Cual es el numero decimal mas grande que
puede representarse con n dígitos binarios?
 El número más grande que puede escribirse
con n dígitos es una unidad menos, es decir,
n
2 – 1.
 Con cuatro bits, pueden representarse un
4
total de 16 números, porque 2 = 16 y el mayor
4
de dichos números es el 15, porque 2 -1 = 15.

14. EL TAMAÑO DE LAS CIFRAS BINARIAS

Averigua cuántos números pueden
representarse con 8, 10, 16 y 32 bits y cuál
es el número más grande que puede
escribirse en cada caso.
Dados dos números binarios:
01001000 y 01000100
 ¿Cuál de ellos es el mayor?
 ¿Podrías compararlos sin necesidad de
convertirlos al sistema decimal?


15. VALOR POSICIONAL DE LOS DÍGITOS
Según la posición que ocupan cada uno de
los dígitos se dice que tiene mayor o menor
peso. Denominándose el de mayor peso
con las siglas MSB (Most Significant Bit) y la
de menor peso, LSB (Least Significant Bit).
 Teniendo mayor peso aquel dígito que se
encuentra más a la izquierda y siendo el de
menor peso el que se encuentra más a la
derecha.


16. UNIDADES DE MEDIDA EMPLEADAS EN INFORMATICA

Podemos agrupar estas medidas en tres
grupos:

Almacenamiento

Procesamiento

Transmisión de datos.

17. UNIDADES DE MEDIDA PARA ALMACENAMIENTO DE DATOS

Con estas unidades medimos la capacidad de
guardar información de un dispositivo de la
computadora.

18. CONVERSION DE UNIDADES

19. UNIDADES DE TRANSMISION DE DATOS

20. CONVERSION DE KBs a Kbs
Podemos calcular esa velocidad de transmisión
(para pasarla a Kbps o Kilobits por segundo)
simplemente multiplicando el dato que se nos
muestra por 8.
 Ejemplo, una trasmisión que se nos indica
como de 308 KB/s corresponde a una
velocidad de transmisión de 2.464 Kbps, a lo
que es lo mismo, 2.64 Mbps. Esta conversión
nos es muy útil para comprobar la velocidad
real de nuestra línea ADSL, por ejemplo, ya que
la velocidad de esta si que se expresa en Kbps
o en Mbps


21. UNIDADES DE MEDIDA DE PROCESAMIENTO
La velocidad de procesamiento de un
procesador se mide en megahercios (MHZ) ó
gigahercios (GHZ).
 Un megahercio es igual a un millón de hercios.
el gigahercio, es igual a1.000 millones de
hercios por segundo.
 Un hercio (herz) es una unidad de frecuencia
que equivale a un ciclo o repetición de un
evento por segundo.
 Esto, significa que un procesador que trabaje a
una velocidad de 500 megahercios es capaz de
repetir 500millones de ciclos por segundo.


22. UNIDADES DE MEDIDA DE PROCESAMIENTO