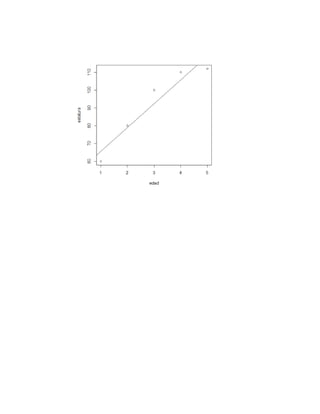
El documento presenta varios ejercicios de aplicación sobre regresión lineal. El primer ejercicio compara medidas manuales y automáticas de la concentración de nitratos en un lago, encontrando una alta correlación positiva entre los métodos. El segundo ejercicio estudia la relación entre el número de cuadrados dentro de cuadrados dibujados y el tamaño de su lado, hallando una relación lineal.

1. Ejercicios de aplicación
Ejercicio 1
Para estudiar el efecto de las aguas residuales de las alcantarillas que afluyen a
un lago, se toman medidas de la concentración de nitrato en el agua. Para
monitorizar la variable se ha utilizado un antiguo método manual. Se idea un
nuevo método automático. Si se pone de manifiesto una alta correlación positiva
entre las medidas tomadas empleando los dos métodos, entonces se hará uso
habitual del método automático. Los datos obtenidos son los siguientes:
Manual = X 25 40 120 75 150 300 270 400 450 575
Automático = Y 30 80 150 80 200 350 240 320 470 583
Comprobar la idoneidad del modelo lineal de regresión. Si el modelo es apropiado,
hallar la recta de regresión de Y sobre X y utilizarla para predecir la lectura que se
obtendría empleando la técnica automática con una muestra de agua cuya lectura
manual es de 100. Realizar el ejercicio en R

2. SOLUCIÓN EN R
Manual=read.table("manual.txt",header=T)
attach(Manual)
Manual
manual automatico
1 25 30
2 40 80
3 120 150
4 75 80
5 150 200
6 300 350
7 270 240
8 400 320
9 450 470
10 575 583
regresion=lm(automatico~manual,data=Manual)
summary(regresion)
Call:
lm(formula = automatico ~ manual, data = Manual)
Residuals:
Min 1Q Median 3Q Max
-78.98 -18.57 14.31 23.53 44.24
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 26.11496 21.20188 1.232 0.253
manual 0.93216 0.07064 13.195 1.04e-06 ***

3. ---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1
‘ ’ 1
Residual standard error: 40.11 on 8 degrees of freedom
Multiple R-squared: 0.9561, Adjusted R-squared:
0.9506
F-statistic: 174.1 on 1 and 8 DF, p-value: 1.036e-06
R2 = 0.9561 el modelo lineal es adecuado

4. Ejercicio 2
Sobre una hoja de papel cuadriculado dibuje aproximadamente 5 cuadrados de
diversos tamaños.
a. ¿Cuántos cuadritos encierra cada uno de los cuadrados dibujados?.
Represente esta variable mediante la letra N
b. ¿Cuánto mide el lado de cada cuadrado?. Represente esta variable mediante
la letra L
c. Coleccione su información en una tabla de datos.
d. ¿Existe alguna relación entre una y otra variable?. Detalle su respuesta.
Represente las parejas (L,N) en un plano cartesiano
e. ¿Qué clase de curva obtiene?
a.
N 1 4 9 16 25
b.
L 1 2 3 4 5
c.
N 1 4 9 16 25
L 1 2 3 4 5
d.
SOLUCIÓN EN R
Cuadros=read.table("cuadros.txt",header=T)
attach(Cuadros)
Cuadros

5. cuadros centimetros
1 1 1
2 4 2
3 9 3
4 16 4
5 25 5
regresion=lm(centimetros~cuadros,data=Cuadros)
summary(regresion)
Call:
lm(formula = centimetros ~ cuadros, data = Cuadros)
Residuals:
1 2 3 4 5
-0.3957 0.1230 0.3209 0.1979 -0.2460
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.23529 0.25559 4.833 0.01689 *
cuadros 0.16043 0.01827 8.783 0.00311 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1
‘ ’ 1
Residual standard error: 0.3532 on 3 degrees of freedom
Multiple R-squared: 0.9626, Adjusted R-squared:
0.9501
F-statistic: 77.14 on 1 and 3 DF, p-value: 0.003109

6. plot(Cuadros)
abline(lm(centimetros~cuadros))
Ejercicio 3
A partir de las siguientes observaciones para 5 años de las variables X e Y,
ajústese el modelo de regresión de Y en función de X más idóneo. Donde:
Y: producción nacional de un subsector industrial, en millones de toneladas.
X: tiempo
Año X Y
1995
1996
1997
1998
1999
1
2
3
4
5
1,25
5
11,25
20
30,5

7. Ejercicio 4
Cinco niñas de 2,4, 6,7 y 8 años pesan respectivamente 15, 19, 25, 38, y 34
kilogramos respectivamente, entonces una niña de 12 años pesara
aproximadamente:
A. 45
B. 55
C. 15
D. 51
E. 61
SOLUCIÓN EN R
Niñas=read.table("niñas.txt",header=T)
attach(Niñas)
Niñas
niñas pesos
1 2 15
2 4 19
3 6 25
4 7 38
5 8 34
regresion=lm(pesos~niñas,data=Niñas)
summary(regresion)
Call:
lm(formula = pesos ~ niñas, data = Niñas)
Residuals:

8. 1 2 3 4 5
1.491 -1.974 -3.440 5.828 -1.905
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.0431 5.1936 1.164 0.329
niñas 3.7328 0.8933 4.178 0.025 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1
‘ ’ 1
Residual standard error: 4.303 on 3 degrees of freedom
Multiple R-squared: 0.8534, Adjusted R-squared:
0.8045
F-statistic: 17.46 on 1 and 3 DF, p-value: 0.02497
Y = 3,7328X + 6,0431
Y = 3,7328 (12) + 6,0431
Y = 50,8367
Ejercicio 5
En el análisis de Regresión lineal se puede afirmar todo lo siguiente excepto:
A. Ajusta los datos a una línea recta
B. Predice valores de una variable si se conoce el valor de la otra
C. Establece una relación cuantitativa entre dos variables relacionadas

9. D. El método gráfico para determinar la relación entre dos variables es más
concreto que el método matemático o de mínimos cuadrados
E. Una relación lineal entre dos variables queda representada por una línea recta
llamada ecuación de regresión
Ejercicio 6
Dado Los siguientes datos expuestos en la tabla
La fórmula de regresión para los datos propuestos está dada por:
A. y = 11,5x + 67,5 B. y = 7,5x + 85,5 C. y = 13,4x + 52,2
D. y = 14,4x + 47 E. y = 14x + 48,8
SOLUCIÓN EN R
Estatura=read.table("estatura.txt",header=T)
attach(Estatura)
Estatura
edad estatura
1 1 60
2 2 80
3 3 100
4 4 110
5 5 112
regresion=lm(estatura~edad,data=Estatura)
summary(regresion)
Edad 1 2 3 4 5
Estatura 60 80 100 110 112

10. Call:
lm(formula = estatura ~ edad, data = Estatura)
Residuals:
1 2 3 4 5
-5.6 1.0 7.6 4.2 -7.2
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.200 7.650 6.824 0.00644 **
edad 13.400 2.307 5.810 0.01015 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1
‘ ’ 1
Residual standard error: 7.294 on 3 degrees of freedom
Multiple R-squared: 0.9184, Adjusted R-squared:
0.8912
F-statistic: 33.75 on 1 and 3 DF, p-value: 0.
Ejercicio 7
El Grafico para los puntos dispersos está dado por:

11. SOLUCIÓN EN R
Estatura=read.table("estatura.txt",header=T)
attach(Estatura)
Estatura
plot(Estatura)
0
20
40
60
80
100
120
0 1 2 3 4 5
0
20
40
60
80
100
120
0 1 2 3 4 5
0
20
40
60
80
100
120
0 1 2 3 4 5
0
20
40
60
80
100
120
0 1 2 3 4 5
A
B
C D

12. Ejercicio 8
El diagrama de dispersión para la regresión lineal está dado por
SOLUCIÓN EN R
Estatura=read.table("estatura.txt",header=T)
attach(Estatura)
Estatura
plot(Estatura)
abline(lm(estatura~edad))
0
20
40
60
80
100
120
0 1 2 3 4 5
0
20
40
60
80
100
120
0 1 2 3 4 5
A B
0
20
40
60
80
100
120
0 1 2 3 4 5
0
20
40
60
80
100
120
0 1 2 3 4 5
C
D