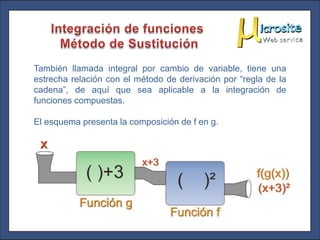
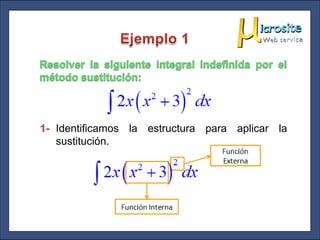
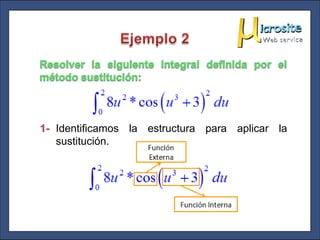
El documento describe el método de integración por sustitución. Este método se aplica a funciones compuestas y está relacionado con la regla de la cadena para derivación. El proceso implica identificar la estructura de la función, realizar una sustitución de variable, integrar con respecto a la nueva variable y volver a expresar el resultado en términos de la variable original.

1. Desarrollado por
Esp. Oscar Ardila Chaparro

2. También llamada integral por cambio de variable, tiene una
estrecha relación con el método de derivación por “regla de la
cadena”, de aquí que sea aplicable a la integración de
funciones compuestas.
El esquema presenta la composición de f en g.

3. Para introducir la formula y las características de una integral
susceptible de aplicar el método de sustitución, empezamos
por recordar la regla de la cadena para la derivación. En la
definición se resalta en verde lo que de ahora en adelante
notaremos como función interna.
Aplicando la integral en ambos lados de la igualdad y
simplificando tenemos.

4. La identificación de la siguiente estructura será el primer paso
para la aplicación del método de integración por sustitución. En
rojo se resalta la anti derivada (integral) de f´(x).
Cabe resaltar que esta estructura puede presentarse de forma explicita o
implícita, y en este ultimo caso requeriremos de algunas
transformaciones o arreglos matemáticos para realizar la sustitución.

5. 1- Identificamos la estructura para aplicar la
sustitución.

6. 2- Planteamos la sustitución considerando.
De esta manera tenemos para la integral:

7. 3- Realizando la sustitución:
4- Realizamos la nueva integral en términos de u:
5- Y volvemos nuevamente a establecer nuestra
respuesta (en naranja) en términos de la
variable original:

8. 1- Identificamos la estructura para aplicar la
sustitución.

9. 2- Planteamos la sustitución.

10. 3- La integral posee limites por lo cual es necesario
un cambio de los mismos antes de plantear la
nueva integral en términos de u.
4- De esta manera planteamos la nueva integral:

11. 5- Solucionamos la nueva integral como sigue:
6- Evaluando finalmente la integral:

13. Esperamos que esta información oriente un poco tu proceso de
familiarización con el entorno y el seguimiento de cursos en
plataforma.
Desarrollado por
Esp. Oscar Ardila Chaparro