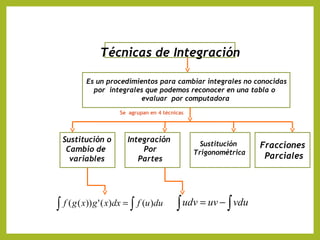
El documento detalla técnicas de integración en matemáticas, incluyendo integración por partes, sustitución y sustitución trigonométrica. Se busca que los estudiantes comprendan y apliquen estas técnicas para resolver problemas matemáticos complejos. Además, se proporciona una introducción a las integrales definidas y ejemplos prácticos para facilitar su entendimiento.

1. Universidad laica Eloy Alfaro de
Manabí
• Integrantes
•
Echeverría Suarez Oswaldo Javier
•
Mero Moreira Cristhian Javier
•
Mero Pico Máximo Alexander
•
Párraga Guadamú Carlos
•
Paz Gutiérrez Luis Eduardo
•
Pico Zambrano Miguel Ángel
•
Pin Macías Cristóbal clemente
•
Posligua rivera Jefferson Rafael
•
Santos Alcívar Jean Carlos
•
Tumbaco Bailón Klever Alexander
•
Ureta Navarrete Leonela Estefanía

2. índice
índice
• Introducción
Introducción
objetivos
Técnica de
integración
Integración por
parte
Integración por
Sustitución
trigonométrica
Integrales
definida
• Objetivo general
• Objetivo específico
• Técnica de integración
• Integración por parte
• Método de Integración por sustitución o cambio de variable
• Integrales Definidas

3. Introducción
• A manera de introducción se puede decir que los
temas ya mencionado son muy útil en la aplicación
de la resolución de problemas matemáticos, es por
eso, que como estudiantes universitario debemos
manejar este tipo de técnica que ayudan a que el
estudiante, resuelva sin dificultad ejercicios
propuestos por los docentes.
• Por lo cual a continuación daremos a conocer los
temas ya mencionado.

4. Objetivo general
Que el estudiante conozca y sea capaz de resolver problemas
matemáticos en donde use como herramienta la técnica de
integración por partes, por sustitución trigonométricas e
Integración definidas.
• Objetivo específicos:
•
Que el estudiante distinga las técnica de integración y haga
uso de ella en la resolución de problemas.
Que el estudiante comparta en base a su conocimiento lo
aprendido durante su nivel académico.

5. Técnicas de integración
¿Cómo reconocer cuál técnica
emplear para integrar ?
Desarrollaremos técnicas que
nos permitirán emplear las
fórmulas básicas con objeto de
llegar a integrales indefinidas
de funciones más complicadas

6. Técnicas de Integración
Es un procedimientos para cambiar integrales no conocidas
por integrales que podemos reconocer en una tabla o
evaluar por computadora
Se agrupan en 4 técnicas
Sustitución o
Cambio de
variables
Integración
Por
Partes
Sustitución
Trigonométrica
∫ f ( g ( x)) g ' ( x)dx = ∫ f (u )du ∫ udv = uv − ∫ vdu
Fracciones
Parciales

7. Método de Integración por partes

8. Método de Integración por partes

9. Método de Integración por partes

10. INTEGRACION POR PARTES
• ¿Será cierto que ……….
¿ ∫ f ( x) g ( x)dx = ∫ f ( x)dx ∫ g ( x)dx ?
La regla del producto establece que si f y g
son funciones diferenciables,
d
[ f ( x) g ( x)] = f ′( x) g ( x) + f ( x) g ′( x)
dx
∫ f ′( x) g ( x)dx + ∫ f ( x) g ′( x)dx = f ( x) g ( x)

11. Reordenando la expresión anterior se tiene la fórmula de
integración por partes
Es decir:
∫ f ( x) g ′( x)dx = f ( x) g ( x) − ∫ f ′( x) g ( x)dx
Sean u = f (x) y v = g (x) entonces du = fI(x)dx y
dv = gI(x)dx, así, según la regla de sustitución, la
fórmula de integración por partes se transforma en:
udv = uv − ∫ vdu
∫

12. Método de Integración por sustitución
o cambio de variable
La regla de sustitución para integrar corresponde
a la regla de la cadena para diferenciar.
Debemos tener presente que si
U = g (x), entonces d u = g I (x) dx

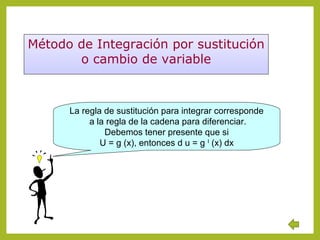
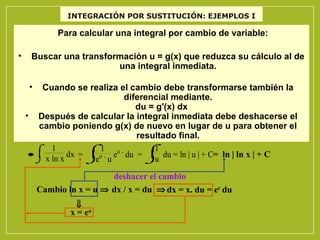
13. INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE
Si F es una primitiva de f, y g es derivable se tiene:
(F o g)'(x) = F '[g(x)] g'(x) = f[g(x)] g'(x)
Que con la notación de integrales se escribe:
⌠
 f[g(x)]g'(x) dx = F[g(x)] + C
⌡
Si se escribe u = g(x), entonces du = g' (x) dx. Con esta sustitución se tiene
⌠

⌡
f(u) du = F(u) + C

14. INTEGRACIÓN POR SUSTITUCIÓN: EJEMPLOS I
Para calcular una integral por cambio de variable:
•
Buscar una transformación u = g(x) que reduzca su cálculo al de
una integral inmediata.
•
Cuando se realiza el cambio debe transformarse también la
diferencial mediante.
du = g'(x) dx
• Después de calcular la integral inmediata debe deshacerse el
cambio poniendo g(x) de nuevo en lugar de u para obtener el
resultado final.
1
⌠ 1
⌠
⌠1
•  x ln x dx =  . eu . du =  du = ln | u | + C= ln | ln x | + C
u
u
e
⌡
⌡
⌡ u
deshacer el cambio
Cambio ln x = u ⇒ dx / x = du ⇒ dx = x. du = et du
⇓
x = eu

15. Integración por sustitución: Ejemplos II
⌠3


⌡
•x
1⌠
1 4
1⌠ 3 4
1 u1/2
3
 u du =
x + 2 dx = 
4x x + 2 dx =4
+ C = 4 (x + 2) + C
4
41
⌡
⌡
+1
2
4
Cambio x4 + 2 = u ⇒ 4x3 . dx = du
deshacer el cambio
1
1⌠ 3.
1 t4
• sen 2x cos 2x dx =  t dt =
=
sen4 2x + C
+C
8
2
2 4
⌡
⌠


⌡
3
.
Cambio sen 2x = t ⇒ 2 cos 2x . dx = dt
deshacer el cambio

16. Integración de funciones trigonométricas
En el caso de funciones trigonométricas son precisas, en ocasiones,
transformaciones trigonométricas, que las pasan a funciones cuya
integración es ya conocida o son más simples.
Son útiles las sustituciones:
sen x = t
cos x =t
tg x =t
tg x/2=t

17. Integración de funciones trigonométricas

18. INTEGRACION POR SUSTITUCION
TRIGONOMETRICA
• Este método, el cual es un caso especial de cambio de variable, nos permitirá integrar cierto tipo de funciones algebraicas cuyas integrales indefinidas son funciones trigonométricas.
• Por ejemplo:

19. Las sustituciones que involucran funciones trigonométricas se pueden llevar
a cabo en aquellas integrales cuyo integrando contiene una expresión de la
forma:
La sustitución trigonométrica permite transformar una integral en otra que
contiene funciones trigonométricas cuyo proceso de integración es más
sencillo.
Las formulas principales para este tipo de integración son las
siguientes

20. Integrales definidas
Definición:
Sea f una función que ha sido definida en un intervalo cerrado [a,b]. Si
existe
Se dice que f es integrable en [a,b]. Además la llamada integral definida
(o integral de Riemann) de f entre a y b es el valor
b
n
∫ f ( x)dx = Lim ∑ f (ε
a
P →0
k =1
k
)( xk − xk −1 )

21. Bibliografías
 http://www.slideshare.net/search/slideshow?
searchfrom=header&q=integracion+por+sustitucion
 http://es.wikipedia.org/wiki/M%C3%A9todos_de_integraci%C3%B3n
 http://matematica1.com/category/integracion-por-sustitucion-trigonométrica/
 El Cálculo, Louis Leithold, Oxford University Press, 1998.
Matemáticas para Administración y Economía, Ernest Haeussler, Richard Paul,
Pearson Prentice Hall, Décimo Segunda Edición, 2008.