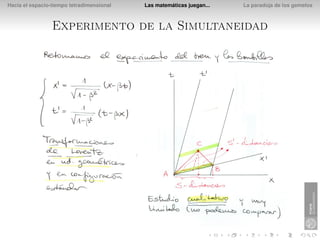
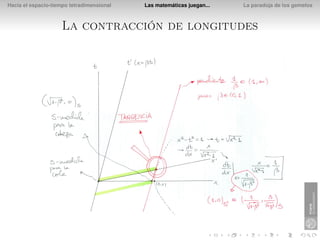
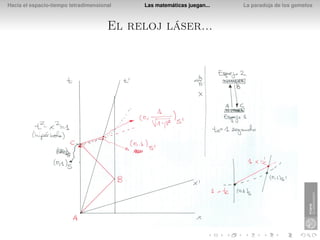
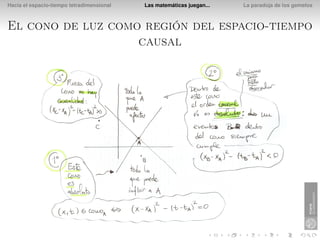
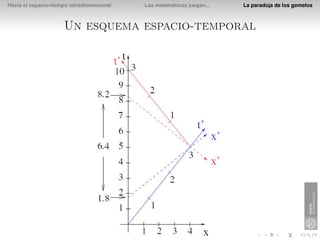
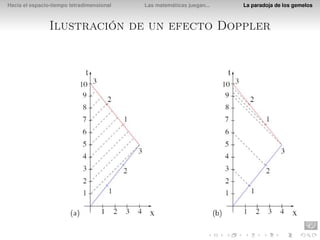
El documento presenta la paradoja de los gemelos en la relatividad especial. Explica que si Diana viaja a una estrella a una velocidad del 80% de la luz, el tiempo que pasa para ella en el viaje es de 3 años, mientras que su hermano gemelo Apolo que se queda en la Tierra verá que pasan 5 años. Esto se debe a que los relojes y las longitudes se ven afectados por la velocidad relativa en la relatividad especial.

1. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Hacia la relatividad especial (y III)
José Antonio Pastor González
CPR de Cehegín
Lunes 7 de noviembre de 2011
La geometría del espacio-tiempo:
una introducción al pensamiento de Albert Einstein

2. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Contenidos
1 Hacia el espacio-tiempo tetradimensional
2 Las matemáticas juegan...
3 La paradoja de los gemelos

3. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Contenidos
1 Hacia el espacio-tiempo tetradimensional
2 Las matemáticas juegan...
3 La paradoja de los gemelos

4. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Unidades geométricas

5. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Consecuencias de estas unidades

6. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Una nueva visión de las transformaciones

7. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Contenidos
1 Hacia el espacio-tiempo tetradimensional
2 Las matemáticas juegan...
3 La paradoja de los gemelos

8. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Experimento de la Simultaneidad

9. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
La aparición del intervalo como algo
absoluto

10. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
¿Cómo calibrar los ejes?

11. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Calibración de los ejes

12. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
La contracción de longitudes

13. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
El reloj láser...

14. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Causas antes que efectos... o efectos antes
que causas

15. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Una primera solución

16. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
El cono de luz como región del espacio-tiempo
causal

17. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Contenidos
1 Hacia el espacio-tiempo tetradimensional
2 Las matemáticas juegan...
3 La paradoja de los gemelos

18. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Planteamiento inicial
Diana y Apolo son dos hermanos gemelos aunque Diana
es más viajera y quiere visitar la estrella α-centauro
Planifican el viaje; la nave de Diana es capaz de viajar a
0, 8c y la distancia Tierra-Estrella es de 4 años-luz.
Cuando en la Tierra (en el sistema Tierra-Estrella-Apolo)
hayan pasado 5 años Diana estará en su destino
Primera pregunta: ¿qué tiempo transcurre para Diana en
ese viaje?

19. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Planteamiento inicial
Diana y Apolo son dos hermanos gemelos aunque Diana
es más viajera y quiere visitar la estrella α-centauro
Planifican el viaje; la nave de Diana es capaz de viajar a
0, 8c y la distancia Tierra-Estrella es de 4 años-luz.
Cuando en la Tierra (en el sistema Tierra-Estrella-Apolo)
hayan pasado 5 años Diana estará en su destino
Primera pregunta: ¿qué tiempo transcurre para Diana en
ese viaje?

20. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Planteamiento inicial
Diana y Apolo son dos hermanos gemelos aunque Diana
es más viajera y quiere visitar la estrella α-centauro
Planifican el viaje; la nave de Diana es capaz de viajar a
0, 8c y la distancia Tierra-Estrella es de 4 años-luz.
Cuando en la Tierra (en el sistema Tierra-Estrella-Apolo)
hayan pasado 5 años Diana estará en su destino
Primera pregunta: ¿qué tiempo transcurre para Diana en
ese viaje?

21. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la primera
Sea A el suceso Diana sale de la Tierra y B el suceso
Diana llega a la Estrella
Según Apolo (sistema Tierra-Estrella) han pasado 5 años
en su reloj entre A y B. Pero Apolo quiere saber cuánto
marca el reloj que Diana lleva en su nave. Como éste está
en movimiento respecto de Apolo, la lectura (5) que hace
Apolo de la separación temporal entre A y B está dilatada
con respecto a la de Diana (<5)
Conclusión: el viaje desde el punto de vista de Diana dura
menos. ¿Cuánto? Pues el dado por t0 donde
t0
=5
1 − β2
Así t0 = 3 que es el tiempo que mide Diana en su reloj

22. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la primera
Sea A el suceso Diana sale de la Tierra y B el suceso
Diana llega a la Estrella
Según Apolo (sistema Tierra-Estrella) han pasado 5 años
en su reloj entre A y B. Pero Apolo quiere saber cuánto
marca el reloj que Diana lleva en su nave. Como éste está
en movimiento respecto de Apolo, la lectura (5) que hace
Apolo de la separación temporal entre A y B está dilatada
con respecto a la de Diana (<5)
Conclusión: el viaje desde el punto de vista de Diana dura
menos. ¿Cuánto? Pues el dado por t0 donde
t0
=5
1 − β2
Así t0 = 3 que es el tiempo que mide Diana en su reloj

23. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la primera
Sea A el suceso Diana sale de la Tierra y B el suceso
Diana llega a la Estrella
Según Apolo (sistema Tierra-Estrella) han pasado 5 años
en su reloj entre A y B. Pero Apolo quiere saber cuánto
marca el reloj que Diana lleva en su nave. Como éste está
en movimiento respecto de Apolo, la lectura (5) que hace
Apolo de la separación temporal entre A y B está dilatada
con respecto a la de Diana (<5)
Conclusión: el viaje desde el punto de vista de Diana dura
menos. ¿Cuánto? Pues el dado por t0 donde
t0
=5
1 − β2
Así t0 = 3 que es el tiempo que mide Diana en su reloj

24. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la segunda
La contracción de longitudes está dada por la fórmula
= 0 1 − β2
En este caso, 0 = 4 años/luz, pero desde el punto de vista
de Diana ocurre que
= 4 × 0, 6 = 2, 4 años/luz
Como la velocidad sigue siendo β = 0, 8, entonces el
tiempo empleado por Diana es
2, 4/0, 8 = 3 años

25. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la segunda
La contracción de longitudes está dada por la fórmula
= 0 1 − β2
En este caso, 0 = 4 años/luz, pero desde el punto de vista
de Diana ocurre que
= 4 × 0, 6 = 2, 4 años/luz
Como la velocidad sigue siendo β = 0, 8, entonces el
tiempo empleado por Diana es
2, 4/0, 8 = 3 años

26. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la segunda
La contracción de longitudes está dada por la fórmula
= 0 1 − β2
En este caso, 0 = 4 años/luz, pero desde el punto de vista
de Diana ocurre que
= 4 × 0, 6 = 2, 4 años/luz
Como la velocidad sigue siendo β = 0, 8, entonces el
tiempo empleado por Diana es
2, 4/0, 8 = 3 años

27. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la tercera
Transformaciones de Lorentz para Apolo (sistema S) y
Diana (sistema S’) nos dan lo siguiente:
El suceso A tiene coordenadas (0, 0)S y (0, 0)S
El suceso B tiene coordenadas (4, 5)S y (0, 3)S
Para S se tiene tB − tA = 5 mientras que para S se
cumple tB − tA = 3
Curiosidad: observemos que el intervalo espacio-temporal
es invariante

28. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la tercera
Transformaciones de Lorentz para Apolo (sistema S) y
Diana (sistema S’) nos dan lo siguiente:
El suceso A tiene coordenadas (0, 0)S y (0, 0)S
El suceso B tiene coordenadas (4, 5)S y (0, 3)S
Para S se tiene tB − tA = 5 mientras que para S se
cumple tB − tA = 3
Curiosidad: observemos que el intervalo espacio-temporal
es invariante

29. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la tercera
Transformaciones de Lorentz para Apolo (sistema S) y
Diana (sistema S’) nos dan lo siguiente:
El suceso A tiene coordenadas (0, 0)S y (0, 0)S
El suceso B tiene coordenadas (4, 5)S y (0, 3)S
Para S se tiene tB − tA = 5 mientras que para S se
cumple tB − tA = 3
Curiosidad: observemos que el intervalo espacio-temporal
es invariante

30. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la tercera
Transformaciones de Lorentz para Apolo (sistema S) y
Diana (sistema S’) nos dan lo siguiente:
El suceso A tiene coordenadas (0, 0)S y (0, 0)S
El suceso B tiene coordenadas (4, 5)S y (0, 3)S
Para S se tiene tB − tA = 5 mientras que para S se
cumple tB − tA = 3
Curiosidad: observemos que el intervalo espacio-temporal
es invariante

31. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Tres formas de responder: la tercera
Transformaciones de Lorentz para Apolo (sistema S) y
Diana (sistema S’) nos dan lo siguiente:
El suceso A tiene coordenadas (0, 0)S y (0, 0)S
El suceso B tiene coordenadas (4, 5)S y (0, 3)S
Para S se tiene tB − tA = 5 mientras que para S se
cumple tB − tA = 3
Curiosidad: observemos que el intervalo espacio-temporal
es invariante

32. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Otra perspectiva
El suceso B (Diana llega a la estrella) tiene
S-coordenadas (4, 5) y es por esto por lo que Apolo
observa que Diana tarda 5 años en llegar
La pregunta es...
Cuando Diana llega a la estrella y han pasado tres años
en su reloj... ¿qué tiempo observa ella que ha transcurrido
para Apolo?
Por simetría, como Apolo observa las medidas temporales
de Diana dilatadas, entonces Diana verá las de Apolo
también dilatadas. ES DECIR, LOS TRES AÑOS QUE
OBSERVA DIANA EN SU RELOJ SE
CORRESPONDERÁN CON UN TIEMPO MÁS PEQUEÑO
EN EL RELOJ DE APOLO

33. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Otra perspectiva
El suceso B (Diana llega a la estrella) tiene
S-coordenadas (4, 5) y es por esto por lo que Apolo
observa que Diana tarda 5 años en llegar
La pregunta es...
Cuando Diana llega a la estrella y han pasado tres años
en su reloj... ¿qué tiempo observa ella que ha transcurrido
para Apolo?
Por simetría, como Apolo observa las medidas temporales
de Diana dilatadas, entonces Diana verá las de Apolo
también dilatadas. ES DECIR, LOS TRES AÑOS QUE
OBSERVA DIANA EN SU RELOJ SE
CORRESPONDERÁN CON UN TIEMPO MÁS PEQUEÑO
EN EL RELOJ DE APOLO

34. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Otra perspectiva
El suceso B (Diana llega a la estrella) tiene
S-coordenadas (4, 5) y es por esto por lo que Apolo
observa que Diana tarda 5 años en llegar
La pregunta es...
Cuando Diana llega a la estrella y han pasado tres años
en su reloj... ¿qué tiempo observa ella que ha transcurrido
para Apolo?
Por simetría, como Apolo observa las medidas temporales
de Diana dilatadas, entonces Diana verá las de Apolo
también dilatadas. ES DECIR, LOS TRES AÑOS QUE
OBSERVA DIANA EN SU RELOJ SE
CORRESPONDERÁN CON UN TIEMPO MÁS PEQUEÑO
EN EL RELOJ DE APOLO

35. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Otra perspectiva
El suceso B (Diana llega a la estrella) tiene
S-coordenadas (4, 5) y es por esto por lo que Apolo
observa que Diana tarda 5 años en llegar
La pregunta es...
Cuando Diana llega a la estrella y han pasado tres años
en su reloj... ¿qué tiempo observa ella que ha transcurrido
para Apolo?
Por simetría, como Apolo observa las medidas temporales
de Diana dilatadas, entonces Diana verá las de Apolo
también dilatadas. ES DECIR, LOS TRES AÑOS QUE
OBSERVA DIANA EN SU RELOJ SE
CORRESPONDERÁN CON UN TIEMPO MÁS PEQUEÑO
EN EL RELOJ DE APOLO

36. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
¿Cuánto más pequeño?
Simplemente, es el valor t0 dado por
t0
=3
1 − β2
por lo que t0 = 3 × 0, 6 = 1, 8 años
Esto es, cuando Diana llega a la estrella, ELLA OBSERVA
QUE EN LA TIERRA HAN TRANSCURRIDO
ÚNICAMENTE 1,8 años
Es lo natural... debemos esperar simetría (si cuando1
Apolo observa 5, Diana ha vivido 3, entonces cuando2
Diana observa 3, Apolo ha vivido 1,8)
1
Apolo–simultáneos
2
Diana–simultáneos

37. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
¿Cuánto más pequeño?
Simplemente, es el valor t0 dado por
t0
=3
1 − β2
por lo que t0 = 3 × 0, 6 = 1, 8 años
Esto es, cuando Diana llega a la estrella, ELLA OBSERVA
QUE EN LA TIERRA HAN TRANSCURRIDO
ÚNICAMENTE 1,8 años
Es lo natural... debemos esperar simetría (si cuando1
Apolo observa 5, Diana ha vivido 3, entonces cuando2
Diana observa 3, Apolo ha vivido 1,8)
1
Apolo–simultáneos
2
Diana–simultáneos

38. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
¿Cuánto más pequeño?
Simplemente, es el valor t0 dado por
t0
=3
1 − β2
por lo que t0 = 3 × 0, 6 = 1, 8 años
Esto es, cuando Diana llega a la estrella, ELLA OBSERVA
QUE EN LA TIERRA HAN TRANSCURRIDO
ÚNICAMENTE 1,8 años
Es lo natural... debemos esperar simetría (si cuando1
Apolo observa 5, Diana ha vivido 3, entonces cuando2
Diana observa 3, Apolo ha vivido 1,8)
1
Apolo–simultáneos
2
Diana–simultáneos

39. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
En el viaje de regreso...
Según Apolo (resp. Diana) la velocidad β (resp. −β) pasa
a ser −β (resp. β) pero como en las fórmulas está al
cuadrado nada debe variar...
Por tanto, cuando Apolo y Diana vuelven a encontrarse
(suceso C) tienen las siguientes versiones (como los
políticos y los medios):
Según Apolo, para él han pasado 10 años y para Diana 6:
ELLA ES CUATRO AÑOS MÁS JOVEN
Según Diana, para ella han pasado 6 años y para Apolo
1, 8 + 1, 8 = 3, 6: ÉL ES 2,4 AÑOS MÁS JOVEN

40. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
En el viaje de regreso...
Según Apolo (resp. Diana) la velocidad β (resp. −β) pasa
a ser −β (resp. β) pero como en las fórmulas está al
cuadrado nada debe variar...
Por tanto, cuando Apolo y Diana vuelven a encontrarse
(suceso C) tienen las siguientes versiones (como los
políticos y los medios):
Según Apolo, para él han pasado 10 años y para Diana 6:
ELLA ES CUATRO AÑOS MÁS JOVEN
Según Diana, para ella han pasado 6 años y para Apolo
1, 8 + 1, 8 = 3, 6: ÉL ES 2,4 AÑOS MÁS JOVEN

41. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
En el viaje de regreso...
Según Apolo (resp. Diana) la velocidad β (resp. −β) pasa
a ser −β (resp. β) pero como en las fórmulas está al
cuadrado nada debe variar...
Por tanto, cuando Apolo y Diana vuelven a encontrarse
(suceso C) tienen las siguientes versiones (como los
políticos y los medios):
Según Apolo, para él han pasado 10 años y para Diana 6:
ELLA ES CUATRO AÑOS MÁS JOVEN
Según Diana, para ella han pasado 6 años y para Apolo
1, 8 + 1, 8 = 3, 6: ÉL ES 2,4 AÑOS MÁS JOVEN

42. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
En el viaje de regreso...
Según Apolo (resp. Diana) la velocidad β (resp. −β) pasa
a ser −β (resp. β) pero como en las fórmulas está al
cuadrado nada debe variar...
Por tanto, cuando Apolo y Diana vuelven a encontrarse
(suceso C) tienen las siguientes versiones (como los
políticos y los medios):
Según Apolo, para él han pasado 10 años y para Diana 6:
ELLA ES CUATRO AÑOS MÁS JOVEN
Según Diana, para ella han pasado 6 años y para Apolo
1, 8 + 1, 8 = 3, 6: ÉL ES 2,4 AÑOS MÁS JOVEN

43. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
En otras palabras... ¿podemos distinguir entre los dos
sistemas de referencia?
¿Hay algo físico que le ocurre a Diana y no a Apolo o
viceversa?
Observemos que si el viaje fuera en un único sentido sí
habría SIMETRÍA
Pero la CLAVE está en el cambio de sentido...

44. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
En otras palabras... ¿podemos distinguir entre los dos
sistemas de referencia?
¿Hay algo físico que le ocurre a Diana y no a Apolo o
viceversa?
Observemos que si el viaje fuera en un único sentido sí
habría SIMETRÍA
Pero la CLAVE está en el cambio de sentido...

45. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
En otras palabras... ¿podemos distinguir entre los dos
sistemas de referencia?
¿Hay algo físico que le ocurre a Diana y no a Apolo o
viceversa?
Observemos que si el viaje fuera en un único sentido sí
habría SIMETRÍA
Pero la CLAVE está en el cambio de sentido...

46. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
En otras palabras... ¿podemos distinguir entre los dos
sistemas de referencia?
¿Hay algo físico que le ocurre a Diana y no a Apolo o
viceversa?
Observemos que si el viaje fuera en un único sentido sí
habría SIMETRÍA
Pero la CLAVE está en el cambio de sentido...

47. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
Es cierto que Apolo observa que Diana se va, luego da la
vuelta y regresa
También es cierto que Diana observa que Apolo (en la
Tierra) se aleja respecto de ella y que luego regresa...
Sin embargo, Diana experimenta cosas distintas a las que
experimenta Apolo
DIANA deja de ser un SISTEMA INERCIAL cuando tiene
que frenar para dar la vuelta y volver a acelerar... APOLO
SIEMPRE ES INERCIAL

48. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
Es cierto que Apolo observa que Diana se va, luego da la
vuelta y regresa
También es cierto que Diana observa que Apolo (en la
Tierra) se aleja respecto de ella y que luego regresa...
Sin embargo, Diana experimenta cosas distintas a las que
experimenta Apolo
DIANA deja de ser un SISTEMA INERCIAL cuando tiene
que frenar para dar la vuelta y volver a acelerar... APOLO
SIEMPRE ES INERCIAL

49. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
Es cierto que Apolo observa que Diana se va, luego da la
vuelta y regresa
También es cierto que Diana observa que Apolo (en la
Tierra) se aleja respecto de ella y que luego regresa...
Sin embargo, Diana experimenta cosas distintas a las que
experimenta Apolo
DIANA deja de ser un SISTEMA INERCIAL cuando tiene
que frenar para dar la vuelta y volver a acelerar... APOLO
SIEMPRE ES INERCIAL

50. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Situación simétrica... ¿sí o no?
Es cierto que Apolo observa que Diana se va, luego da la
vuelta y regresa
También es cierto que Diana observa que Apolo (en la
Tierra) se aleja respecto de ella y que luego regresa...
Sin embargo, Diana experimenta cosas distintas a las que
experimenta Apolo
DIANA deja de ser un SISTEMA INERCIAL cuando tiene
que frenar para dar la vuelta y volver a acelerar... APOLO
SIEMPRE ES INERCIAL

51. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
La bandeja de pasteles
Olvidé deciros que antes de partir, ambos acuerdan
regalarse unos pasteles a la vuelta...
Apolo se los coloca a su lado... ¡cómo huelen! Pero espera
el regreso de su hermana para regalárselos
Diana también los pone en el salpicadero de su nave... los
está viendo todo el tiempo...
Sin embargo, cuando vuelven a encontrarse, la única que
se come los pasteles es Diana porque los que ella llevaba
para Apolo están espachurrados

52. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
La bandeja de pasteles
Olvidé deciros que antes de partir, ambos acuerdan
regalarse unos pasteles a la vuelta...
Apolo se los coloca a su lado... ¡cómo huelen! Pero espera
el regreso de su hermana para regalárselos
Diana también los pone en el salpicadero de su nave... los
está viendo todo el tiempo...
Sin embargo, cuando vuelven a encontrarse, la única que
se come los pasteles es Diana porque los que ella llevaba
para Apolo están espachurrados

53. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
La bandeja de pasteles
Olvidé deciros que antes de partir, ambos acuerdan
regalarse unos pasteles a la vuelta...
Apolo se los coloca a su lado... ¡cómo huelen! Pero espera
el regreso de su hermana para regalárselos
Diana también los pone en el salpicadero de su nave... los
está viendo todo el tiempo...
Sin embargo, cuando vuelven a encontrarse, la única que
se come los pasteles es Diana porque los que ella llevaba
para Apolo están espachurrados

54. Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
La bandeja de pasteles
Olvidé deciros que antes de partir, ambos acuerdan
regalarse unos pasteles a la vuelta...
Apolo se los coloca a su lado... ¡cómo huelen! Pero espera
el regreso de su hermana para regalárselos
Diana también los pone en el salpicadero de su nave... los
está viendo todo el tiempo...
Sin embargo, cuando vuelven a encontrarse, la única que
se come los pasteles es Diana porque los que ella llevaba
para Apolo están espachurrados

55. de la paradoja
Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Un esquema espacio-temporal

56. El n´mero de felicitaciones por a˜o nuevo
u n
Hacia el espacio-tiempo tetradimensional Las matemáticas juegan... La paradoja de los gemelos
Ilustración de un efecto Doppler
Vemos que Diana recibe 10 felicitaciones. Diana recibe s´lo una antes de llegar a α Centauro, cuando hab´ pasado 3 a˜os, just
o ıan n
de dar la vuelta. Las 9 restantes le llegan durante su viaje de vuelta a raz´n de una cada 1/3 a˜o (4 meses).
o n