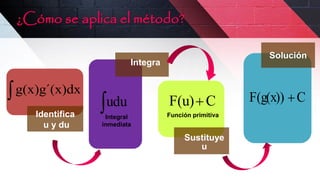
El documento explica el método de integración por cambio de variable, donde se sustituye el integrando o parte de él por otra función para facilitar la integración. Se detalla cómo identificar la nueva variable y su diferencial, y luego aplicar el cambio de variable para resolver la integral. Se proveen 4 ejemplos resueltos usando este método.

1. Método de integración por
cambio de variable
Dra. Ines Sanchez, Ing MsC Mgs

2. ¿En qué consiste el método de
sustitución o cambio de variable?
El método consiste en sustituir el integrando o parte de éste
por otra función para que la expresión resultante sea más fácil
de integrar.
Si escogemos un cambio de variable de modo que al aplicarlo
obtenemos en el integrando una función multiplicada por su
derivada, la integral en el integrando una función multiplicada
por su derivada, la integral será inmediata. Pero en ocasiones
un cambio mal escogido puede complicar más la integral.

3. Identifica
u y du
Integra
Solución
´(x)dx
g(x)g
du
u C
F(u)
Función primitiva
Sustituye
u
C
F(g(x))
¿Cómo se aplica el método?
Integral
inmediata

4. Integral 1
Si se quiere resolver esta integral aplicando alguna o algunas de
las fórmulas de integrales inmediatas, habría que resolver el
paréntesis multiplicando 10 veces el mismo integral para luego
multiplicar ese resultado por 6x. Este es un procedimiento muy
largo, lo recomendable es hacer una sustitución.

5. Cont. Integral 1
Cambio de variable:
Derivando:
Despejando:

6. 1
n
,
C
1
n
u
du
u
1
n
n
=
Aplicamos el cambio de variable, sustituyendo u y du:
Cont. Integral 1

7. Cont. Integral 1
Reemplazando u para regresar a la variable original, se
tiene el resultado de la integral:


8. Cambio de variable: Derivando:
Despejando para obtener el diferencial:
Integral 2

9. Cont. Integral 2
Simplificando:
Reemplazando u para regresar a la variable original, se
tiene el resultado de la integral:
Aplicamos el cambio de variable, sustituyendo u y du:
1
n
,
C
1
n
u
du
u
1
n
n


10. Integral 3
Cambio de variable: Derivando:
Despejando:
d[sen(u)] = u´cos(u)du

11. Cont. Integral 3
Simplificando:
Reemplazando u para regresar a la variable original:
Aplicamos el cambio de variable, sustituyendo u y du:
1
n
,
C
1
n
u
du
u
1
n
n


12. Cambio de variable:
Derivando x:
Despejando x para poder derivar:
2
u
1
du
arcsen(u)]
[
d
Integral 4

13. Cont. Integral 4
Usando la identidad trigonométrica , escribimos el
seno en función de la nueva variable:
1
(x)
cos
(x)
sen 2
2
Aplicamos el cambio de variable, sustituyendo u y du:

14. Simplificando:
Deshacemos el cambio:
Cont. Integral 4

15. Por tanto,

Cont. Integral 4

16. Bibliografía