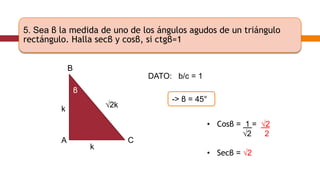
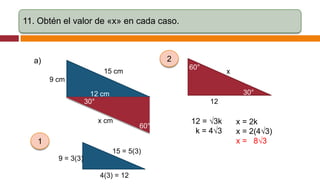
Este documento contiene un resumen de un taller de ejercicios de trigonometría. Incluye problemas que involucran hallar valores de funciones trigonométricas como secante, coseno y tangente dados ángulos en triángulos rectángulos y obtener el valor de la variable "x" en diferentes configuraciones trigonométricas.

1. TALLER DE
EJERCICIOS DE
TRIGONOMETRÍA
5° C
Alumnos: Nahela Pérez Vargas / Diego Rojas
Peña

2. 5. Sea β la medida de uno de los ángulos agudos de un triángulo
rectángulo. Halla secβ y cosβ, si ctgβ=1
B
DATO: b/c = 1
β
k
A
-> β = 45°
√2k
k
C
• Cosβ = 1 = √2
√2
2
• Secβ = √2

3. 4. En los siguientes ejercicios, hallar «x»
g) Sec(8x + 9) = Csc(7x + 6)
RRTT de ángulos
complementarios:
Sec β = Cos (90 – β)
8x + 9 + 7x + 6 = 90
15x +15 = 90
15x = 75
x = 5°
h)
Cos65° . Sec (x – 15) = 1
RRTT Inversas:
Cos β . Sec β = 1
65 = x – 15
x = 80°

4. 11. Obtén el valor de «x» en cada caso.
2
a)
60°
15 cm
x
9 cm
30°
12 cm
30°
12
x cm
60°
1
15 = 5(3)
9 = 3(3)
4(3) = 12
12 = √3k
k = 4√3
x = 2k
x = 2(4√3)
x = 8√3

5. B
b)
C
10√3
x
20
60°
A
H
30°
20
k √3
60°
k
10
20 = 2k
k = 10
D
k√3 = 10√3
x = 10√3