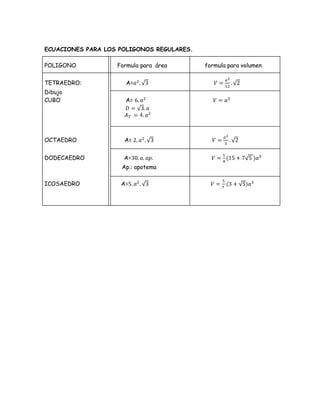
El documento describe los poliedros regulares, incluyendo sus características y fórmulas para calcular el área y volumen. Explica que un poliedro regular tiene caras polígonos regulares iguales y el mismo número de caras concurren en cada vértice. Solo hay cinco tipos de poliedros regulares: tetraedro, cubo, octaedro, dodecaedro e icosaedro. También proporciona fórmulas para calcular el área y volumen de cada poliedro regular.

1. Universidad de los llanos<br />Facultad de Ciencias Humanas y de la Educación<br />Programa de Lic. Matemáticas y Física<br />V Semestre<br />Desarrollado por: Julián Camilo Romero Díaz 141002113<br /> Ginneth Faisuly Vargas Daza 141002130<br />LOS POLIEDROS REGULARES<br />Áreas y Volúmenes.<br /> <br />¿Qué es un poliedro regular?<br />Un poliedro regular es aquel cuyas caras son polígonos regulares iguales y en cada uno de sus vértices concurren el mismo número de caras. <br />¿Cuántas clases de poliedros hay?<br />Sólo existen cinco tipos de poliedros regulares y son:<br />Tetraedro regular: 4 caras triangulares, que concurren tres en cada vértice. Tiene 4 vértices y 6 aristas.<br />Cubo: 6 caras cuadradas, que concurren tres en cada vértice. Tiene 8 vértices y 12 aristas.<br />Octaedro: 8 caras triangulares, que concurren cuatro en cada vértice. Tiene 6 vértices y 12 aristas.<br />Dodecaedro: 12 caras pentagonales regulares, que concurren tres en cada vértice. Tiene 20 vértices y 30 aristas.<br />Icosaedro: 20 caras triangulares, que concurren cinco en cada vértice. Tiene 12 vértices y 30 aristas<br />ÁREA DE LOS POLIEDROS REGULARES<br />El área total de un poliedro se determina calculando el área de una cara y multiplicando por el número de caras.<br />VOLUMEN DE LOS POLIEDROS REGULARES<br />Todos los vértices de un poliedro regular equidistan de un punto interior llamado centro. Haciendo pasar planos por este punto y por todas las aristas, el poliedro queda descompuesto en tantas pirámides iguales como caras tiene. Para calcular el volumen de un poliedro será suficiente calcular el volumen de una de estas pirámides y multiplicar por el número de caras del poliedro.<br />El volumen de una pirámide es, siendo B el área de la base y \"
ap.\"
la distancia del centro del poliedro al centro de la cara, distancia que se llama apotema. Siendo N el número de caras, pero (área total del poliedro), y en consecuencia <br />FORMULAS DE AREAS Y VOLUMENES<br />Como se ha indicado un polígono es regular si tiene sus lados iguales y sus ángulos iguales.<br />En la figura se muestran los elementos más importantes de un polígono regular.Radio (r): segmento que une el centro con un vértice. Es el radio de la circunferencia circunscrita.Apotema (a): Segmento que une el centro con el punto medio de un lado.En un polígono regular de n lados:Angulo central =360/nAngulo interior = 180 - 360/nÁrea = Perímetro x Apotema /2; A = n· L · a /2 , ya que es el área de n triángulos de base L y altura a(L/2)2 + a2 = r2 por ser triangulo rectángulo L/2, r y a<br />ECUACIONES PARA LOS POLIGONOS REGULARES.<br />POLIGONO Formula para área formula para volumen<br />TETRAEDRO: A=a2.3 V=a312.2 <br />Dibujo<br />CUBO A= 6.a2 V=a3<br /> D=3.a<br /> AT =4.a2<br /> <br />OCTAEDRO A= 2.a2.3 V=a33.2 <br />DODECAEDRO A=30.a.ap. V=14(15+75 )a3<br /> Ap.: apotema<br />ICOSAEDRO A=5.a2.3 V=57 (3+5)a3 <br /> <br />TALLER<br />Explique con sus palabras que es un polígono regular<br />Elabore una historia o historieta donde explique las características de cada uno de los poliedros regulares.<br />Marque con un “x” la respuesta correcta a las siguientes preguntas:<br />Un poliedro regular:<br />Es un polígono cuyas caras son polígonos que terminan en cada vértice.<br />Es un polígono cuyas caras son polígonos irregulares que terminan en cada vértice.<br />Es aquel cuyas caras son polígonos regulares iguales y en cada uno de sus vértices concurren el mismo número de caras.<br />Es aquel cuyas caras son polígonos regulares desiguales y en cada una de sus caras concurren el mismo número de vértices.<br />Un tetraedro es aquel polígono que cumple las siguientes características:<br />Tiene 4 vértices y 6 aristas que concurren tres en vértices. Tiene 4 caras que concurren tres en cada vértice.<br />Tiene 3 vértices y 6 aristas que concurren tres vértices. Tiene 4 caras que concurren tres en cada vértice. <br />Tiene 4 caras triangulares, que concurren tres en cada vértice. Tiene 4 vértices y 6 aristas.<br />Tiene 6 caras triangulares, que concurren cuatro en cada vértice. Tiene 6 vértices y 12 aristas.<br />¿Que es la apotema?<br />Un vértice.<br />La mitad de la cara de un polígono plano<br />Un punto<br />Segmento que une el centro con el punto medio de un lado<br />4.1 Elabore en cartulina (opcional) o en cualquier otro recurso, el poliedro con las siguientes dimensiones: <br />4 cm<br />4.2 Halle el área y perímetro del cubo con las medidas dadas.<br />Halle el área y el volumen a cada poliedro regular:<br />A. C.<br /> <br />B. D.<br /> <br />Desarrollado por: Julián Camilo Romero Díaz 141002113<br /> Ginneth Faisuly Vargas Daza 141002130<br />