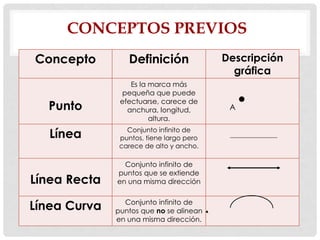
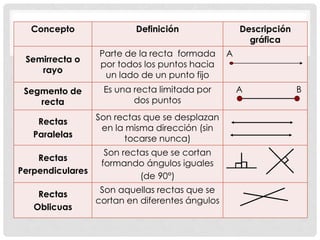
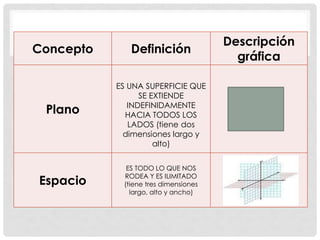
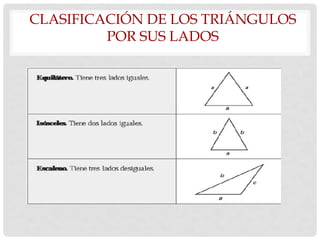
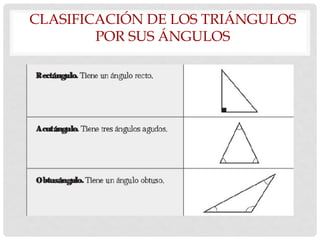
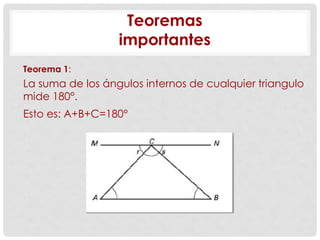
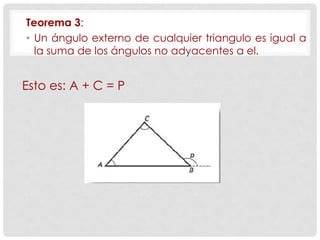
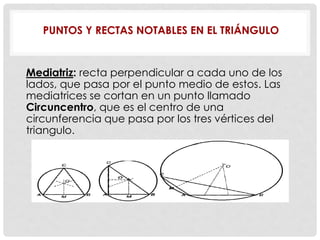
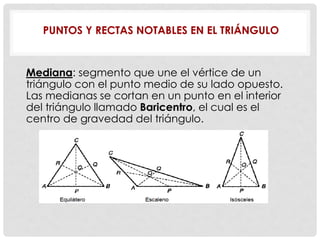
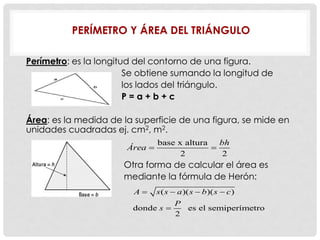
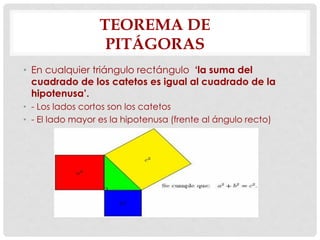
Este documento presenta conceptos básicos de geometría como puntos, líneas, planos, ángulos y su medición, clases de triángulos, teoremas sobre ángulos y triángulos, y fórmulas para calcular el perímetro y área de triángulos. También explica conceptos como congruencia, semejanza y el teorema de Pitágoras.

1. RA. 2.1 Resuelve problemas de
dimensiones lineales y superficiales de
figuras geométricas mediante
propiedades, teoremas, cálculos
aritméticos y algebraicos.
UNIDAD 2. Modelado angular,
lineal, de superficie y
espacial.

2. GEOMETRÍA
PARTE DE LA MATEMÁTICA DEDICADA AL ESTUDIO DE LAS
FORMAS Y PROPIEDADES DE LOS CUERPOS NATURALES. LA
PALABRA SE DERIVA DE LOS VOCABLOS GRIEGOS
GEO = TIERRA Y METRON = MEDIDA DE LA TIERRA.
• Geometría plana
- Se dedica al estudio de las
figuras planas.
• Geometría del espacio
- Estudia los cuerpos
geométricos sólidos, los cuales
tienen tres dimensiones: largo,
ancho y alto.

3. CONCEPTOS PREVIOS
Concepto Definición Descripción
gráfica
Punto
Es la marca más
pequeña que puede
efectuarse, carece de
anchura, longitud,
altura.
A
Línea Conjunto infinito de
puntos, tiene largo pero
carece de alto y ancho.
Línea Recta
Conjunto infinito de
puntos que se extiende
en una misma dirección
Línea Curva Conjunto infinito de
puntos que no se alinean
en una misma dirección.

4. Concepto Definición Descripción
gráfica
Semirrecta o
rayo
Parte de la recta formada
por todos los puntos hacia
un lado de un punto fijo
A
Segmento de
recta
Es una recta limitada por
dos puntos
A B
Rectas
Paralelas
Son rectas que se desplazan
en la misma dirección (sin
tocarse nunca)
Rectas
Perpendiculares
Son rectas que se cortan
formando ángulos iguales
(de 90°)
Rectas
Oblicuas
Son aquellas rectas que se
cortan en diferentes ángulos

5. Concepto Definición
Descripción
gráfica
Plano
ES UNA SUPERFICIE QUE
SE EXTIENDE
INDEFINIDAMENTE
HACIA TODOS LOS
LADOS (tiene dos
dimensiones largo y
alto)
Espacio
ES TODO LO QUE NOS
RODEA Y ES ILIMITADO
(tiene tres dimensiones
largo, alto y ancho)

6. ÁNGULOS
Llamamos ángulo a la abertura resultante de la
unión de dos semirrectas que tienen un mismo
punto de origen llamado vértice.
vértice
ángulo

7. NOTACIÓN Y SIMBOLOGÍA DE LOS
ÁNGULOS
Cualquier letra mayúscula situada en el
vértice fuera del ángulo hace referencia al
ángulo en cuestión. Por ejemplo < A
Se puede usar también un símbolo griego
dentro del ángulo, por ejemplo en el
ángulo α
Tres letras mayúsculas, cada una
refiriéndose a una semirrecta dejando la
letra de en medio definiendo al vértice en
cuestión. Por ejemplo < ABC
A
α
CB
A

8. SISTEMAS DE MEDICIÓN DE ÁNGULOS
SISTEMA Medida Unidades
SEXAGESIMAL
Consiste dividir una circunferencia en 360
partes iguales llamadas grados; el grado
se divide en 60 partes iguales llamadas
minutos y cada minuto se divide en 60
partes llamadas segundos.
Grado °
Minuto ‘
Segundo ‘’
Ej. 45° 23’ 55’’
DECIMAL
Consiste en expresar los ángulos en
grados sexagesimales y en fracciones
decimales de grados sexagesimales.
Ej. 38° 30' se expresa
como 38.5°, Porque 30'
equivalen 0.5 grados
CENTESIMAL
Consiste dividir una circunferencia en 400
partes iguales llamadas grados
centesimal; el grado se divide en 100
partes iguales llamadas minutos y cada
minuto se divide en 100 partes llamadas
segundos.
Grado g
Minuto m
Segundo s
Ej. 178g 89m28s
CIRCULAR
Los ángulos se miden en radianes; un
radián es el ángulo central de la
circunferencia, cuyo arco determinado
por los lados del ángulo tiene una longitud
igual al radio de la circunferencia.

9. EQUIVALENCIA ENTRE SISTEMAS DE
MEDICIÓN DE ÁNGULOS
 Como el perímetro del círculo está determinado por
P = 2 π r (2 por pi por radio), entonces una revolución
(vuelta) equivale a 2 π radianes.
 A su vez una revolución equivale a 360° y a 400g, por lo
tanto tenemos la siguiente equivalencia:
1 revolución = 360° = 2 π radian = 400g
1 rev = 360° = 400g = 6.2832 radian (con π = 3.1416)
Aplicando una regla de tres podemos pasar de un
sistema a otro
Por ejemplo 1 radian = 57.2957° = 0.1591 rev

10. Ángulo Medida Imagen
Ángulo agudo Mide menos de 90°
Ángulo recto Mide 90°
Ángulo obtuso Mide más de 90° y
menos de 180°
Ángulo llano Miden 180°
Ángulo cóncavo Miden más de180° y
menos de 360°
Ángulo perigonal Miden 360°
CLASIFICACIÓN DE ÁNGULOS
SEGÚN SU MEDIDA.

11. Nombre Definición Imagen
Ángulos opuestos por
el vértice.
Son los que resultan
cuando dos rectas se
cortan de manera que
se forman dos pares
de ángulos iguales.
Ángulos adyacentes.
Son los que están
formados de manera
que tienen un lado
común y los otros dos
pertenecen a la
misma recta .
CLASIFICACIÓN DE
ÁNGULOS POR SU POSICIÓN
b
d
ac
a = c y b = d
a
b

12. Nombre Suma de medidas Imagen
Complementarios
µ +Ø = 90°
Suplementarios
µ+Ø = 180°
Conjugados
µ+Ø = 360°
Ej.
CLASIFICACIÓN DE ÁNGULOS
POR LA SUMA DE SUS MEDIDAS
µ
Ø
µØ
µ
Ø

13. PARALELAS CORTADAS POR
UNA SECANTE
• Si se cortan dos rectas paralelas con una secante se forman 8
ángulos, que tienen las siguientes propiedades:
Nombre de
Ángulos
Ejemplo (figura) Características
Internos 3, 4, 5, 6
Externos 1, 2, 7, 8
Correspondientes
1 – 5 , 3 – 8
2 – 6 , 4 – 7
Iguales entre sí
Alternos internos 3 – 6 , 4 – 5 Iguales entre sí
Alternos externos 1 – 7 , 2 – 8 Iguales entre sí
Colaterales internos 3 – 5 , 4 - 6
Suplementarios
(suman 180°)
Colaterales externos 2 – 7 , 1 – 8
Suplementarios
(suman 180°)
Opuestos por el
vértice
1 – 4 , 2 – 3
5 – 7 , 6 - 8
Iguales entre sí

14. TRIÁNGULOS
Triangulo: figura geométrica localizada en un plano, formada
por tres rectas que se cortan en parejas y forman tres ángulos.
Un triángulo tiene:
- Tres lados (a, b c)
- Tres vértices (A, B, C)
- Tres ángulos ( <A, < B , <C)

15. CLASIFICACIÓN DE LOS TRIÁNGULOS
POR SUS LADOS

16. CLASIFICACIÓN DE LOS TRIÁNGULOS
POR SUS ÁNGULOS

17. Teoremas
importantes
Teorema 1:
La suma de los ángulos internos de cualquier triangulo
mide 180°.
Esto es: A+B+C=180°

18. Teorema 2:
La suma de los tres ángulos externos de cualquier
triangulo es igual a 360°.
• Esto es: p + q + r =360°.

19. Teorema 3:
• Un ángulo externo de cualquier triangulo es igual a
la suma de los ángulos no adyacentes a el.
Esto es: A + C = P

20. PUNTOS Y RECTAS NOTABLES EN EL TRIÁNGULO
Bisectriz: recta que divide a un ángulo en dos
partes exactamente iguales. Las bisectrices se
cortan en un punto interior del triángulo llamado
Incentro, el cual es el centro de un circulo inscrito
en el triángulo.

21. PUNTOS Y RECTAS NOTABLES EN EL TRIÁNGULO
Mediatriz: recta perpendicular a cada uno de los
lados, que pasa por el punto medio de estos. Las
mediatrices se cortan en un punto llamado
Circuncentro, que es el centro de una
circunferencia que pasa por los tres vértices del
triangulo.

22. PUNTOS Y RECTAS NOTABLES EN EL TRIÁNGULO
Mediana: segmento que une el vértice de un
triángulo con el punto medio de su lado opuesto.
Las medianas se cortan en un punto en el interior
del triángulo llamado Baricentro, el cual es el
centro de gravedad del triángulo.

23. PUNTOS Y RECTAS NOTABLES EN EL TRIÁNGULO
Altura: recta que pasa por un vértice y es
perpendicular al lado opuesto o la prolongación
de este. Las alturas se cortan en un punto llamado
Ortocentro.

24. PERÍMETRO Y ÁREA DEL TRIÁNGULO
Perímetro: es la longitud del contorno de una figura.
Se obtiene sumando la longitud de
los lados del triángulo.
P = a + b + c
Área: es la medida de la superficie de una figura, se mide en
unidades cuadradas ej. cm2, m2.
Otra forma de calcular el área es
mediante la fórmula de Herón:
( )( )( )
donde es el semiperímetro
2
A s s a s b s c
P
s
   

base x altura
2 2
bh
Área  

25. CONGRUENCIA
• Dos figuras son congruentes si al colocar una sobre la otra
todos sus puntos coinciden, es decir si tienen la misma forma y
tamaño, se representa con el símbolo .

26. CONGRUENCIA DE TRIÁNGULOS

27. SEMEJANZA DE FIGURAS
• Se dice que dos figuras son semejantes cuando
tienen la misma forma pero diferente tamaño.

28. SEMEJANZA DE TRIÁNGULOS
• Dos triángulos son semejantes cuando tienen sus
respectivos ángulos son iguales y sus lados son
proporcionales.

29. TEOREMA DE
PITÁGORAS
• En cualquier triángulo rectángulo ‘la suma del
cuadrado de los catetos es igual al cuadrado de la
hipotenusa’.
• - Los lados cortos son los catetos
• - El lado mayor es la hipotenusa (frente al ángulo recto)