Este documento presenta cálculos y simulaciones de diferentes tipos de rectificadores. Inicialmente analiza un rectificador monofásico resistivo, calculando la corriente media, eficaz y potencia disipada. Luego estudia un rectificador trifásico de punto medio, variando parámetros como la amplitud de tensión y agregando una fuente de corriente. Finalmente, modela un rectificador pentafásico de punto medio balanceado, graficando la tensión en la carga. El objetivo es comparar las diferentes configuraciones y analizar el efecto de los par

1. PONTIFICIA UNIVERSIDAD CATÓLICA DE VALPARAÍSO – CHILE ESCUELA DE INGENIERÍA
ELÉCTRICA
TAREA1. ELECTRONICA DE POTENCIA IEE 444
Carlos Antonio Vergara Reyes
José Leopoldo Ramos Ojeda
TAREA1. RECTIFICADORES: MONOFASICO, TRIFASICO PUNTO MEDIO Y COMPLETA.
ABRIL DE 2017
AYUDANTE ALEJANDRO FERRADA

2. INTRODUCCION
A continuación se realizaran cálculos matemáticos y simulaciones en PSIM y/o Matlab para
rectificadoresmonofásicosconcarga resistiva, rectificadores trifásicos de punto medio con carga
RLE y finalmente rectificadorestrifásicos de puente completaconcarga resistivaycondensadoren
paralelo. Para el primer caso es importante destacar que este tipo de rectificadores no son
utilizados comúnmente, pero sirven como ejemplificación para el aprendizaje y cálculo de
rectificadores más complejos, siendo este el rectificador monofásico resistivo el más básico de
todos. Se mostraran formasde onda enla carga, se mostraran el procedimientode integrales para
calcular los valores medios y eficaces de corriente y voltaje en la carga.
Para el segundo caso se analizara un rectificador de punto medio pentafásico (rectificador de 5
pulsos),en los cuales se cortocircuitara la fuente Io para calcular VLRE y luego se agregara Io y se
abrirá D2 y D4. Se analizaranloscambiosde formade ondaen lacarga con losefectosde lafuente
de corriente constante y al abrir dos diodos.
Finalmente en el tercer caso se realizaran netamente simulaciones de matlab para obtener la
característica no lineal entre wRC y 𝑉𝑐𝑚𝑖𝑛/𝑉𝑙𝑙 𝑝 𝑘 y se realizara la simulación en PSIMdel circuito
mostrando los valores de corriente y voltaje en el capacitor; así como también como la variación
corriente enlosdiodosenfunciónde lacapacitancia. Cabe destacarque el rectificadortrifásico de
puente completaesel másutilizadode todosyaque losdiodostienenque soportarsolounavezla
tensióninversade lafuente, porlocual estos tienen menor costo. También se aprovecha al 100%
y sin sobrecargas del transformador la energía del primario y secundario al conectar esta
estructura.

3. EJERCICIO I
Rut a utilizar: 17.537.300-4
Las magnitudesautilizarson:
V (wt)=A*sin(x-
𝜋
2
) [V]
E= (1+5)*10+0+0*10e-1= 60[V]
f = 50 [Hz]
R = 10+6+0.3 = 16.3 [Ω]
𝑇𝑗 = 100 [◦C]
𝑇𝑎 = 25 [◦C]
Para el diodo:
Rf= (10 + 7)= 17[mΩ]
𝑉𝑇𝑂 = (6 +1) · 10e−1 = 0.7 [V]
𝑅 𝑡ℎ𝐽𝐶 = 2 + e · 10e−1 [◦C/W]
𝑅 𝑡ℎ𝐶𝐷 = (3 + 1) · 10e−1 = 0.4 [◦C/W]
PREGUNTA 1
Considere A= 200+f*10+h= 200+30+0= 230
a) Grafique la forma de onda de la corriente en un intervalo desde ωt = 0[rad] hasta ωt =
4π[rad].
El circuito descrito es el siguiente de la figura 1:
Figura 1. Rectificador monofásico resistivo

4. La forma de onda será graficada en PSIM, como sigue en la figura 2:
Figura2. Forma de onda de la corriente en la resistencia
b) Calcule la corriente media. Explique brevemente las integrales utilizadas.
Calculamos las intersecciones de las funciones involucradas en el gráfico de la figura 2, con un
periodo de T=2 π como sigue:
Ir= (230*sin(wt-
𝜋
2
)+60)/16.3= 14.1104*sin(wt-
𝜋
2
)+3.6810 [A] = 0, dando como solución los valores
de wt= {1.3069, 4.9763}.
1) Ir media =
1
2𝜋
*∫ 14.1104 ∗ sin (wt −
𝜋
2
) + 3.6810 dwt
4.9763
1.3069 = 6.4857 [A]
En la ecuación1 se calculóel valormediode lacorriente enlacarga, se utilizaronlosvaloresde wt
de intersecciones de la figura 2 para evaluar los limites donde existía función distinta de cero.
c) Calcule la corriente eficaz. Explique brevemente las integrales utilizadas.
2) Ir eficaz =√
1
2𝜋
∗ ∫ (14.1104 ∗ sin (wt −
𝜋
2
) + 3.6810)^2 dwt
4.9763
1.3069 = 9.4865 [A]
En la ecuación2 se utilizanlosmismosvaloresde intersecciones de la figura 2, se prosigue con el
cálculo por definición de valor eficaz.
d) Calcule la 𝑹𝒕𝒉𝑫𝑨 necesaria para mantener la temperatura de juntura indicada.
Para el cálculode 𝑅 𝑡ℎ𝐷𝐴 se tiene que lacorriente eficazy media en los diodos es la misma que en
la resistencia por estar el circuito en serie, ya obtenido los valores necesarios en a y b para el
cálculo de la potencia 𝑃𝐴𝑉 como sigue:
3) 𝑃𝐴𝑉 = 𝑉𝑇𝑂 ∗ 𝐼 𝑚𝑒𝑑𝐷1 + 𝑅 𝐹 ∗ 𝐼 𝑒𝑓𝑡𝑜𝑡𝑎𝑙𝐷1
2
= 0.7*6.4867+0.017*9.4865^2= 6.0699 [W]

5. 4) 𝑅 𝑡ℎ𝐷𝐴 =
𝑇𝑗 −𝑇𝐴
𝑃 𝐴𝑉
=
100−25
6.0699
= 12.3561 [◦C/W].
PREGUNTA 2
Considere A como variable, y 𝑅 𝑡ℎ𝐷𝐴 = (10 + 7)= 17[◦C/W]
a) Calcule lapotenciadisipadaporel diodoapartirde las temperaturasylosvaloresde resistencia
térmica del diodo.
5) 𝑅 𝑡ℎ𝐽𝐴 = 𝑅 𝑡ℎ𝐷𝐴 + 𝑅 𝑡ℎ𝐽𝐶 + 𝑅 𝑡ℎ𝐶𝐷 = 17 + 2.7 + 0.4 = 20.1[◦C/W]
6) 𝑃𝐴𝑉 =
𝑇𝑗 −𝑇𝐴
𝑅 𝑡ℎ𝐽𝐴
=
100−25
20.1
= 3.7313 [𝑊]
b) Calcule,mediante unprogramacomputacional,el valorde A necesarioparaque el diodo disipe
la potencia determinada en a). ¿Tiene solución? Muestre y explique brevemente el código
utilizado.
Se calculara el valor de A según el siguiente código de matlab:
1. - syms A t;
2. - Imed= 1/(2*pi*16.3)*int(-A*cos(t)+60,1.3069,4.9763);
3. - Ief= (1/16.3)*sqrt(1/(2*pi)*int((-A*cos(t)+60)^2,1.3069,4.9763));
4. -result= (solve(3.7313==Imed*0.7+0.017*Ief^2))
5. -eval(result)
6. -result4=vpa(result)
Explicación del código:
1. Se definen las variables, A es la amplitud y t es la variable de integración.
2. Se define la función Imed que describe el cálculo de la corriente media de una señal por
definición. Con los valores de resistencia de 16.3 [Ω], periodo 2π, 60 [V], y los límites de
integración wt= {1.3069, 4.9763}.
3. Se realiza el mismo paso que en 2 pero para el valor eficaz de corriente.
4. Se resuelve simultáneamente la ecuación de la línea 2 y 3 para ser reemplazadas en la
función solve de la fórmula de potencia 𝑃𝐴𝑉 en el diodo.
5. Se muestra el resultado.
6. Se muestra el resultado exacto.

6. El resultado final de la simulación da como sigue:
ans =
1.0e+03 *
0.1196
-1.0847
result4 =
119.64786266710912488000687592515
-1084.7055634563843858756505855316
Se elige el valor positivo de result4 el cual da un valor de amplitud A= 119.6479.
c) En caso de que tengasolución,simule el circuitoenPSIM,considerandolaamplitudA obtenida.
Adjunte laimagende laformade ondade la corriente,juntoasu valormedioyeficaz.Compruebe
que con tales valores se obtiene la potencia disipada que calculó en a). En caso de que no tenga
solución, explique qué está ocurriendo circuitalmente.
Figura3. Forma de onda de la corriente en la carga con A= 119.6479

7. Figura 4. Valor medio de la corriente en la carga
Figura 5. Valor eficaz de la corriente en la carga
Ahorase corrobora el valorde potenciaenel diodo calculado en a, con los datos de la simulación
de PSIM.
7) 𝑃𝐴𝑉 = 𝑉𝑇𝑂 ∗ 𝐼 𝑚𝑒𝑑𝐷1 + 𝑅 𝐹 ∗ 𝐼 𝑒𝑓𝑡𝑜𝑡𝑎𝑙𝐷1
2
= 0.7*4.4775+0.017*6.1788^2= 3.7832 [W], dando un
resultado casi igual al de la ecuación 6.
CONCLUSIONES DEL EJERCICIO I
 Se puede concluirque si se reduce lapotencia 𝑃𝐴𝑉 a la mitad, 𝑅 𝑡ℎ𝐷𝐴 aumentacasi al doble.
 Al disminuirlaamplitudde laseñal de voltaje ala mitad,lapotencia 𝑃𝐴𝑉 se redujo casi en
la mitad.
 A mayor corriente media mayor potencia 𝑃𝐴𝑉, y viceversa.

8. EJERCICIO II
Rut a utilizar: 17.055.322-5
Las magnitudesautilizarson:
Fuentes de tensión de N fases balanceadas, de amplitud: A = 200 + h · 10 + f = 223
E = (1 + 5) · 10 + 5= 65 [V ]
R = 10 + 3 · (5-1)= 22[Ω]
Io = (1 + 7)= 8[A]
f = 50[Hz]
PREGUNTA 1
Considere N = 3, deje el diodo1abiertoy cortocircuite lafuente de corriente,quedando el circuito
como sigue:
Figura 6. Circuito con D21 abierto y Io cortocircuitado.

9. a) Grafique la forma de onda de la tensión en la carga desde ωt = 0[rad] hasta ωt = 4π[rad].
Figura 6. Forma de onda del voltaje en la carga
b) Calcule el valormediode latensióngraficadaena). Corrobore el resultado simulando en PSIM,
muéstrela forma de onda en un intervalo de tres ciclos, junto con su valor medio.
8) VRE media =
1
2𝜋
*∫ 223 ∗ sin(wt − 240°)dwt + ∫ 65 dwt
2.39
0.7518 + ∫ 223 ∗
4.7124
2.39
0.7518
0
sin(wt− 120°)dwt+ ∫ 223 ∗ sin(wt − 240°)dwt
6.2832
4.7124 = 146.3269 [𝑉]
Figura 7. Forma de onda de voltaje en la carga para 3 ciclos

10. Figura 8. Valor medio VRE
c) Mantenga abierto el diodo 1, y agregue la fuente de corriente, repita lo hecho en a) y b) para
estanuevaconfiguración.Expliquebrevemente porqué cambiólaformade onda de la tensión en
la carga.
En la figura9 se observael efecto de Io sobre la carga; por lo tanto cambia la forma de onda de la
carga respecto de la figura 7, ya que la fuente Io obliga a conducir a las fuentes V2 y V3 en sus
respectivos semiciclos negativos.
Figura 9. Efecto de Io sobre la carga RE.
Para la ecuación 9 se calculara el nuevo valor medio de la tensión en la carga considerando el
efecto de Io en la carga.
9) VRE media =
1
2𝜋
*∫ 223 ∗ sin(wt − 240°)dwt + + ∫ 223 ∗ sin(wt − 120°)dwt +
3𝜋/2
𝜋/2
𝜋/2
0
∫ 223 ∗ sin(wt − 240°)dwt
2𝜋
3𝜋
2
= 122.9463 [𝑉]

11. PREGUNTA 2
Con N= 5 realice los siguientes cálculos:
a) Cortocircuite lafuente de corriente. Grafique la forma de onda de la tensión en la carga desde
ωt = 0[rad] hastaωt = 2π[rad]. Indique losángulosdonde se ubican los peaks y las intersecciones
de fases.
En la siguiente figura se muestra el rectificador pentafásico a implementar.
Figura 10. Circuito a implementar
A continuaciónenlafigura11 se muestrala formade onda de tensiónen la carga, para un circuito
rectificador pentafásico balanceado de punto medio de la figura 10. Las fases están desfasadas
cada 72 grados respectivamente.
Figura11. Tensiónenlacarga para rectificadorpentafásicode puntomediobalanceado, con carga
RE

12. b) Calcule el valormediode latensióngraficadaena). Corrobore el resultado simulando en PSIM,
muéstrela forma de onda en un intervalo de tres ciclos, junto con su valor medio.
Para calcularel valor mediode latensiónenlafigura11, solobasta con integrarun intervalode 54
a 126 grados por ser un circuito pentafásico balanceado.
10) VRE media =
5
2𝜋
*∫ 223 ∗ sin(wt)dwt = 208.6141 [V]
126°
54°
Cabe destacar que también se podría haber hecho una integral en los diversos tramos de la
funciónentre los ángulos, 0°, 54°, 126°,198°,270°,342°, 360°para las tensionesque se reflejan en
los respectivos intervalos.
Figura 12. Forma de onda de VRE para 3 ciclos, junto con su valor medio.
Mediante lasimulaciónde PSIMylo que se muestra en la figura 12, se obtiene un valor medio de
tensión en la carga de 208.6139 [V] muy similar al calculador teórico en ecuación 10.

13. c) Repitaloanterior,peroagregandolafuente de corriente ydejandoabiertoel diodo2 y el diodo
4.
Figura 13. Circuito de la figura 10, con D2 y D4 abiertos, incluido Io
En la figura 14 se simula el circuito de la figura 13, para wt desde cero hasta 360 grados. Se
muestran las intersecciones y peaks de las fases v1, v3 y v5 respectivamente.
Figura 14. Simulación en PSIMde la VRE de la figura 13

14. A continuaciónenlaecuación11 se calculara el valor medio de la tensión del circuito de la figura
13.
11) VRE media =
1
2𝜋
*∫ 223 ∗ sin(wt − 288°)dwt + ∫ 223 ∗ sin(wt)dwt + ∫ 223 ∗
306°
162°
162°
54°
54°
0
sin(wt− 144°)dwt+ ∫ 223 ∗ sin(wt− 288°)dwt
360°
306° = 176.7407 [𝑉]
El valorcalculadopara la tensiónmediaenlacarga enPSIMda como resultado 176.7405 [V],valor
similar al calculado teorico.
Figura 15. Calculo de la tensión del valor medio de la tensión del circuito de la figura 13. Valor
medio mostrado en PSIM.
CONCLUSIONES DEL EJERCICIO II
 Para circuitosrectificadoresde puntomediobalanceados de N fases, basta con encontrar
el intervalo de ángulos deseado y multiplicarlo por la cantidad N de fases en el periodo,
para calcular su valor medio rápidamente.
 Al agregar fuentes de corriente en la carga, estas obligan a conducir a las fuentes
respectivasensussemiciclosnegativos.Tambiénal agregarIose disminuye el valormedio
de tensión en la carga, ya que también se refleja una tensión en la fuente de corriente
continua.

15. EJERCICIO III
Rut a utilizar: 17.537.300-4
PREGUNTA 1
b) las magnitudesautilizarson:
A = 200+5*10+7 = 257
f = 50[Hz]
R = (10-1)*10^2+0*10 = 900[Ω]
C = 10+3*(3-1) = 16[μF]
Circuitoa simular:
En el circuitoanteriorobtenemoslassiguientesformasde ondade corriente yvoltaje enel
capacitor:

16. La corriente eficaz total obtenidadesdelasimulaciónes:
Donde Ief = 0.6801[A]
La corriente eficazenel capacitorsegúnlasimulaciónes:

17. Donde ic eficaz= 0,4863[A]
La corriente enlosdiodoses:
Para D1:

18. Para D2:
Para D3:

19. Para D4:
Para D5:

20. Para D6:
Para las corrientesenunamismagráfica:

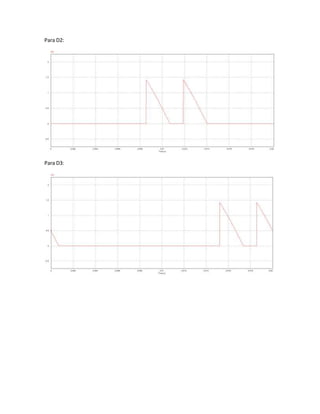
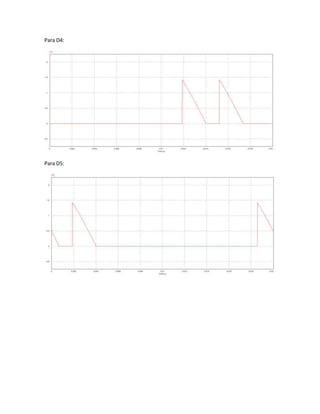
21. Si aumentamosel valorde C enun 50%, (C=24[μF]),obtenemos:
Si aumentamosel valorde C enun al doble (C=32[μF]),obtenemos:

22. Por ultimosi se aumentael valorde C al triple (C=48[μF])
CONCLUSIONES DEL EJERCICIO III
De losgráficosanterioresde observaque amedidaque aumentael valorde C(con todos los
demásparámetrosconstantes),tambiénaumentael valorpeakde lacorriente porlosdiodos.
BLIBLIOGRAFIA
 Apuntes Sr.DomingoRuizCaballero
 https://www.mathworks.com/help