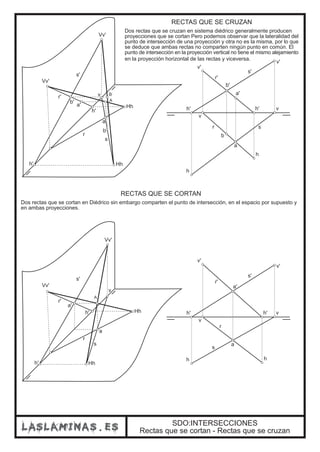
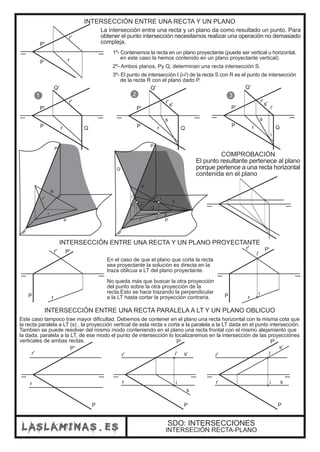
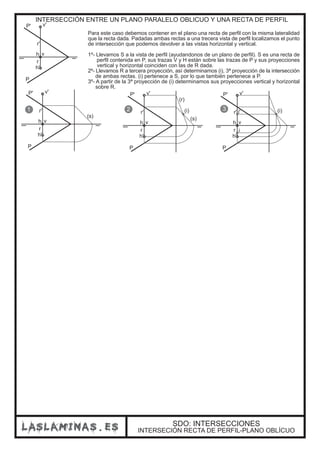
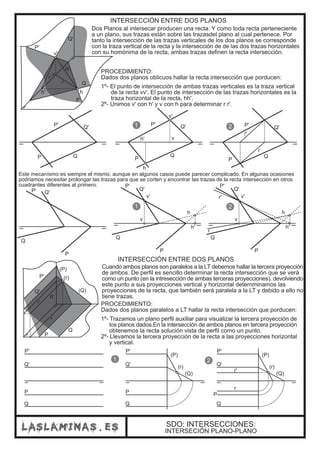
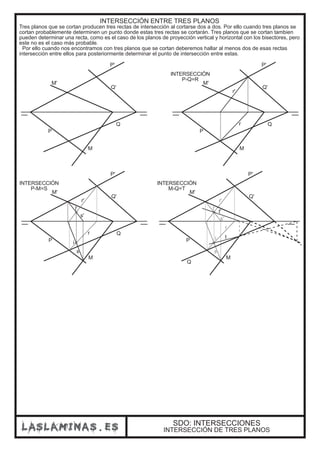
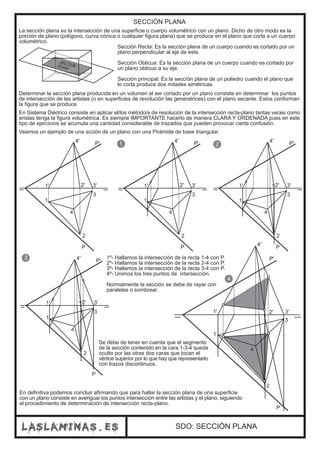
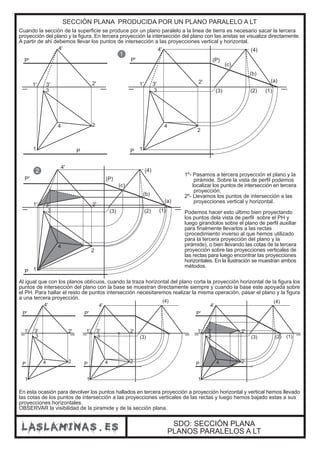
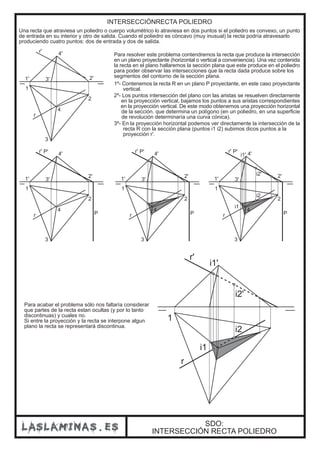
Este documento describe diferentes casos de intersección entre rectas y planos en el sistema diédrico. Explica que la intersección entre una recta y un plano da como resultado un punto, mientras que la intersección entre dos planos produce una recta. También cubre casos particulares como la intersección entre un plano proyectante y otro plano, o cuando las trazas de los planos no se cortan dentro de los límites del papel.