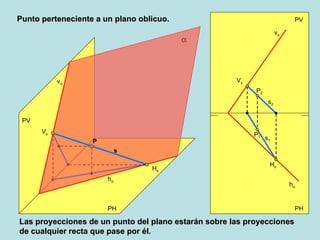
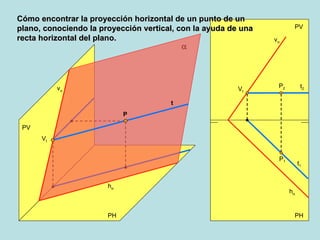
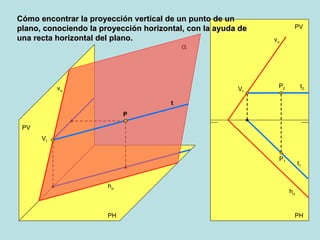
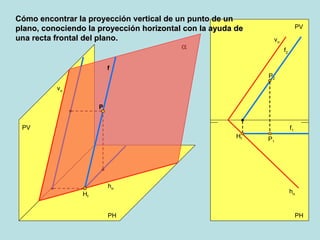
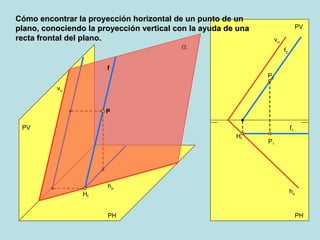
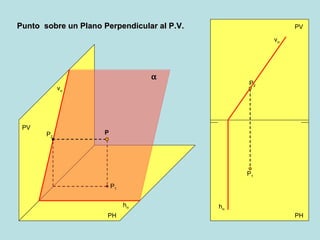
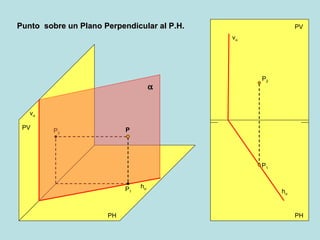
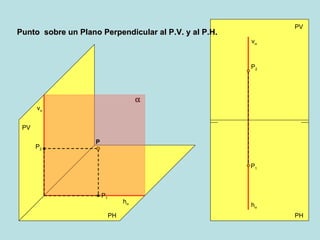
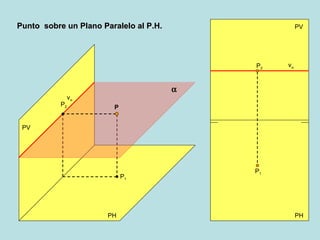
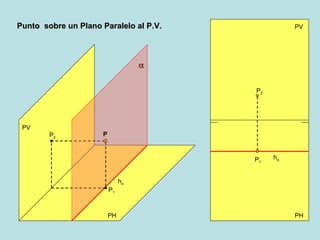
Este documento describe los diferentes métodos para encontrar las proyecciones de un punto en un plano oblicuo, dependiendo de la orientación del plano y la información disponible sobre el punto. Explica cómo calcular la proyección horizontal de un punto si se conoce la proyección vertical usando una línea horizontal de referencia, y viceversa, así como cómo hacerlo usando una línea frontal. También cubre puntos en planos perpendiculares o paralelos al plano vertical o horizontal.

1. SISTEMA DIÉDRICO El Punto en el Plano

2. Las proyecciones de un punto del plano estarán sobre las proyecciones de cualquier recta que pase por él. PV PH PH PV h  v   h  v  H s V s s H s V s s 2 s 1 P P 2 P 1 Punto perteneciente a un plano oblicuo.

3. Cómo encontrar la proyección horizontal de un punto de un plano, conociendo la proyección vertical, con la ayuda de una recta horizontal del plano. PV PH PH PV h  v   h  v  V t t V t t 2 t 1 P P 2 P 1

4. Cómo encontrar la proyección vertical de un punto de un plano, conociendo la proyección horizontal, con la ayuda de una recta horizontal del plano. PV PH PH PV h  v   h  v  V t t V t t 2 t 1 P P 2 P 1

5. PV PH PH PV h  v   h  v  H f f H f f 2 f 1 Cómo encontrar la proyección vertical de un punto de un plano, conociendo la proyección horizontal con la ayuda de una recta frontal del plano. P 2 P 1 P

6. PV PH PH PV h  v   h  v  H f f H f f 2 f 1 Cómo encontrar la proyección horizontal de un punto de un plano, conociendo la proyección vertical con la ayuda de una recta frontal del plano. P 2 P 1 P

7. Punto sobre un Plano Perpendicular al P.V. PV PH PH PV h  v  h  v  P 2 P 1 P 1 P 2 P 

8. PV PH PH PV h  v  P 2 h  v  P 2 P 1 P P 1  Punto sobre un Plano Perpendicular al P.H.

9. PV PH PH PV h  v   h  v  P 2 P P 1 P 2 P 1 Punto sobre un Plano Perpendicular al P.V. y al P.H.

10. PV PH PH PV v  v  P 2 P 2 P 1 P P 1  Punto sobre un Plano Paralelo al P.H.

11. PV PH PH PV h   h  P P 2 P 1 P 1 P 2 Punto sobre un Plano Paralelo al P.V.