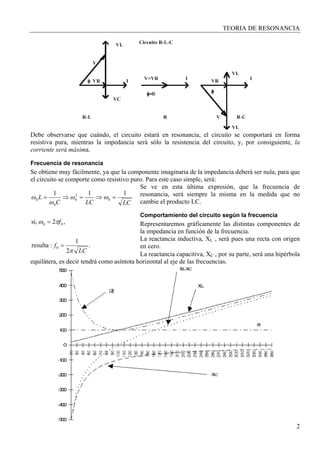
1) La teoría de resonancia describe el comportamiento de circuitos con elementos inductivos y capacitivos cuando la tensión y corriente están en fase. Esto ocurre a una frecuencia de resonancia específica. 2) En resonancia, el circuito se comporta como una resistencia pura y la impedancia es igual solo a la resistencia del circuito, logrando la corriente máxima. 3) La frecuencia de resonancia depende solo del producto LC y es la misma siempre que no cambien L o C.

1. TEORIA DE RESONANCIA
1
Teoría de Resonancia
Introducción
Definimos como resonancia al comportamiento de un circuito con elementos inductivos y capacitivos,
para el cual se verifica que la tensión aplicada en los terminales del mismo circuito, y la corriente
absorbida, están en fase. La resonancia puede aparecer en todo circuito que tenga elementos L y C.
Por lo tanto existirá una resonancia serie y otra resonancia paralelo o en una combinación de ambos.
El fenómeno de resonancia se manifiesta para una o varias frecuencias, dependiendo del circuito, pero
nunca para cualquier frecuencia. Es por ello que existe una fuerte dependencia del comportamiento
respecto de la frecuencia. Deviene de ello la gran importancia de los circuitos sintonizados,
especialmente en el campo de las comunicaciones, en lo que hace a la sintonización de señales de
frecuencias definidas o al "filtrado" de señales de frecuencias no deseadas.
Genéricamente se dice que un circuito está en resonancia cuando la tensión aplicada y la corriente están
en fase, el factor de potencia resulta unitario.
Resonancia serie
Para un circuito serie como el dibujado, la impedancia será la siguiente:
Si trazamos el diagrama de tensiones y corrientes del circuito, se verificará que la tensión adelantará,
Atrasará o estará en fase con la corriente. Esto resulta evidente de la expresión anterior, en la cual, para
algunas frecuencias se cumplirá que:
C
L
ω
ω
1
> ,
para otras frecuencias será:
C
L
ω
ω
1
< .
En el primer caso, se comporta el circuito en forma inductiva, en el segundo, en forma capacitiva y,
además, para alguna frecuencia, se cumplirá que:
C
L
ω
ω
1
= .
Para este caso, el circuito se encontrará en resonancia, ya que la impedancia será resistiva pura.(tensión
en fase con la corriente). Este tipo de circuito se denomina también Resonante en Tensiones, dado que
los módulos de las tensiones en los componentes reactivos, son iguales pero opuestos en fase y se
cancelan.
Los diagramas fasoriales son los que se dibujan a continuación:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−+=
1
11
1
C
LjRZ
ω
ω

2. TEORIA DE RESONANCIA
2
Debe observarse que cuándo, el circuito estará en resonancia, el circuito se comportará en forma
resistiva pura, mientras la impedancia será sólo la resistencia del circuito, y, por consiguiente, la
corriente será máxima.
Frecuencia de resonancia
Se obtiene muy fácilmente, ya que la componente imaginaria de la impedancia deberá ser nula, para que
el circuito se comporte como resistivo puro. Para este caso simple, será:
Se ve en esta última expresión, que la frecuencia de
resonancia, será siempre la misma en la medida que no
cambie el producto LC.
Comportamiento del circuito según la frecuencia
Representaremos gráficamente las distintas componentes de
la impedancia en función de la frecuencia.
La reactancia inductiva, XL , será pues una recta con origen
en cero.
La reactancia capacitiva, XC , por su parte, será una hipérbola
equilátera, es decir tendrá como asíntota horizontal al eje de las frecuencias.
.
2
1
:resulta
,2si,
111
0
00
0
2
0
0
0
LC
f
f
LCLCC
L
π
πω
ωω
ω
ω
=
=
=⇒=⇒=

3. TEORIA DE RESONANCIA
3
También hemos graficado en la figura, la componente imaginaria de la impedancia del circuito,
⎟
⎠
⎞
⎜
⎝
⎛
−
C
L
ω
ω
1
Finalmente representamos el módulo de la impedancia, es decir:
22
XRZ +=
Sobretensión y factor de selectividad / calidad
En los circuitos RLC serie, puede ocurrir que la tensión en los elementos reactivos sea mayor que la
tensión de alimentación. Este fenómeno se aprecia especialmente en frecuencias cercanas a la de
resonancia cuando la resistencia total es mucho menor que la reactancia del circuito.
En resonancia se cumple que:
LC VV =
tomemos pues para el análisis cualquiera de ellas.
R
V
IILVL == pero,ω
pues, en resonancia se cumple que el circuito se comporta en forma resistiva pura, es decir:
R=Z .
Por lo tanto, reemplazando, resulta:
V
R
L
VL
0ω
=
donde llamaremos a:
R
X
R
L
V
V
Q LL
=== 0
0
ω
factor de selectividad o simplemente Q del circuito.
Mediante un desarrollo análogo se llega, para el capacitor a:
R
X
CR
Q C
==
0
0
1
ω
Cualquiera sea la forma de calcular el Q, en resonancia el valor será idéntico, ya que XL = XC, para
ω = ω0. El factor de mérito, nos indica cuánto más grande es el valor de la reactancia que el de la
resistencia. Es conveniente que los circuitos resonantes, en general, tengan un Q elevado, pues su
comportamiento será mucho más dependiente de la frecuencia en la vecindad de la resonancia. Esto
sucederá cuando la resistencia sea pequeña.
Los circuitos prácticos usados en sintonía en el campo de las radio frecuencias (RF), tienen valores de
Q superiores a 100 en la mayoría de los casos. El factor Q se suele llamar también factor de
sobretensión o también factor de calidad.
Más adelante daremos una definición del Q basada en conceptos energéticos.
Admitancia [Y] cerca de la resonancia
Prácticamente, la información más útil sobre el comportamiento del circuito a frecuencias cercanas a la
de resonancia, se encuentra en la parte inferior (en forma de "V"), de la curva de la impedancia en
función de la frecuencia. Por lo tanto, resulta útil representar la función inversa, es decir La admitancia.
Z
Y
1
=

4. TEORIA DE RESONANCIA
4
Además esta curva tendrá la misma forma que la de la corriente, si excitamos al circuito con tensión
constante, ya que:
YVI =
También, la parte más importante se encuentra dentro de un intervalo comprendido en ±10 % f0, donde
f0 es la frecuencia de resonancia, ya que a frecuencias mayores, las variaciones son muy pequeñas.
Por último, conviene explicar también que en la gráfica se toma la frecuencia en coordenadas
logarítmicas, lo cual es muy común cuando se grafican funciones de la frecuencia, ya que el espectro de
los valores es muy amplio. Además aquí se tiene la ventaja adicional que el uso de coordenadas
logarítmicas simetriza la curva respecto de la frecuencia de resonancia. En las figuras siguientes,
observamos las curvas correspondientes al módulo y a la fase de la admitancia en la vecindad de la
resonancia. Vemos en ellas que para frecuencias bajas, el comportamiento es capacitivo (fase 90°).
Luego, el comportamiento capacitivo persiste pero en forma menos intensa ( circuito RC ), hasta la
frecuencia de resonancia, donde el comportamiento es resistivo ( fase 0°). Luego, el comportamiento se
torna levemente inductivo, a medida que crece la frecuencia respecto de la resonancia (circuito RL),
hasta que a frecuencias muy altas se torna fuertemente inductivo , circuito inductivo puro (fase -90°)
Refiriéndonos ahora a la curva del módulo de la admitancia, se observa que a frecuencias muy bajas,
resulta que dicho módulo es muy bajo, ya que la reactancia capacitiva es muy alta. En resonancia, el
circuito presenta la impedancia mínima e igual a la resistencia, por lo que la admitancia será máxima e
igual a la conductancia
R
GYY
1
0 ===
Por último, para frecuencias muy superiores a la de resonancia, la admitancia reduce su módulo, ya que
la reactancia inductiva es muy alta, con lo cual la impedancia es también alta.
Es interesante observar que si el circuito tiene una resistencia muy pequeña, la admitancia en resonancia
tiende a infinito, lo mismo que la corriente. Si las pérdidas suben, sube R y, consecuentemente se
reduce el módulo de admitancia en resonancia, por lo que la curva se aplasta. Resumiendo, si el Q del
circuito es elevado, la curva es más aguda, mientras que si Q es reducido, la curva resulta menos aguda.
En lo que se refiere a la fase, la variación de la misma es mucho más rápida a valores de Q altos. Si el
factor de mérito tiende a infinito, la fase varía bruscamente, pasando de +90° a -90°. Todo esto pone de
manifiesto que a valores de Q elevados, el fenómeno de resonancia se hace mucho más notorio que a
valores bajos.

5. TEORIA DE RESONANCIA
5
Los gráficos anteriores son correspondientes al circuito dibujado y con sus valores. Veamos también
qué sucede si en el mismo circuito anterior, adoptamos una resistencia R1= 5 Ω, es decir 10 veces
menor que la ya usada.
Y con la fase, vemos que varía mucho más bruscamente como lo habíamos anticipado.

6. TEORIA DE RESONANCIA
6
Puntos de potencia mitad
Veamos qué sucede si la componente reactiva total es igual a la resistencia del circuito.
jRR
YR
C
L
C
LjR
Z
Y
±
=⇒=−
⎟
⎠
⎞
⎜
⎝
⎛
−+
==
11
si,
1
11
ω
ω
ω
ω
de manera que el módulo de la admitancia valdrá:
2
11
0
22
==
+
=
Y
Y
RR
Y
mientras que el ángulo de fase adoptará el sig. valor:
( ) 0
451 ±=±=⎟
⎠
⎞
⎜
⎝
⎛
±= arctg
R
R
arctgϕ
El doble signo, deviene por el hecho que tendremos el mismo valor para el comportamiento capacitivo
(frecuencias inferiores a la de resonancia) y para el comportamiento inductivo (frecuencias superiores
a la de resonancia).
La potencia disipada en el circuito será en resonancia:
RYURIP 2
0
22
00 ==
Para los puntos en los cuales la componente reactiva es idéntica a la resistencia del circuito, tendremos:
22
2
0
22
02
12
RYU
R
Y
UP =⎟
⎠
⎞
⎜
⎝
⎛
=
Vemos que la potencia vale la mitad que la correspondiente a resonancia, es decir
2
0
12
P
P =
De estas consideraciones deviene el nombre de puntos de potencia mitad.
El intervalo de frecuencias comprendido entre los puntos de potencia mitad, define lo que se conoce
como ancho de banda de 3 dB, o simplemente ancho de banda. Este último valor es muy importante, ya
que define la selectividad del circuito resonante, parámetro muy importante fundamentalmente en
Comunicaciones cuando se estudian los circuitos sintonizados, ya que , en gran parte, dependerá de la
selectividad, la calidad de la recepción. El concepto de ancho de banda de 3dB, surge el hecho que la
potencia en los puntos de potencia mitad, cae justamente 3dB, lo cual puede demostrarse muy
fácilmente, como sigue
( ) ( )dBdB
P
P
P
P
3
2
1
log10
2
1
0
12
0
12
−==⇒=
Gráficamente resulta

7. TEORIA DE RESONANCIA
7
A continuación observamos el diagrama de fase.
Vemos que el ancho de banda del circuito es:
BW = ∆f = f2 – f1 = 3,1 KHz – 2,7 KHz = 0,4 KHz
observándose que el circuito es bastante selectivo, ya que el ancho de banda es sólo de 400 Hz. Como
veremos en el párrafo siguiente, la selectividad está íntimamente relacionada con el valor del Q.
Relación entre el factor de selectividad en resonancia y el ancho de banda
Determinemos la frecuencia correspondiente a cada uno de los punto de potencia mitad. Para f = f1,
resulta :
0
1
011
11
1
2
1
1
2
11
2
1
1
2
1
1
1
=−+
⇒=−+⇒=−
⇒=
−
⇒=−
LCL
R
CRLCCRLC
R
C
LC
RL
C
ωω
ωωωω
ω
ω
ω
ω
Se trata pues de una ecuación de segundo grado con una incógnita, de muy fácil resolución mediante la
fórmula resolvente, es decir:
LCL
R
L
R 1
42 2
2
1 +±=ω
En forma análoga podemos determinar la frecuencia f = f2 , haciendo:

8. TEORIA DE RESONANCIA
8
LCL
R
L
R
R
C
L
1
42
1
2
2
2
2
2 +±=⇒=− ω
ω
ω
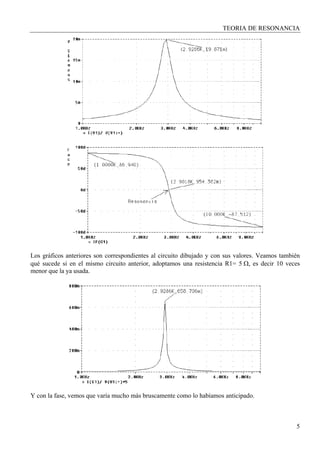
Por lo tanto, el ancho de banda en término de la pulsación, resulta:
BW
f
Q
ffBW
Q
R
L
L
RL
R
L
R
L
R
O
00
0
12
000
12
dondebanda;deAncho:BW
22
=
∆
=
−=
===
∆
⇒=+=−=∆
ω
ω
ωω
ω
ω
ωωω
Por lo tanto, podemos escribir:
BW
f
R
L
QO
00
==
ω
Aquí se observa que cuanto mayor es el factor de mérito del circuito, menor es el ancho de banda, con
lo que aumenta la selectividad.
Es interesante observar que la relación anterior provee un método sencillo para la medición del Q del
circuito, ya que bastará determinar la frecuencia de resonancia y las frecuencias para las cuales el
ángulo de fase vale ± 45°.
El concepto de selectividad define la mayor o menor aptitud que tiene un circuito para separar el resto
de las frecuencias respecto de la de resonancia.
Resonancia Paralelo
Para un circuito paralelo como el dibujado en la figura 1, demostraremos la equivalencia e identidad
con el circuito de la figura 2 y determinaremos luego la impedancia.
Para demostrar que ambos circuitos son idénticos y equivalentes, determinaremos la Admitancia [Y] de
la serie R1–L1y del paralelo RP–LP, de ambos circuitos. Las mismas deberán ser iguales.
(1)
1
11
1Circuito
22
1
22
1
1
22
1
1
1
1
1
1
1
1
11
1
1
1
1
1
L
L
LL
L
L
L
L
L
XR
X
J
XR
R
XR
jXR
Y
jXR
jXR
jXR
Y
jXRZ
Y
+
−
+
=
+
−
=
−
−
⋅
+
=
+
==
P
P
P
LPL
L
L
LP
LP
X
j
RXR
X
J
XR
R
X
j
R
Y
j
jjXRZ
Y
11
tendremos(2)y(1)Igualando(2).
11
1
:siendo;
111
2Circuito
22
1
22
1
1
1
1
1
−=
+
−
+
−=
−=+==
Dos números complejos son iguales si las partes Reales e Imaginarias resultan iguales. En efecto, los
circuitos serán iguales si:

9. TEORIA DE RESONANCIA
9
1
1
1
1
11
2
1
1
2
1
22
1
1
22
1
y
y
L
L
L
L
P
L
L
L
L
P
X
X
R
X
R
X
RR
X
XR
X
R
XR
R
P
P
+=+=
+
=
+
=
Considerando que generalmente:
ecuación.ladetérminootroalfrenteledespreciabvalordeserány:Entonces
.conductor)delOhmicaaResistencilaesquepresentetendrá(Se.10
1
1
2
1
1
11
L
L
X
R
R
RRX ⋅>
Luego tendremos que:
1
1
y
1
2
LL
L
P XX
R
X
R P
≅≅ o bien: LP = L1
Dadas estas condiciones ambos circuitos serán idénticos y equivalentes.
Frecuencia de Resonancia
Como en el circuito serie, en alguna frecuencia se dará que:
1
1
1
L
C
LP ω
ω
ω ==
En este caso por encontrarse ambos componentes en paralelo las corrientes por los mismos serán
iguales en módulo pero opuestas en fase. Resultando éste un circuito Resonante en Corrientes. El
diagrama fasorial se muestra en la próxima figura:
De la observación del mismo encontramos que, al cancelarse las corrientes reactivas
entre sí, la corriente por la resistencia RP es igual a la corriente de la fuente. Luego la
impedancia del circuito será:
Sobrecorriente y factor de selectividad / calidad
En los circuitos RLC paralelo, puede ocurrir que la corriente en los elementos
reactivos sea mayor que la corriente de alimentación. Este fenómeno se aprecia
especialmente en frecuencias cercanas a la de resonancia cuando la impedancia total
es mucho mayor que la reactancia de los componentes del circuito.
En resonancia, como lo hemos mencionado se cumple que:
LC II =
Luego el factor de selectividad o sobreintensidad será:
1
:entonces
LLP
L
P
P
L
RP
LCL
XQXQR
X
R
R
V
X
V
I
I
I
I
I
I
Q
P
P
P
⋅=⋅=
=====
1
2
0
1
R
X
R
R
I
V
I
V
Z
L
P
P
RP
≅
===

10. TEORIA DE RESONANCIA
10
Impedancia cerca de la resonancia
Esta curva tendrá la misma forma que la de tensión, si excitamos al circuito con corriente constante, ya
que:
ZIV =
Si adoptamos para el circuito de la figura 1, los siguientes valores:
R1 = 50 Ω; C1 = 150 nF y L1 = 20 mHy. I1 = 1 mA
Luego:
[ ] [ ] [ ]VARIV
XQR
R
X
Q
LfX
LC
f
P
LP
L
L
66,22665101
26653653,7
3,7
50
365
3651020290522
KHz2905
1015010202
1
2
1
3
1
3
0
93
0
=Ω⋅⋅=⋅=
Ω=⋅=⋅=
===
Ω=⋅⋅⋅=⋅⋅=
=
⋅⋅⋅
==
−
−
−−
ππ
ππ
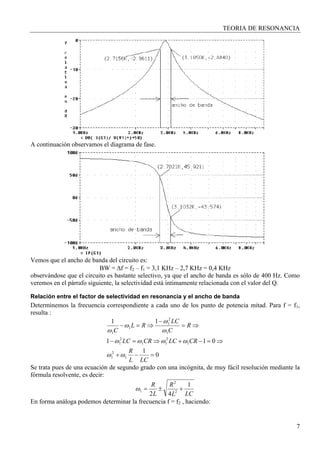
observamos las curvas correspondientes al módulo y a la fase de la impedancia en la vecindad de la
resonancia. Vemos en ellas que para frecuencias bajas, el comportamiento es inductivo (fase 90°. La
tensión adelanta a la corriente de línea o fuente). Luego, el comportamiento inductivo persiste pero en
forma menos intensa ( circuito RL ), hasta la frecuencia de resonancia, donde el comportamiento es
resistivo (fase 0°). Luego, el comportamiento se torna levemente capacitivo, a medida que crece la
frecuencia respecto de la resonancia (circuito RC), hasta que a frecuencias muy altas se torna
fuertemente capacitivo; circuito capacitivo puro (fase -90°. La tensión atrasa de respecto de la
corriente de la fuente)
Refiriéndonos ahora a la curva del módulo de la Impedancia, se observa que a frecuencias muy bajas,
resulta que dicho módulo es muy bajo, ya que la reactancia inductiva es muy baja y la capacitiva muy
alta. En resonancia, el circuito presenta la impedancia máxima e igual a la resistencia equivalente RP.
Por último, para frecuencias muy superiores a la de resonancia, la impedancia reduce su módulo, ya que
la reactancia inductiva es muy alta, pero la capacitiva será muy baja.
Si la resistencia propia del conductor resulta menor por ejemplo R1 = 5 Ω la impedancia del circuito en
resonancia crecerá en forma inversamente proporcional resultando RP = 26650 Ω. Este valor provoca un
cambio importante en la tensión dado que ahora valdrá:
[ ] [ ] [ ]VARIV P 65,2626650101 3
=Ω⋅⋅=⋅= −

11. TEORIA DE RESONANCIA
11
Este cambio ostensible de tensión provoca un importante crecimiento de las corrientes en los elementos
reactivos. Esta corriente circulará internamente, dentro del paralelo, motivo por el cual a este tipo de
circuito resonante se lo suele llamar Circuito Tanque.
La relación entre BW (ancho de banda) y el factor de selectividad (Q) para el circuito paralelo resulta
ser la misma que para el circuito serie.
BW
f
R
L
QO
0
1
10
==
ω
Aquí observamos que cuanto menor sea la resistencia del conductor que forma la bobina, mas selectivo
será el circuito.
Un caso general de resonancia paralelo
En el próximo circuito la admitancia entre los terminales 1-2, resulta:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
+
+⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
=
−
+
+
=+=
22222222
:tendremosmentealgebraicaOperando
;
11
LL
L
CC
C
CC
C
LL
L
CCLL
CL
XR
X
XR
X
j
XR
R
XR
R
Y
jXRjXR
YYY
El circuito se encontrará en resonancia cuando la admitancia resulte un
número real. Luego:
( )
C
LR
C
LR
LC
C
RLLR
C
XR
X
XR
X
C
L
CL
LL
L
CC
C
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+=+
+
=
+
2
2
0
22
0
2
0
22
0
2
0
2222
1
11
o.resolviendydoreemplazan;
ω
ω
ωω
ω
Cada uno de los cinco parámetros puede variar para obtener la resonancia. Además, las raíces deben ser
siempre un real positivo, luego habría resonancia cuando:
;a) 2222
C
LRy
C
LRó
C
LRy
C
LR CLCL 〈〈〉〉
de no cumplirse una u otra situación, resultará una pulsación imaginaria (raíces complejas), donde no
existirá valor de L ó C que satisfaga la condición de resonancia. Para una determinada frecuencia de la
fuente, puede obtenerse la condición de resonancia, variando:
CL RyRCL ;,
pero, al modificar uno de los parámetros para lograr el efecto de resonancia, ésta no se alcanzará para
cualquier valor de los restantes. Al variar L ó C y para determinadas relaciones de los restantes
parámetros, son posibles dos frecuencias donde se ha de cumplir la condición de resonancia, debido a
que se logra formar una ecuación de segundo grado para L y C.
Otros casos particulares serán:
LCC
LRR CL
1
;b) 0
22
=≠= ω y,
;
0
01
;c) 0
22
LCC
LRR CL === ω donde, el circuito podrá resonar a cualquier frecuencia.

12. TEORIA DE RESONANCIA
12
Proceso energético puesto en juego en la resonancia
a) En el caso de RL = RC = 0, la corriente “I” por el paralelo resulta cero, no hay transferencia de
energía al resto del circuito, solo se intercambia entre la bobina y el capacitor (intercambio entre
campo eléctrico y magnético).
b) Si alguna de las ramas tiene una componente resistiva distinta de cero, la corriente resultante
deja de ser cero (I > 0) y se transfiere energía al circuito. En el circuito paralelo la sumatoria de
energía puesta en juego por los campos magnéticos y eléctricos no es una constante. Existen
momentos en el que la fuente entrega energía al circuito y otros en los que los campos eléctricos
y magnéticos disipan su energía en las resistencias como efecto Joule (calor), no retornando
energía a la fuente dado que la corriente resultante iL está en fase con la tensión uC. El valor
instantáneo de la potencia “P” es siempre mayor que cero observándose además que el factor de
potencia fp = 1.
c) Si IC adelanta π/2 respecto de IL, la tensión UC estará en fase con IL de manera que la tensión en
el capacitor y la corriente de la bobina pasan por cero o máximo simultáneamente; las energías
de los campos están en fase, la energía en la bobina alcanzan el máximo y/o mínimo
simultáneamente no efectuándose intercambio de energía entre los campos. Al producirse el
efecto descrito, la fuente entrega energía almacenándose simultáneamente en la bobina y el
capacitor, luego y simultáneamente al bajar uC e iL, la energía se disipa en las resistencias. El
proceso descrito no se manifiesta cuando:
C
LRR CL == 22
Energía en un circuito resonante serie/paralelo

13. TEORIA DE RESONANCIA
13
En el cuadro de ecuaciones se demuestra que la energía puesta en juego es equivalente a la energía
máxima puesta en juego por la bobina o el capacitor.
El circuito resonante paralelo tiene
similitud al circuito serie, pero su
comportamiento es totalmente
opuesto al circuito paralelo; éste,
tiene alta impedancia en resonancia
mientras que el serie tiene alta
admitancia. Los diagramas aparentan
ser iguales pero las corrientes
reemplazan a las tensiones. Por
tanto, como se ha visto, la curva de
resonancia dibujada en admitancia
“Y” para el circuito serie, representa
la impedancia “Z” de resonancia en
paralelo. También resulta que la
energía almacenada permanece
constante.
Conclusión
La apropiada ubicación de los circuitos estudiados, además de la correcta elección de los componentes,
permitirá diseñar FILTROS y TRAMPAS para las frecuencias elegidas, canalizando las mismas por el
camino deseado aprovechando el concepto de selectividad anteriormente descrito; mejor será la
separación de cada una de las frecuencias, cuanto mayor sea el factor de selectividad adoptado.
Ing. Cocco Julio C.
Departamento de Ingeniería Eléctrica
UTN. FRRO
Enero de 2006
( )
( ) ( )
22
1
222222
2
0
2
2
22
222222
2
1
2
1
cos
2
1
cos
2
1
1
resonanciaPara;cos
1
2
1
:Luego;
cos
2
1
2
1
;
2
1
2
1
cos
2
;
CmmT
mmT
mT
m
Cm
CmCCmL
CmCmCm
CULIW
ttsenLItLtLsenIW
LC
t
C
tLsenIW
C
I
U
tCUCuWtsenLILiW
tUtsenUutsenIi
==
+=+=
=⎟
⎠
⎞
⎜
⎝
⎛
+=
=
====
−=−==
=
444 3444 21 ωωωω
ωω
ω
ω
ω
ωω
ωπωω