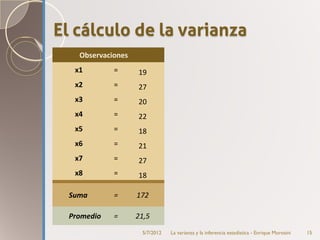
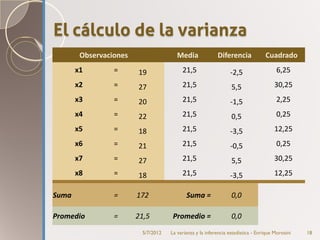
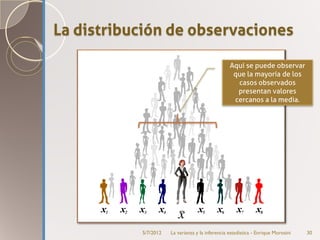
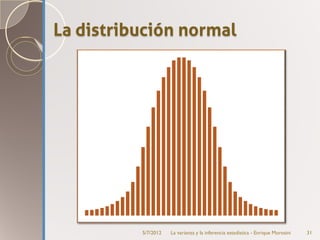
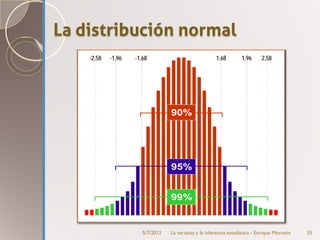
Este documento introduce el concepto de varianza y su uso en la estimación estadística. Explica que la varianza mide la variabilidad de un conjunto de datos y cómo se calcula. Luego describe cómo la varianza se puede descomponer en varianza explicada por factores conocidos y varianza error. Finalmente, discute la distribución normal de probabilidades y cómo esta se usa para realizar estimaciones estadísticas sobre parámetros poblacionales a partir de muestras.

1. El concepto de varianza
y su uso en la estimación estadística
Enrique Morosini
Universidad Nacional de Asunción
Facultad de Filosofía
Psicología Especialidad Clínica – Cátedra Psicometría Aplicada II
Asunción - 2012

2. Advertencia
 Este material intenta introducir los
principios lógico-conceptuales del
razonamiento estadístico relacionado con
la varianza y los procesos relacionados
con la estimación estadística.
 Las precisiones técnicas, los aspectos
críticos y los planteamientos estadísticos
estrictos deben ser consultados en la
bibliografía recomendada.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 2

3. La varianza
 Uno de los conceptos más importantes en
el análisis estadístico y el control
experimental de variables es la varianza.
 En principio, la varianza es una medida de
variabilidad que da cuenta del grado de
homogeneidad de un grupo de
observaciones, la fórmula de cálculo
es la siguiente:
N
2
∑ ( X i − µ X )2
i =1
σX =
N
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 3

4. APROXIMACIÓN
CONCEPTUAL
Y ESTADÍSTICA
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 4

5. Características colectivas
 Supongamos un grupo de personas que
comparten características comunes,
obviamente, observaremos también
características diferenciales.
 Supongamos, además, que estamos
realizando la tarea de cuantificar esas
respectivas características. Más o menos
podríamos representar la situación de la
siguiente manera:
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 5

6. Características individuales
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 6

7. Cuantificación de variables
 Denominemos estas variables evaluadas o
cuantificadas “X”, asignándole valores
según un sistema específico de
asignaciones.
 En la gráfica anterior el grupo de personas
se conformaría con asignaciones
diferentes de “X”, lo cual podríamos
representar de la siguiente manera:
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 7

8. Cuantificación de variables
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 8

9. Medidas “promedio”
 El conjunto de medidas podrían ser
resumidas mediante promedios o
medidas de tendencia central.
 En este caso utilizamos la media
aritmética (pudo haber sido la mediana o
la moda). Ese valor está representado por
un valor central y un “caso modelo” que
representaría las características promedio
del grupo:
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 9

10. La media como referencia
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 10

11. La dispersión de la media
 Una vez calculada la medida promedio
resulta fácil notar que existe una
diferencia (distancia) entre las medidas
individuales y el promedio.
 Cuanto mayor dispersión se observe
(distancia respecto a la media) menos
homogéneas son las observaciones.
 La dispersión puede cuantificarse
calculando la diferencia entre las medidas
individuales y el promedio.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 11

12. La distancia respecto a la media
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 12

13. El cálculo de la varianza
 La varianza como medida de dispersión es
el promedio de las diferencias cuadráticas
de las diferencias individuales respecto
de la media (tal como se anticipó).
 A partir de las observaciones registradas,
se aplica la siguiente fórmula:
n
2
∑(X i − X) 2
SX = i =1
n −1
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 13

14. El cálculo de la varianza
Observaciones
x1 = 19
x2 = 27
x3 = 20
x4 = 22
x5 = 18
x6 = 21
x7 = 27
x8 = 18
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 14

15. El cálculo de la varianza
Observaciones
x1 = 19
x2 = 27
x3 = 20
x4 = 22
x5 = 18
x6 = 21
x7 = 27
x8 = 18
Suma = 172
Promedio = 21,5
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 15

16. El cálculo de la varianza
Observaciones Media Diferencia
x1 = 19 21,5 -2,5
x2 = 27 21,5 5,5
x3 = 20 21,5 -1,5
x4 = 22 21,5 0,5
x5 = 18 21,5 -3,5
x6 = 21 21,5 -0,5
x7 = 27 21,5 5,5
x8 = 18 21,5 -3,5
Suma = 172
Promedio = 21,5
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 16

17. El cálculo de la varianza
Observaciones Media Diferencia
x1 = 19 21,5 -2,5
x2 = 27 21,5 5,5
x3 = 20 21,5 -1,5
x4 = 22 21,5 0,5
x5 = 18 21,5 -3,5
x6 = 21 21,5 -0,5
x7 = 27 21,5 5,5
x8 = 18 21,5 -3,5
Suma = 172 Suma = 0,0
Promedio = 21,5 Promedio = 0,0
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 17

18. El cálculo de la varianza
Observaciones Media Diferencia Cuadrado
x1 = 19 21,5 -2,5 6,25
x2 = 27 21,5 5,5 30,25
x3 = 20 21,5 -1,5 2,25
x4 = 22 21,5 0,5 0,25
x5 = 18 21,5 -3,5 12,25
x6 = 21 21,5 -0,5 0,25
x7 = 27 21,5 5,5 30,25
x8 = 18 21,5 -3,5 12,25
Suma = 172 Suma = 0,0
Promedio = 21,5 Promedio = 0,0
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 18

19. El cálculo de la varianza
Observaciones Media Diferencia Cuadrado
x1 = 19 21,5 -2,5 6,25
x2 = 27 21,5 5,5 30,25
x3 = 20 21,5 -1,5 2,25
x4 = 22 21,5 0,5 0,25
x5 = 18 21,5 -3,5 12,25
x6 = 21 21,5 -0,5 0,25
x7 = 27 21,5 5,5 30,25
x8 = 18 21,5 -3,5 12,25
Suma = 172 Suma = 0,0 94
Promedio = 21,5 Promedio = 0,0 13,43
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 19

20. COMPONENTES
DE LA VARIANZA
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 20

21. Varianza conocida
 Supongamos que el grupo de personas
representado anteriormente pertenecen a
un grupo dentro del cual comparten
características comunes. Entendemos que
estos aspectos comunes hacen que sean
más similares entre sí que con otras
personas en determinados aspectos.
 Teóricamente, si sus características
dependieran únicamente de ese factor
común las características deberían ser
iguales a la media.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 21

22. Varianza explicada
 Supongamos, además, que conocemos
otros factores que influyen en las
diferencias individuales: el sexo y la edad.
Dicho de otro modo, las puntuaciones
varían conforme fueran hombres o
mujeres, más jóvenes o mayores que la
edad promedio.
 Estas variables explican parte de las
variaciones o desviaciones de la media.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 22

23. Agregar símbolo de la media
Varianza explicada
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 23

24. Varianza error
 Aún conociendo estas variables
responsables de la variación, es posible
observar que las puntuaciones presentan
algunas variaciones respecto a los valores
medios o esperados.
 Este grado de variación se conoce como
varianza error.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 24

25. Varianza error
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 25

26. DISTRIBUCIÓN
DE PROBABILIDADES
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 26

27. Probabilidades
 Durante muchos años el azar y la
posibilidad de establecer suposiciones que
permitan comprender las leyes que le
subyacen fueron objeto de interés por
científicos y matemáticos.
 El concepto que ha permitido acercarse a
comprensión del azar es el estudio
sistemático de la manera en cómo se
distribuyen empíricamente los sucesos y el
análisis de las probabilidades de
ocurrencia de un fenómeno.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 27

28. Distribución de probabilidades
 La forma en cómo se distribuyen las
probabilidades de ocurrencia de un
determinado fenómeno ha generado
modelos que facilitan mecanismos de
estimación.
 Uno de estos modelos cuyo uso se ha
extendido (en forma peculiar en las
ciencias sociales, del comportamiento y la
salud) es el de la distribución normal, cuya
forma intuitiva se representa a
continuación:
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 28

29. La distribución de observaciones
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 29

30. La distribución de observaciones
Aquí se puede observar
que la mayoría de los
casos observados
presentan valores
cercanos a la media.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 30

31. La distribución normal
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 31

32. ESTIMACIÓN
ESTADÍSTICA
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 32

33. Aproximación conceptual
 El principio fundamental en el proceso de
estimación estadística es la necesidad de
conocer los parámetros de una población
a partir de las observaciones de valores
en una muestra.
 Un conjunto de datos obtenidos de una
muestra, utilizando el concepto de
varianza y la distribución de probabilidad,
representa un valor con cierta
probabilidad de representar el parámetro
de la población.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 33

34. Aproximación conceptual
 Si utilizamos el modelo de distribución
normal, que como lo habíamos adelantado
es uno de los más utilizados (atendiendo
que existen críticas importantes respecto a
esta suposición), es posible conocer de
antemano la distribución teórica de
probabilidades para una distribución
similar.
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 34

35. La distribución normal
-2,58 -1,96 -1,68 1,68 1,96 2,58
5/7/2012 La varianza y la inferencia estadística - Enrique Morosini 35

36. Error de estimación
 Las observaciones distribuidas conforme
al modelo de distribución normal,
presenta una dispersión cuya unidad de
medida es el error de estimación.
 Este error de estimación, cuya unidad de
medida es sigma (σ), se basa en el cálculo
de la raíz cuadrada de la varianza:
2
σ σx
σε
= = x
n n
5/7/2012 La varianza y la estimación estadística - Enrique Morosini 36

37. El proceso de estimación
 La estimación propiamente se realiza
aplicando un margen de error a la medida
muestral objeto de estimación (θ).
 El margen de error aplicado es el valor del
error de medición multiplicado por el
valor z correspondiente a la probabilidad
de ocurrencia del suceso, también
llamado confianza de estimación.
θ ± σ .z
5/7/2012 La varianza y la estimación estadística - Enrique Morosini 37