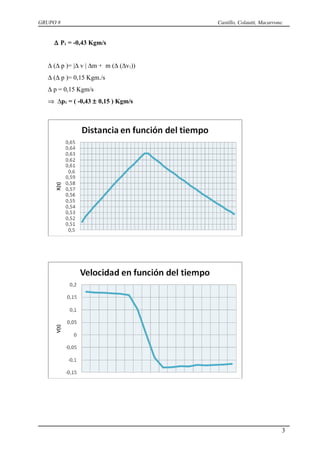
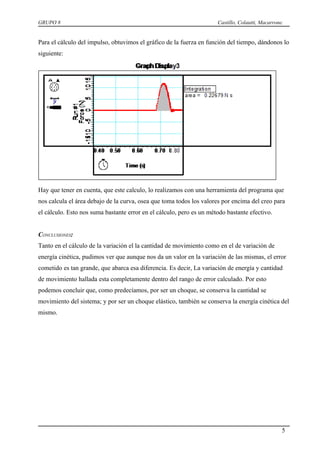
Este documento presenta los conceptos teóricos de cantidad de movimiento, energía cinética y mecánica para sistemas de partículas. Describe un experimento de colisión elástica entre dos carritos y los cálculos de variación de cantidad de movimiento y energía cinética para cada carrito y el sistema. Concluye que aunque hay errores en las mediciones, la variación de cantidad de movimiento y energía cinética calculadas están dentro del rango de error, por lo que se conservan en la colisión elástica como se predijo teóric

1. GRUPO 8 Castillo, Colautti, Macarrone.
INTRODUCCIÓN TEÓRICA.
CONSIDERACIONES TEÓRICAS.
◘ Cantidad de movimiento (partículas): Se define como la masa por la velocidad de esa
partícula p = m · v , definida en un instante t cualquiera.
◘ Cantidad de movimiento (Sistema de partículas): Se defina como ∑ mi · vi , o sea la
sumatoria de todas las cantidades de movimiento de todas las partículas presentes en el
sistema.
Condiciones necesarias para la conservación de p en una colisión para un sistema de
partículas.
Para se conserve p en una colisión, el po tiene que ser igual al pf, para esto planteamos 2
condiciones:
1) ∑ Fext = 0. Si no hay fuerzas externas aplicadas en los cuerpos, estos se mueven
libremente y luego del choque se mantiene la ptotal.
2) Si actúa una fuerza de rozamiento, y se toma en cuenta un instante muy pequeño antes y
después del choque, se puede despreciar la ∆p y se lo toma como ∆p = 0.
◘ Impulso: I = ∆p = m·Vf - m·Vi
El impulse se define como la variación de p, puede ser por una fuerza (cte) externa que
actuó sobre un cuerpo al cual la aceleró o viceversa y cambio su velocidad.
Manteniendo su masa y con una variación en la velocidad, se produce una variación de la
cantidad de movimiento.
I = ∆p = ∫tot F dt
F = dp / dt ⇒ ∫tot Fdt = ∫pop dp
si F = cte ⇒ I = ∆p = F· ∆t
◘ Energía cinética de un sistema de partículas
La variación de la energía cinética se define como ∆Ec = WTodas las fzas
Ec = ½ · m · v²
El trabajo de todas las fuerzas actuantes en el sistema definen la ∆Ec, si hubo alguna
modificación en las velocidades entre dos instantes, aquí se presentó la variación.
◘ Energía mecánica de un sistema de Partículas
La ∆Em se define como Em = Ec + Ep = W fzas no cons.
La Em es la E total del sistema presente. Para presentar la variación de la misma de
1

2. GRUPO 8 Castillo, Colautti, Macarrone.
toman en cuenta las fuerzas no conservativas ( internas y externas) del sistema, que son
las que producen, ya sea por un rozamiento o una fuerza externa, una variación de
energía, la cual se pierde en forma de calor.
◘ Colisiones:
- Plástica: Aquella en la que se conserva la cantidad de movimiento (esto sucede ⇔
∑Fzas ext = 0) y la variación de la Energía cinética es menor que 0 y máxima en módulo.
En este tipo de colisión las partículas quedan incrustadas y se siguen moviendo juntas.
- Elástica: Aquella en la que se conserva la cantidad de movimiento y también la Energía
cinética.
MATERIALES
• 2 Carritos (masas: (1505,5 ± 2)g y (1839,0 ± 2)g )
• Sensores de movimiento.
• Computadora.
• Balanza.
DESARROLLO Y RESULTADOS.
Choque elegido:
CHOQUE ELÁSTICO
(+)
1 2
• Móvil 1:
Masa Total = (1505,5 ± 2) g
V1 = Velocidad inicial del móvil 1 ≅ 0,17 m/s (dato sacado del gráfico, en un rango de
velocidades posibles marcado)
V1 f = Velocidad final del movil 1 (luego del choque) ≅ -0,12 m/s
∆v = corresponde a la mínima división en la escala del gráfico de velocidad en función del
tiempo.
⇒ ∆P1 = mt · ∆v1
∆P1 = 1,5055 Kg · (-0,12 m/s – (0,17 m/s))
2

3. GRUPO 8 Castillo, Colautti, Macarrone.
∆ P1 = -0,43 Kgm/s
∆ (∆ p )= |∆ v | ∆m + m (∆ (∆v1))
∆ (∆ p )= 0,15 Kgm./s
∆ p = 0,15 Kgm/s
⇒ ∆p1 = ( -0,43 ± 0,15 ) Kgm/s
3

4. GRUPO 8 Castillo, Colautti, Macarrone.
• Móvil 2:
Masa total = (1839,0 ± 2) g
V2= Velocidad inicial del móvil 2 ≅ -0,21 m/s ( La velocidad es negativa porque el sistema
de referencia que tomamos era positivo en el sentido del movimiento inicial del móvil 1)
V2f ≅ 0,15 m/s
⇒ ∆P2 = mt · ∆v2
P2 = 1,839 Kg · ( 0,15 m/s – (-0,21 m/s))
P2 = 0,66 Kgm/s
∆ (∆ p )= |∆ v | ∆m + m (∆ (∆v1))
∆ (∆ p )= 0,19 Kgm./s
∆ p = 0,19 Kgm/s
⇒ ∆p2 = ( 0,66 ± 0,19 ) Kgm/s
∆P SIST= ∆p1 + ∆p2 = -0,43 Kgm/s + 0,66 Kgm/s = 0,23 Kgm/s.
∆ (∆P SIST) = ∆ (∆p1) + ∆(∆p2) = (0,19 + 0,15) Kgm/s = 0,34 Kgm/s
⇒ ∆ P SIST = ( 0,23 ± 0,34 ) Kgm/s
• Masa del sistema final = ( 3344,5 ± 4) g
Ec (inicial) = ½ · 1,5055 kg · (0,17m/s)² + ½ · 1,839 kg · (-0,21m/s)²
Ec (inicial) = 0,06 J
Ec (final) = ½ · 1,5055 kg · ( -0,12 m/s)² + ½ · 1,839 kg · (0,15 m/s)²
Ec (final) = 0,03 J
∆ Ec = (0,03 – 0,06) J = -0,03 J
Este valor, es en parte producto del error cometido en las mediciones, y por otra parte es el
trabajo de la fuerza de rozamiento, que por más que sea mínima, va a influir a la hora del
experimento.
4

5. GRUPO 8 Castillo, Colautti, Macarrone.
Para el cálculo del impulso, obtuvimos el gráfico de la fuerza en función del tiempo, dándonos lo
siguiente:
Hay que tener en cuenta, que este calculo, lo realizamos con una herramienta del programa que
nos calcula el área debajo de la curva, osea que toma todos los valores por encima del creo para
el cálculo. Esto nos suma bastante error en el cálculo, pero es un método bastante efectivo.
CONCLUSIONES:
Tanto en el cálculo de la variación el la cantidad de movimiento como en el de variación de
energía cinética, pudimos ver que aunque nos da un valor en la variación de las mismas, el error
cometido es tan grande, que abarca esa diferencia. Es decir, La variación de energía y cantidad
de movimiento hallada esta completamente dentro del rango de error calculado. Por esto
podemos concluir que, como predecíamos, por ser un choque, se conserva la cantidad se
movimiento del sistema; y por ser un choque elástico, también se conserva la energía cinética del
mismo.
5