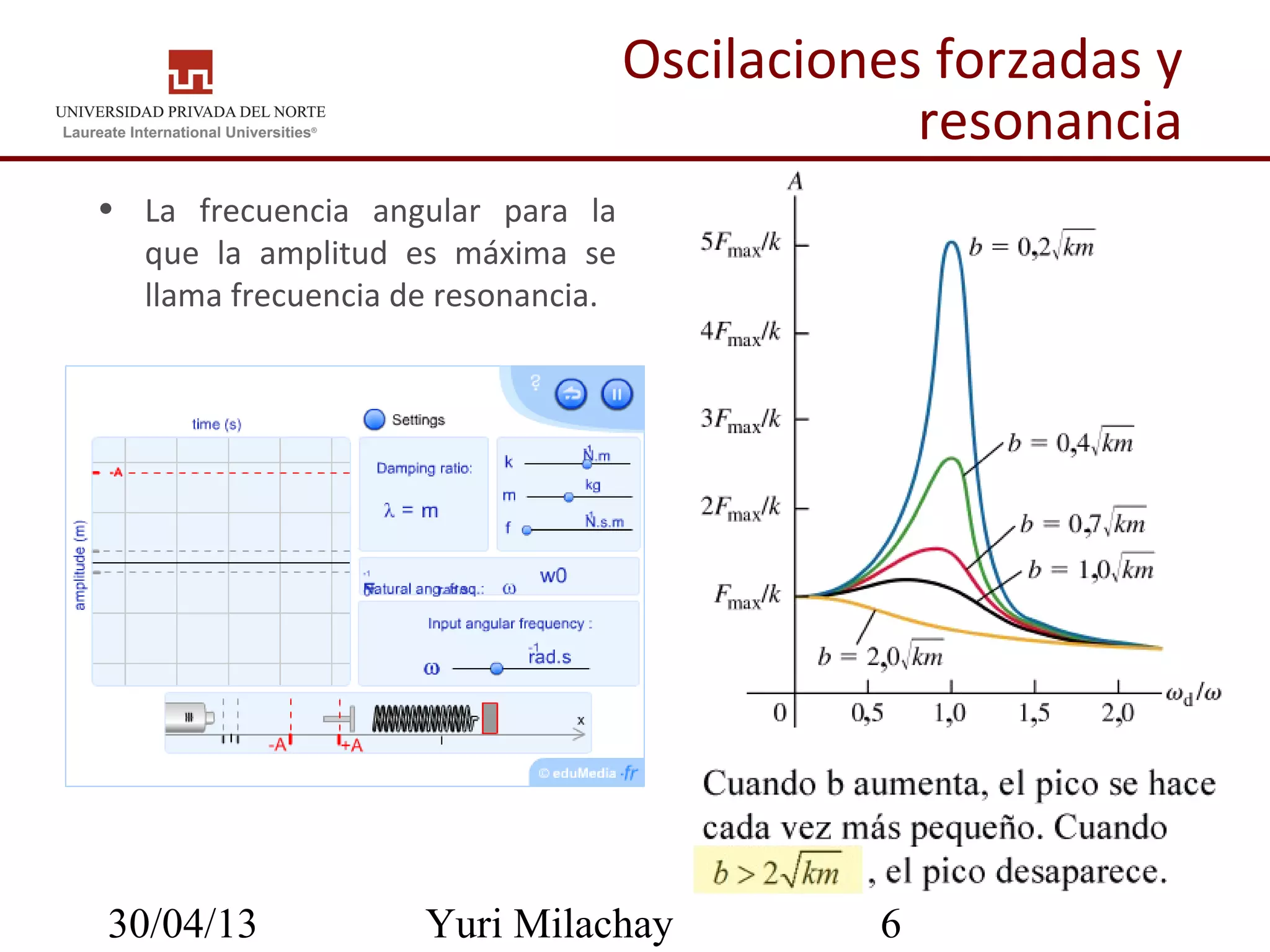
Este documento presenta una lección sobre oscilaciones forzadas y resonancia impartida por el Mg. Yuri Milachay. La lección incluye una introducción al tema, objetivos de aprendizaje, ecuaciones matemáticas que describen oscilaciones forzadas, y ejemplos y ejercicios para aplicar los conceptos.

1. CARRERADEINGENIERÍAINDUSTRIAL
FACULTADDEINGENIERÍAYARQUITECTURA
Física 2
Departamento de Ciencias
Mg. Yuri Milachay Vicente
Yuri.milachay@gmail.com
Semana 4
Oscilaciones forzadas y resonancia

2. 30/04/13 Yuri Milachay 2
¿Qué hace el personaje para dar la
vuelta de campana?

3. 30/04/13 Yuri Milachay 3
Lluvia de ideas
1. ¿Cómo llega la persona a alcanzar alturas tan
altas desde la posición de equilibrio?
2. ¿Con qué ejerce las fuerzas que provocan la
oscilación forzada?

4. 30/04/13 Yuri Milachay 4
Objetivos
1. Deduce una expresión para la 2° ley de
Newton que corresponde a la descripción de
las oscilaciones forzadas.
2. Aplica la expresión de la amplitud para
predecir las condiciones para que exista
resonancia.

5. 30/04/13 Yuri Milachay 5
max dF(t) F cos( t)= ω
Oscilaciones forzadas y
resonancia
• Un oscilador armónico
amortiguado aislado dejará
de moverse, pero podemos
mantener una oscilación de
amplitud constante
aplicando una fuerza que
varíe con el tiempo
periódicamente, con un
periodo definido.
• La solución de la ecuación es
la expresión:
max dF kx bv F cos( t)= − − + ω∑
x Asen( t )= ω + φ
max
2
2 2 2
0
F
mA
b
( )
m
=
ω 
ω − ω +  ÷
 
0 k /mω =

6. 30/04/13 Yuri Milachay 6
Oscilaciones forzadas y
resonancia
• La frecuencia angular para la
que la amplitud es máxima se
llama frecuencia de resonancia.

7. 30/04/13 Yuri Milachay 7
Caso: Puente Tacoma Narrow

8. 30/04/13 Yuri Milachay 8
Ejercicios
Una fuerza impulsora senoidal
se aplica a un oscilador
armónico amortiguado con
constante de fuerza k y una
masa m . Si la constante de
amortiguación vale b1, la
amplitud es A1 cuando la
frecuencia angular impulsora es
(k/m)1/2
. En términos de A1,
¿cuánto vale la amplitud con la
misma frecuencia impulsora y la
misma amplitud de la fuerza
impulsora Fmáx si la constante de
amortiguación es 3b?
max
1
1
F
A
b
=
ω
1
2
A
A
3
=
Solución.
2
0
k
;
m
ω = 1b
max
1 2
2 2 2 1
0 0
F
mA
b
( )
m
=
ω 
ω − ω +  ÷
 

9. 30/04/13 Yuri Milachay 9
Ejercicio
La estructura de soporte que
se colocó a bordo de la
estación espacial actúa como
sistema resorte-masa
subamortiguado con
constante de fuerza 2,10 x 106
N/m y masa 108 kg. Un requisito
de la NASA es que no haya
resonancia para oscilaciones
forzadas en ninguna frecuencia
menor que 35,0 Hz, ¿satisface el
paquete tal requisito? Es decir,
¿tiene frecuencias naturales
coincidentes?
• Solución
0f 22,2Hz=
0
k
m
ω =
6
0 (2,10 10 N m) 108kg)ω = ×
0
rad
139
s
ω =

10. 30/04/13 Yuri Milachay 10
Conclusiones
1. Describe matemáticamente las oscilaciones
forzadas.
2. Explica la relación entre la amplitud de
oscilación y la frecuencia natural de oscilación
del oscilador.
3. Se aplica la expresión de la amplitud para
predecir el movimiento de un cuerpo
sometido a oscilaciones forzadas.