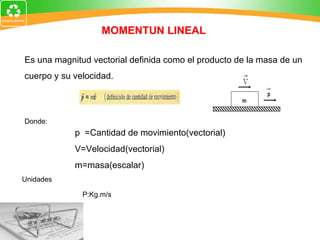
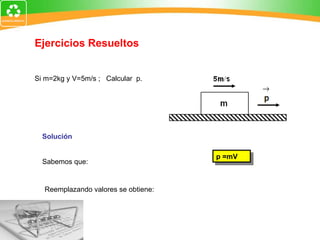
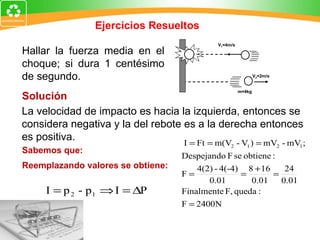
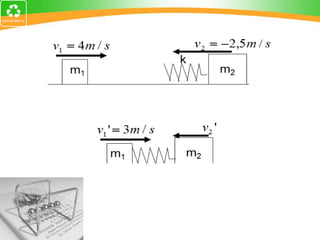
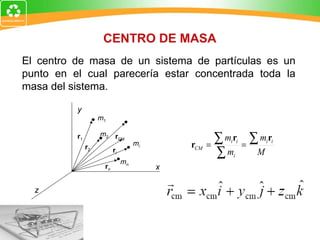
1. La cantidad de movimiento es una magnitud vectorial definida como el producto de la masa de un cuerpo y su velocidad.
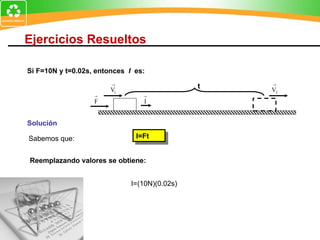
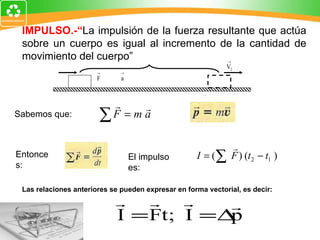
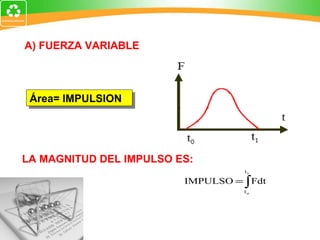
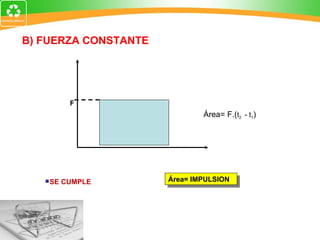
2. El impulso es una magnitud vectorial definida como el producto de la fuerza que actúa sobre un cuerpo y el intervalo de tiempo que dura la acción de la fuerza.
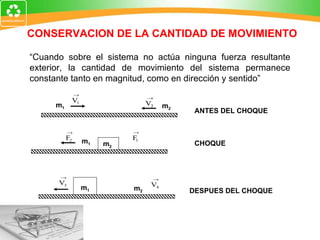
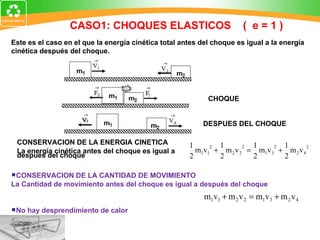
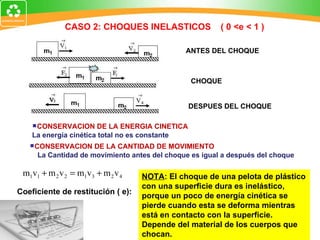
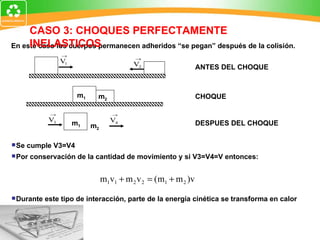
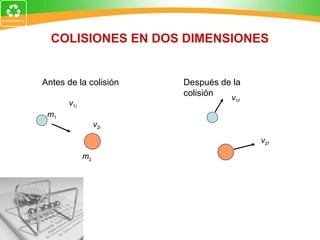
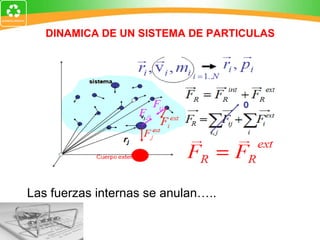
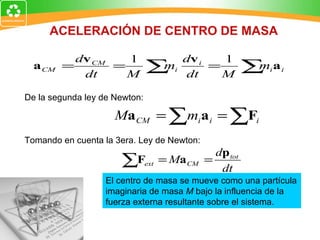
3. La ley de conservación de la cantidad de movimiento establece que la cantidad de movimiento total de un sistema permanece constante si no actúan fuerzas externas.