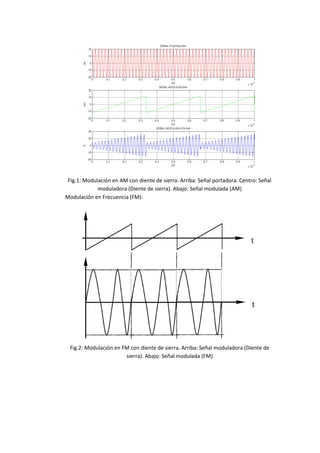
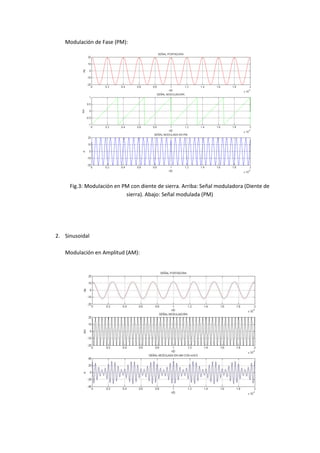
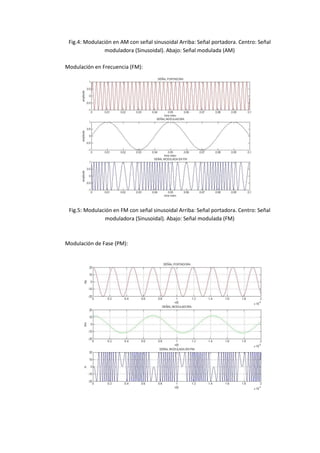
Este documento presenta la solución a 4 problemas relacionados con la modulación angular. El primer problema calcula parámetros como la potencia de una señal modulada en FM, la desviación de fase y frecuencia máximas. El segundo problema determina el ancho de banda necesario para una transmisión de FM comercial. El tercer problema grafica formas de onda moduladas con señales diente de sierra y sinusoidales. El cuarto problema compara el ancho de banda necesario para moduladores FM y PM usando diferentes frecuencias modulantes.

1. Modulación Angular
FEBRERO 2017
REPÚBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
EXTENSIÓN MATURIN
Bachiller: Víctor Díaz
Profesor:

2. Ejercicios Resueltos
PROBLEMA Nº1:
Dada la siguiente forma de onda modulada en FM:
𝜑 𝐹𝑀(𝑡) = 100cos⁡[2𝜋 ∗ 107
𝑡 + 30𝑠𝑒𝑛(2𝜋 ∗ 1000𝑡)]
Calcular:
1. Potencia normalizada de la portadora sin modular. (Pot. media)
2. Potencia normalizada de la onda modulada. (Pot. media)
3. Máxima desviación de fase.
4. Máxima desviación de frecuencia.
5. BW. y Nº. de bandas laterales.
6. Si la amplitud de la modulante se reduce en 100 veces y la frecuencia varía a 5 KHz,
cual es el nuevo BW (ancho de banda), cual es la potencia media normalizada de la
portadora modulada
Solución:
1. En primera instancia definimos la potencia de una señal FM según:
𝑃𝜑 𝐹𝑀
=
𝐴 𝑐
2
𝑇
∫|cos⁡( 𝑤𝑡)|2
𝑑𝑡
𝑇
2
−
𝑇
2
=
𝐴 𝑐
2
2
Entonces, la potencia normalizada de la portadora sin modular será:
𝑃𝜑 𝐹𝑀
⌋sin 𝑚𝑜𝑑𝑢𝑙𝑎𝑟
=
𝐴 𝑐
2
2
=
1002
2
= 5⁡KW
2. Una de las principales características que tiene este tipo de modulación es que la
potencia de la señal se mantiene constante, haya o no haya mensaje. Por lo tanto, la
potencia de la señal modulada será exactamente igual que la sin modular del punto
anterior:
𝑃𝜑 𝐹𝑀
⌋
con 𝑚𝑜𝑑𝑢𝑙𝑎𝑐𝑖ó𝑛
=
𝐴 𝑐
2
2
=
1002
2
= 5⁡KW
3. El desvío de fase (𝜃(𝑡)) es:
30𝑠𝑒𝑛(2𝜋 ∗ 1000𝑡)
Por lo tanto, el máximo desvío será cuando 𝑠𝑒𝑛(2𝜋 ∗ 1000𝑡) valga uno:
𝜃(𝑡) 𝑚𝑎𝑥
= 30
4. Sabiendo que:

3. 𝛽 =
∆𝑓
𝑓𝑚
= 30
Donde 𝑓𝑚 = 1000⁡𝐻𝑧
Se deduce que la máxima desviación de frecuencia es ∆𝑓 = 30⁡𝐾𝐻𝑧
5. El ancho de banda (B.W.) para señales de FM se define de la siguiente manera (Regla
de Carson)1
:
𝐵. 𝑊. = 2𝑁(𝛽) 𝑓𝑚
Donde 𝑁(𝛽) es el número de bandas laterales significativas, y se define como:
𝑁(𝛽) = 𝛽 + 𝛼
Siendo 𝛼 = (0; 1; 2; 3) según la calidad de transmisión. En este caso consideramos
𝛼 = 0. Entonces, el número de bandas laterales significativas será:
𝑁(𝛽) = 𝛽 = 30
Y el ancho de banda:
𝐵. 𝑊. = 2𝑁(𝛽) 𝑓𝑚 = 60⁡𝐾𝐻𝑧
6. Al reducir 100 veces la amplitud de la señal modulante, el desvío de frecuencia
también se verá reducido esa cantidad ya que el mismo es directamente proporcional
a la amplitud de dicha señal:
∆𝑓 = 𝑘 𝑓 𝐴 𝑚
Definimos entonces los tres nuevos parámetros:
∆𝑓′
=
∆𝑓
100
1
La regla de Carson es una regla general conocida en telecomunicaciones referente al ancho de banda, y que establece que
aproximadamente toda la potencia (~98%) de una señal consistente en una portadora senoidal modulada en frecuencia está
comprendida dentro de un ancho de banda (alrededor de la frecuencia portadora) de
𝐵. 𝑊. = 2𝑁(𝛽) 𝑓 𝑚 ; 𝑁(𝛽) = (𝛽 + 𝛼) ; 𝛼 = {
2,⁡⁡⁡⁡⁡⁡1 < 𝛽 ≤ 5
1,⁡⁡⁡5 < 𝛽 ≤ 20
0,⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡𝛽 > 20
donde 𝑁(𝛽) es la desviación máxima de la frecuencia instantánea f(t) (que es un efecto de modular en frecuencia, al igual que en
Amplitud Modulada (AM) se define el índice de modulación respecto a la amplitud) respecto a la portadora fc (asumiendo que
xm(t) está normalizada en el rango ±1), y donde fm es el ancho de banda de la señal moduladora (que se define "en banda base" y
es el mismo para la señal modulada). (Fuente: Wikipedia)

4. 𝑓𝑚
′
= 5𝐾𝐻𝑧
𝛽′
=
∆𝑓′
𝑓 𝑚′
=
∆𝑓
100∗𝑓 𝑚′
=
30⁡𝐾𝐻𝑧
100∗5𝐾𝐻𝑧
= 0,06
Dado que 𝛽′
= 0,06 en este caso tenemos una señal modulada en FM de banda
angosta (NBFM). Para este tipo de señales, el espectro resultante solo contiene
componentes de frecuencia en 𝜔𝑐 ± 𝜔 𝑚, por lo tanto el ancho de banda será:
𝐵. 𝑊. = 2𝑓𝑚 = 10⁡𝐾𝐻𝑧
Como ya mencionamos anteriormente, la potencia en FM es constante con y sin
modulación, por lo tanto:
𝑃𝜑 𝑁𝐵𝐹𝑀
⌋
𝑐𝑜𝑛⁡𝑚𝑜𝑑𝑢𝑙𝑎𝑐𝑖ó𝑛
=
𝐴 𝑐
2
2
=
1002
2
= 5⁡KW
Se aprecia claramente que la potencia solo depende de la amplitud de la portadora,
por lo tanto en este caso se mantiene invariante.
PROBLEMA Nº2:
Teniendo en cuenta que en la radiodifusión de FM se ha reglamentado el uso de una
desviación de frecuencia de 75 KHz y una señal modulante cuya frecuencia puede variar entre
30 y 15000 Hz.
Determinar:
1. El ancho de banda necesario para este tipo de transmisión, teniendo en cuenta que se
desea una alta calidad de recepción.
2. Comprobar que toda la banda de frecuencia posible de la señal modulante, produzca
un BW de señal modulada que cumpla con las especificaciones
Solución:
1. Para calcular el ancho de banda que necesita una transmisora de FM que cumple con
los requisitos reglamentados, debemos analizar lo que ocurre cuando la señal
modulante es de frecuencia mínima (30 Hz) y cuando es de frecuencia máxima (15
KHz). Para esto calculamos el 𝛽 𝑚𝑖𝑛 y el 𝛽 𝑚𝑎𝑥 :
𝛽 𝑚𝑎𝑥 =
∆𝑓
𝑓 𝑚𝑖𝑛
=
75000⁡𝐻𝑧
30⁡𝐻𝑧
= 2500
𝛽 𝑚𝑖𝑛 =
∆𝑓
𝑓𝑚𝑎𝑥
=
75000⁡𝐻𝑧
15000⁡𝐻𝑧
= 5
FM de banda angosta
(NBFM)

5. Ahora calculamos el ancho de banda para los valores de 𝛽 𝑚𝑎𝑥 y 𝛽 𝑚𝑖𝑛 utilizando la
Regla de Carson:
𝐵. 𝑊. ⌋ 𝛽 𝑚𝑎𝑥
= 2𝛽 𝑚𝑎𝑥 𝑓 𝑚𝑖𝑛 = 2 ∗ 2500 ∗ 30⁡𝐻𝑧 = 150⁡𝐾𝐻𝑧 = 2∆𝑓
𝐵. 𝑊. ⌋ 𝛽 𝑚𝑖𝑛
= 2(𝛽 𝑚𝑖𝑛 + 2)𝑓𝑚𝑎𝑥 = 2 ∗ 7 ∗ 15000⁡𝐻𝑧 = 210⁡𝐾𝐻𝑧 = 2∆𝑓 + 4𝑓𝑚𝑎𝑥
2. Como se puede apreciar en el punto anterior, el mayor ancho de banda necesario es
de 210 KHz, y se corresponde al 𝛽 𝑚𝑖𝑛 que implica una 𝑓𝑚𝑎𝑥 de 15 KHz. Dado que por
normativa el ancho de banda para transmisoras de FM comercial no puede superar los
200 KHz, lo que se hace es filtrar en alta frecuencia a la señal (filtro para señales de
gran potencia). Para cumplir con la norma, la frecuencia máxima de la señal
moduladora (𝑓𝑚𝑎𝑥) debería ser:
200⁡𝐾𝐻𝑧 = 2∆𝑓 + 4𝑓𝑚𝑎𝑥
𝑓𝑚𝑎𝑥 =
200⁡𝐾𝐻𝑧 − 2 ∗ 75⁡𝐾𝐻𝑧
4
= 12,5⁡𝐾𝐻𝑧
PROBLEMA Nº3:
Dibujar la representación temporal de una portadora modulada para los casos de AM, FM, y
PM (ω 𝑐 ⁡>>⁡ω 𝑚 𝑚𝑎𝑥
) si la señal modulante es una onda:
1. Diente de sierra
2. Sinusoidal
Solución:
1. Diente de sierra
Modulación en Amplitud (AM):

6. Fig.1: Modulación en AM con diente de sierra. Arriba: Señal portadora. Centro: Señal
moduladora (Diente de sierra). Abajo: Señal modulada (AM)
Modulación en Frecuencia (FM):
Fig.2: Modulación en FM con diente de sierra. Arriba: Señal moduladora (Diente de
sierra). Abajo: Señal modulada (FM)

7. Modulación de Fase (PM):
Fig.3: Modulación en PM con diente de sierra. Arriba: Señal moduladora (Diente de
sierra). Abajo: Señal modulada (PM)
2. Sinusoidal
Modulación en Amplitud (AM):

8. Fig.4: Modulación en AM con señal sinusoidal Arriba: Señal portadora. Centro: Señal
moduladora (Sinusoidal). Abajo: Señal modulada (AM)
Modulación en Frecuencia (FM):
Fig.5: Modulación en FM con señal sinusoidal Arriba: Señal portadora. Centro: Señal
moduladora (Sinusoidal). Abajo: Señal modulada (FM)
Modulación de Fase (PM):

9. Fig.6: Modulación en PM con señal sinusoidal Arriba: Señal portadora. Centro: Señal
moduladora (Sinusoidal). Abajo: Señal modulada (PM)
PROBLEMA Nº4:
Se dispone de un generador de señal cosenoidal x(t)⁡= ⁡cos⁡(2π⁡fm⁡t), cuya frecuencia puede
adoptar tres valores diferentes: fm1= 0,1kHz; fm2 =1 kHz y fm3 = 5 kHz.
Dicha señal será utilizada para realizar un ensayo sobre un modulador de FM, con una
constante del modulador 𝐾𝑓 = ⁡30⁡kHz/volt⁡ al cual se aplica alternadamente cada uno de los
tonos. Luego se repite el mismo ensayo sobre un modulador de PM cuya constante es 𝐾 𝑝 =
⁡30.
Se solicita:
1. Comparar el ancho de banda B necesario para cada modulador en cada uno de los
tres casos. Extraer conclusiones.
2. Determinar para que frecuencia modulante los B son iguales.
3. Considerando este último caso, B iguales, determinar las expresiones de la onda
modulada en frecuencia y fase en el caso de utilizar una portadora con las siguientes
características: c(t) = ⁡3⁡cos⁡(2π. 106⁡t⁡)
Solución:
1. En primer lugar vamos a definir las ecuaciones necesarias para calcular el ancho de
banda necesario para los dos tipos de moduladores, FM y PM.
Como se definió en el Problema Nº 1, el factor 𝛽 en FM se calcula como:
𝛽 𝐹𝑀 =
𝐾𝑓 ∗ 𝐴 𝑚
𝑓𝑚
=
30 ∗ 103
⁡𝐻𝑧/𝑉 ∗ 1⁡𝑉
𝑓𝑚
=
∆𝑓
𝑓𝑚
El ancho de banda B se definió según la Regla de Carson como:
𝐵 𝐹𝑀 = 2(𝛽 𝐹𝑀 + 1)𝑓𝑚 (𝛼 = 1)
Reemplazando
𝐵 𝐹𝑀 = 2𝐾𝑓 + 2𝑓𝑚
Para el caso de PM, el factor 𝛽 𝑃𝑀 se obtiene según:
𝛽 𝑃𝑀 = 𝐾 𝑝 ∗ 𝐴 𝑚
Luego, el ancho de banda 𝐵 𝑃𝑀será:

10. 𝐵 𝑃𝑀 = 2𝐾 𝑝 𝑓𝑚 + 2𝑓𝑚
Por lo tanto, para los 3 casos de cada modulador se obtienen los siguientes resultados:
ANCHO DE BANDA [B]
X1(t)0,1 kHz X2(t)1 kHz X3(t)5 kHz
MODULADOR FM 60,2 KHz 62 KHz 70 KHz
MODULADOR PM 800 Hz 8 KHz 40 KHz
Estos resultados reflejan una característica muy clara y distintiva entre ambos sistemas
de modulación: La relación entre frecuencia de la señal modulante y el ancho de banda
necesario para transmitirla es completamente distinta en PM con respecto a FM.
Mientras que en FM el ancho de banda varía entre 60,2 KHz y 70 KHz (diferencia de 9,8
KHz) para señales de entre 100 Hz y 5 KHz, en PM el ancho de banda varía entre 800 Hz
y 40 KHz (diferencia de 39,2 KHz) para el mismo rango de frecuencia de la señal
modulante.
Esto se debe a la naturaleza de cada tipo de modulación ya que se ve claramente que
el ancho de banda en PM aumenta de forma lineal con la frecuencia de la señal
moduladora, tal como lo indica la definición de este tipo de señales.
Por su parte, las señales de FM varían su frecuencia de forma no lineal, según la
integral de la modulante, motivo por el cual el ancho de banda sufre alteraciones más
pequeñas que en el caso de PM.
2. Los valores 𝛽 𝐹𝑀 y 𝛽 𝑃𝑀 serán iguales cuando se cumpla que:
2𝐾𝑓 + 2𝑓𝑚 = 2𝐾 𝑝 𝑓𝑚 + 2𝑓𝑚
𝑓𝑚 =
𝐾𝑓
𝐾 𝑝
Por lo tanto, la frecuencia de la señal modulante será 10⁡𝐾𝐻𝑧, y su ancho de banda
80⁡𝐾𝐻𝑧.
3. Utilizando entonces 𝑓𝑚 = 10⁡𝐾𝐻𝑧, obtenemos 𝛽 𝐹𝑀 y 𝛽 𝑃𝑀:
𝛽 𝐹𝑀 =
𝐾𝑓 ∗ 𝐴 𝑚
𝑓𝑚
=
30 ∗ 103
∗ 1𝑉
10 ∗ 103
= 3
𝛽 𝑃𝑀 = 𝐾 𝑝 ∗ 𝐴 𝑚 = 3 ∗ 1 = 3

11. Por lo tanto se obtienen:
𝜑 𝐹𝑀 = 3cos⁡[2𝜋 ∗ 106
𝑡 + 3 cos(2𝜋 ∗ 103
𝑡)]
𝜑 𝑃𝑀 = 3cos⁡[2𝜋 ∗ 106
𝑡 + 3 cos(2𝜋 ∗ 103
𝑡)]
Claramente se aprecia que debido a que los anchos de banda de cada tipo de
modulación son iguales, sus 𝛽 también lo son, por lo tanto las expresiones de 𝜑 𝐹𝑀y
𝜑 𝑃𝑀 coinciden.
PROBLEMA Nº5:
Una señal de ángulo modulado tiene un ⁡Δf 𝑚𝑎𝑥1 = ⁡20⁡Hz⁡ para una entrada senoidal de
amplitud unitaria y frecuencia 50 Hz.
Se solicita:
1. Si la modulación utilizada es FM. Determinar el factor de multiplicación N necesario
para producir un ⁡Δf 𝑚𝑎𝑥2 = ⁡20⁡KHz, cuando la frecuencia de la señal de entrada es de
100 Hz.
2. Ídem para PM.
Solución:
1. Debido a que la señal de entrada (modulante) tiene amplitud unitaria, el incremento N
necesario para ⁡Δf 𝑚𝑎𝑥 = ⁡20⁡KHz será:
∆𝑓 𝑚𝑎𝑥1⌋ 𝐹𝑀 = 𝐾𝑓 ∗ 𝐴 𝑚 = 20⁡𝐻𝑧
∆𝑓 𝑚𝑎𝑥2⌋ 𝐹𝑀 = 𝑁 ∗ ∆𝑓 𝑚𝑎𝑥1⌋ 𝐹𝑀 = 𝑁 ∗ 20⁡𝐻𝑧
20⁡𝐾𝐻𝑧 = 𝑁 ∗ 20⁡𝐻𝑧
𝑁 = 1000
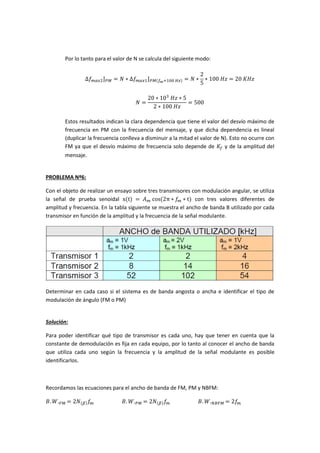
2. Para el caso de PM, se debe considerar la frecuencia de la señal modulante (50 Hz), ya
que el desvío máximo de frecuencia en este caso se define como:
∆𝑓 𝑚𝑎𝑥1⌋ 𝑃𝑀 = 𝐾 𝑝 ∗ 𝐴 𝑚 ∗ 𝑓𝑚 = 𝐾 𝑝 ∗ 𝑓𝑚 = 20⁡𝐻𝑧
𝐾 𝑝 =
20⁡𝐻𝑧
𝑓𝑚
=
20⁡𝐻𝑧
50⁡𝐻𝑧
=
2
5

12. Por lo tanto para el valor de N se calcula del siguiente modo:
∆𝑓 𝑚𝑎𝑥2⌋ 𝑃𝑀 = 𝑁 ∗ ∆𝑓 𝑚𝑎𝑥1⌋ 𝑃𝑀(𝑓 𝑚=100⁡𝐻𝑧) = 𝑁 ∗
2
5
∗ 100⁡𝐻𝑧 = 20⁡𝐾𝐻𝑧
𝑁 =
20 ∗ 103
⁡𝐻𝑧 ∗ 5
2 ∗ 100⁡𝐻𝑧
= 500
Estos resultados indican la clara dependencia que tiene el valor del desvío máximo de
frecuencia en PM con la frecuencia del mensaje, y que dicha dependencia es lineal
(duplicar la frecuencia conlleva a disminuir a la mitad el valor de N). Esto no ocurre con
FM ya que el desvío máximo de frecuencia solo depende de 𝐾𝑓 y de la amplitud del
mensaje.
PROBLEMA Nº6:
Con el objeto de realizar un ensayo sobre tres transmisores con modulación angular, se utiliza
la señal de prueba senoidal x(t)⁡=⁡ 𝐴 𝑚⁡cos(2π ∗ 𝑓𝑚 ∗ t) con tres valores diferentes de
amplitud y frecuencia. En la tabla siguiente se muestra el ancho de banda B utilizado por cada
transmisor en función de la amplitud y la frecuencia de la señal modulante.
Determinar en cada caso si el sistema es de banda angosta o ancha e identificar el tipo de
modulación de ángulo (FM o PM)
Solución:
Para poder identificar qué tipo de transmisor es cada uno, hay que tener en cuenta que la
constante de demodulación es fija en cada equipo, por lo tanto al conocer el ancho de banda
que utiliza cada uno según la frecuencia y la amplitud de la señal modulante es posible
identificarlos.
Recordamos las ecuaciones para el ancho de banda de FM, PM y NBFM:
𝐵. 𝑊. 𝐹𝑀 = 2𝑁(𝛽) 𝑓𝑚 𝐵. 𝑊. 𝑃𝑀 = 2𝑁(𝛽) 𝑓𝑚 𝐵. 𝑊. 𝑁𝐵𝐹𝑀 = 2𝑓𝑚

13. 𝐵. 𝑊. 𝐹𝑀 = 2(𝛽 + 1)𝑓𝑚 𝐵. 𝑊. 𝑃𝑀 = 2(𝛽 + 1)𝑓𝑚⁡
𝐵. 𝑊. 𝐹𝑀 = 2𝛽𝑓𝑚 + 2𝑓𝑚 𝐵. 𝑊. 𝑃𝑀 = 2𝛽𝑓𝑚 + 2𝑓𝑚⁡
𝐵. 𝑊. 𝐹𝑀 = 2𝐾𝑓 𝐴 𝑚 + 2𝑓𝑚 𝐵. 𝑊. 𝑃𝑀 = 2𝐾 𝑝 𝐴 𝑚 𝑓𝑚 + 2𝑓𝑚
Ahora se elige uno de estos tres tipos de modulaciones y se evalúa en qué transmisor la
constante de demodulación se mantiene invariable a los cambios de frecuencia y amplitud de
la señal modulante.
 Evaluamos 𝐾𝑓 para el transmisor 3:
Se observa que 𝐾𝑓 se mantiene constante en cada caso, por lo tanto el transmisor 3 es
de FM.
 Evaluamos 𝐾 𝑝 para el transmisor 2:
En este caso el valor de 𝐾 𝑝 se mantiene invariante, por lo tanto el transmisor 2 es de
PM.
 Para el transmisor 1 se cumple que 𝐵. 𝑊. 𝑁𝐵𝐹𝑀 = 2𝑓𝑚, entonces el mismo es de NBFM.