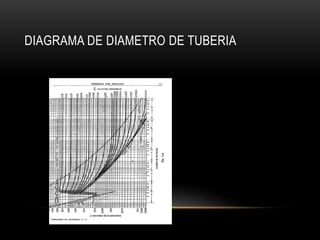
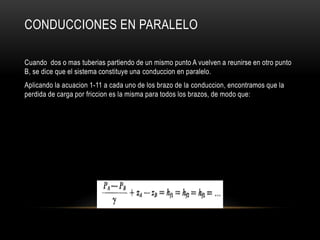
Este documento trata sobre operaciones unitarias relacionadas al transporte de fluidos. Explica conceptos clave como caudal, velocidad, densidad y ecuaciones para calcular pérdidas por fricción. También cubre temas como diámetros mínimos de tubería, conducciones en paralelo y factores que afectan el régimen laminar o turbulento de un fluido.

1. OPERACIONES UNITARIAS I
ALUMNO:JUAN MANUEL ARUQUIPA
CODIGO:9356-7
RESUMEN….
PROBLEMAS DE INGENIERIA QUIMICA

2. INTRODUCCION
• TRANSPORTE DE FLUIDOS:
Esto se lleva a cabo por aplicación de balances de materia y energia y
haciendo uso de relaciones deducidas de modo empirico referentes a la friccion
de los fluidos.}
Aplicando la ley de conservacion de la masa a dos puntos de una canalizacion,
se llega a la cantidad de materia que pasa por ambos puntos en la unidad de
tiempo es la misma, si designamos por A el area de la seccion normal al flujo,
por p la densidad del fluido y por µ su velocidad podremos escribir para puntos
1 y 2:
A1 µ1p1 = A2µ2p2

3. INTRODUCCION
Donde:
A: Area
µ: Velocidad
p: Densidad
Y esta funcion puesta en funcion del volumen especifico
V se convierte en:

4. INTRODUCCION
Donde el producto A * u = Q se denomina gasto o caudal.
La relacion u/V= G se denomina velocidad masica .
Y el cociente Q/V = W recibe el nombre de flujo de masa que puede escibrirse en la forma:

5. ECUACIONES GENERALES DE FLUJO
Si efectuamos un balance energetico entres los puntos 1 y 2 considerando la energia
transportada por el fluido y la transmitida entre el fluido y el entorno, llegamos a la expresion:

6. ECUACIONES GENERALES DE FLUJO
Donde :
q : Calor suministrado al fluido desde el entorno
W : Trabajo realizado por el fluido contra el entorno
Δ (PV) : Variación de energía de presión
Δ U: Variación de energía interna
Δ (mu/2g) : Variación de Energía cinética
Δ ( mgz/g) : Variación de Energía potencial

7. ECUACIONES GENERALES DE FLUJO
Entalpía: es una magnitud termodinámica, simbolizada
con la letra H mayúscula, cuya variación expresa una
medida de la cantidad de energía absorbida o cedida
por un sistema termodinámico, es decir, la cantidad de
energía que un sistema intercambia con su entorno.

8. ECUACIONES GENERALES DE FLUJO
Teniendo en cuenta la definicion de entalpia
( H= U + PV) , la ecuacion anterior se puede poner de la forma:

9. ECUACIONES GENERALES DE FLUJO
En las ecuciones de flujo tenemos una ecuacion que es usada comunmente que la conocida
Ecuacion De Bernouilli que esta expresada de la siguiente manera:

10. EJEMPLOS
Ejemplo 1 : En un cambiador de calor entra nitrogeno a 15°c a la velocidad media de 5
m/seg, saliendo del mismo a 30°C y a 20 m/seg. Si el lugar de salida se encuentra a
6 m por encima del de entrada y entre ambos puntos no existe bomba o turbina alguna ,
calculense:
• La cantidad de calor suministrado para elevar la temperatura.

11. EJEMPLOS
• La variacion de su energia cinetica
• La variacion de su energia potencial
• La cantidad total de calor suministrado
El calor especifico molar para el nitrogeno en este intervalo de temperaturas viene dado por
Cp= 6.50 + = 0.0010 T).

12. EJEMPLOS
SOLUCION:
Refieriendo a los calculos a 1 kg de nitrogeno:

13. PERDIDAS POR FRICCIÓN
Para la aplicación de ciertas ecuaciones es necesaria la evaluacion del termino
correspondiente a la friccion. La aplicación del analisis dimensional al estudio de este termino
nos conduce a la expresion:

14. PERDIDAS POR FRICCIÓN
Donde:
ƒ: Factor o coeficiente de friccion
L: Longitud total de canalizacion
D: Diametro
µ: Velocidad lineal media

15. PERDIDAS POR FRICCIÓN
Indiquemos que el estudio de mecanismo de la circulacion de fluidos nos lleva a considerar
dos tipos de flujo: Laminar o Viscoso Cuando el flujo es paralelo a las paredes. Estas
magnitudes se agrupan en un modulo adimensional, denominado modulo o indice de
Reynolds definido por la expresion:

16. PERDIDAS POR FRICCIÓN
Que nos caracteriza el tipo de flujo, ya que existe un valor de Re denominado Reynolds
Critico y que corresponde aproximadamente a 2100, que marca la separación entre el flujo
laminar y el turbulento, de tal manera que cuando Re es menor que este valor, el régimen de
flujo es laminar.

17. PERDIDAS POR FRICCIÓN
La distribucion de velocidades a lo largo de un diametro es distinta según se trate de flujo
laminar o turbulento:
Regimen Laminar:

18. PERDIDAS POR FRICCION
Regimen Turbulento:

19. LONGITUD EQUIVALENTE
LA Ec 1-13 se refiere a la perdida por la friccion para una tuberia recta a lo largo de una
longitud L, considerando que lla tuberia no tiene tipo alguno de accesorios, tales como
llaves, codos, empalmes, etc.

20. FACTOR O COEFICIENTE DE FRICCION
Cuando se trata de regimen laminar se puede deducir facilmente que este factor viene
dado por la expresion :

21. FACTOR O COEFICIENTE DE FRICCION
Para el regimen turbulento este factor se determina en funcion del Re y de la rugosidad
relativa €/D; se define a la rugosidad como el cociente entre el espesor de las irregularidades
de la cara interna del tubo y el diametro interno del mismo.

22. FACTOR O COEFICIENTE DE FRICCION
La determinacion practica de este factor cuando se conocen las propiedades fisicas del
fluido( densidad y viscosidad), las caracteristicas de la tuberia ( diametro y longitud) y el
caudal del fluido se lleva a cabo del modo siguiente:
1. Se determina la velocidad a partir del diametro y el caudal
2. Se calcula el Re
3. Se determina €/D en la grafica 1-3
4. Se determina ƒ en la grafica 1-4
5. Se determina la longitud equivalente en la figura 1-2
6. Se calcula Hf haciendo uso de la Ec. 1-13

23. DIAGRAMA DE DIAMETRO DE TUBERIA

24. DIAGRAMA DE DIAMETRO DE TUBERIA

25. CALCULO DE DIAMETRO MINIMO
Un problema con el que nos encontramos frecuentemente es de la determinacion del
diametro minimo de tuberia a emplear, disponiendo de una carga determinada para el
desplazamiento de un caudal conocido.
En este caso la resolucion del problema se lleva a cabo del modo siguiente:

26. CALCULO DE DIAMETRO MINIMO
1. Se pone la velocidad en funcion del caudal y el diametro.
2. Se destruye el valor de la velocidad en la Ec 1-13, quedando como acuacion resultante.

27. CALCULO DE DIAMETRO MINIMO
3.- Se efectua el calculo por tanteo suponiendo un valor F1 determinando D1 por la Ec. 1-23
4.- Se determinan Re y €/D para el valor de D1
5.- Se determina el valor de f en funcion de Re y €/D con ayuda de la figura 1-4.

28. CONDUCCIONES EN PARALELO
Cuando dos o mas tuberias partiendo de un mismo punto A vuelven a reunirse en otro punto
B, se dice que el sistema constituye una conduccion en paralelo.
Aplicando la acuacion 1-11 a cada uno de los brazo de la conduccion, encontramos que la
perdida de carga por friccion es la misma para todos los brazos, de modo que:

29. CONDUCCIONES EN PARALELO
Por otra parte, ha de cumplirse que el caudal total que circula por el sistema ha de ser igual a
la suma de los caudales que circulan a traves de los diversos brazos:
Q = Q1 + Q2 +Q3 …………
Fin De resumen……… Continuara……….

30. ANEXOS
TRANSPORTE DE FLUIDOS: ( Sistema Abierto)

31. ANEXOS