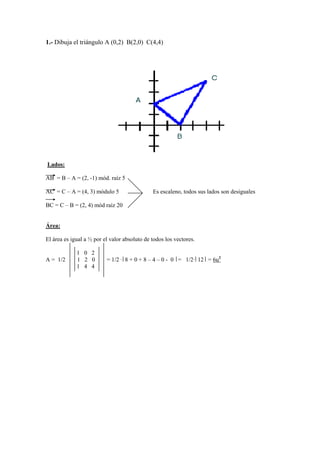
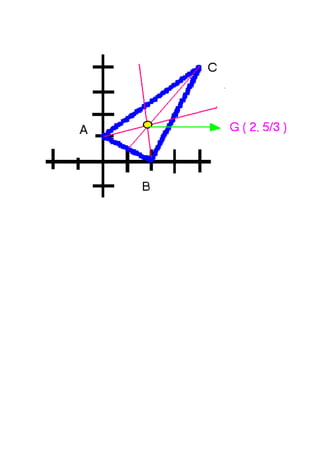
Este documento proporciona instrucciones para dibujar y analizar un triángulo escaleno ABC. Calcula las longitudes de los lados, el área, las alturas, la mediana, el baricentro y el circuncentro. Resume que el triángulo ABC tiene coordenadas (0,2), (2,0) y (4,4), y que sus medidas y puntos notables como el baricentro (2,5/3) y el circuncentro (2,5/2) se calculan a través de fórmulas geométricas.

1. 1.- Dibuja el triángulo A (0,2) B(2,0) C(4,4)
Lados:
AB = B – A = (2, -1) mód. raíz 5
AC = C – A = (4, 3) módulo 5 Es escaleno, todos sus lados son desiguales
BC = C – B = (2, 4) mód raíz 20
Área:
El área es igual a ½ por el valor absoluto de todos los vectores.
1 0 2
A = 1/2 1 2 0 = 1/2 · 8 + 0 + 8 – 4 – 0 - 0 = 1/2· 12 = 6u2
1 4 4

2. Distancias alturas:
hA Es la recta que pasa por un vértice y es perpendicular al lado opuesto de dicho vértice.
A = ( 0,1 )
B = ( 2, 0 ) x–2 y–0
V BC 2 = 4 4x –8 = 2y 2(2x – y –4)
BC = (2, 4 )
0–1–4 -5 5
d ( A, VBC ) = = = u
4 +1 5 5
hB
B = ( 2, 0 )
A = ( 0, 1 ) x–0 y–1
= 3x – 4y + 4 = 0
VAC 4 3
AC = ( 4, 3 )
6+0+4 10
d ( A, VBC ) = = u
9 + 16 25

3. Baricentro: Es el punto por donde confluyen las medianas. Para calcularlo, previamente
debemos de haber calculado al menos dos de las madianas.
mA Recta que une un vértice con el punto medio del lado opuesto.
MBC = ( 6/2, 4/2 ) = ( 3, 2 )
x–0 y–1
A = ( 0, 1 ) mA = =
3 1
v = BC – A = ( 3, 1 )
mB
MAC = ( 4/2, 5/2 ) = ( 2, 5/2 )
x–2 y–0
B = ( 2, 0 ) mB = =
0 5/2
v= AC – B = ( 0, 5/2 )
Baricentro:
mA = x - 3y + 3 = 0
mB = 5/2x – 5 = 0 x = 5: 5/2 = 10/5 = 2 2 – 3y + 3 = 0 y = 5/3
G = ( 2, 5/3 )

5. Circuncentro: Es el punto donde confluyen las madiatrices. Para calcularlo previamente
debemos de haber calculado al menos dos de las mediatrices.
μAB Recta perpendicular al punto medio de un lado.
MAB = ( 2/2, 1/2 ) = ( 1, 1/2 )
AB = (2, -1 ) ( 2, -1 ) ( 1, 2 ) = 0
x–1 y – 1/2
μAB = =
1 2
μBC
MBC = ( 3, 2 )
BC = ( 2, 4 ) ( 2, 4 ) ( 2, -1 ) = 0
x–3 y–2
μBC = =
2 -1
Circuncentro:
μAB = 2x – y – 3/2 = 0 ( -1 ) 4x – 2y – 3 = 0 -4x + 2y + 3 = 0
μAB = -x – 2y + 7 = 0 -x –2y + 7 = 0 -x –2y + 7 = 0
-5x + 10 = 0 x=2
-2 – 2y + 7 = 0 y = 5/2
C = ( 2, 5/2 )