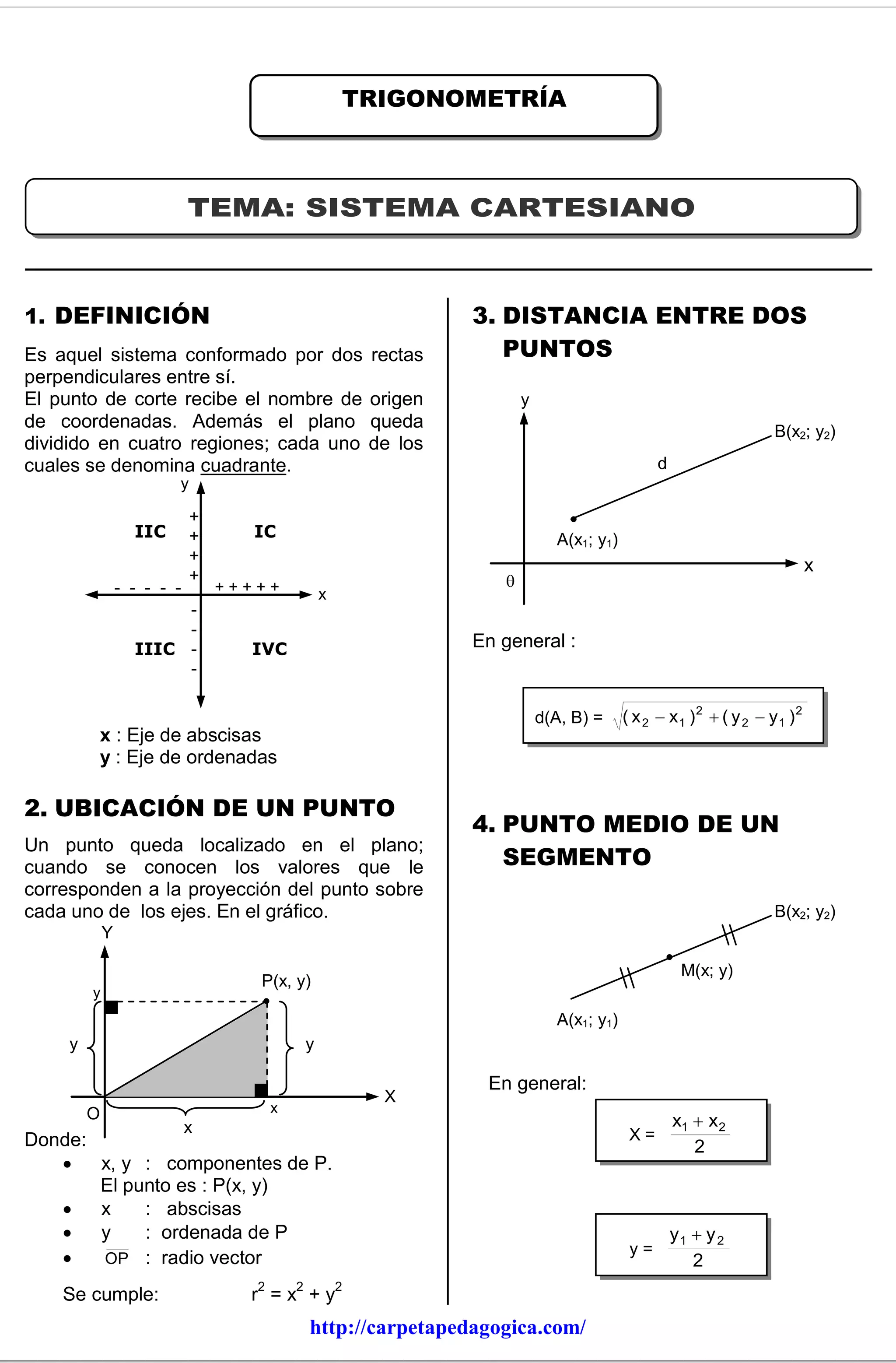
Este documento presenta los conceptos básicos del sistema cartesiano, incluyendo la definición, la ubicación de puntos, la distancia entre puntos, el punto medio de un segmento y la propiedad del baricentro. También resuelve seis problemas de trigonometría que aplican estos conceptos para calcular distancias, coordenadas y lados de triángulos.

1. TRIGONOMETRÍA
TEMA: SISTEMA CARTESIANO
1. DEFINICIÓN 3. DISTANCIA ENTRE DOS
Es aquel sistema conformado por dos rectas PUNTOS
perpendiculares entre sí.
El punto de corte recibe el nombre de origen y
de coordenadas. Además el plano queda B(x2; y2)
dividido en cuatro regiones; cada uno de los
cuales se denomina cuadrante. d
y
+
IIC + IC A(x1; y1)
+
x
+ 
- - - - - +++++ x
-
-
IIIC - IVC En general :
-
d(A, B) = ( x 2  x1 )2  ( y 2  y1 )2
x : Eje de abscisas
y : Eje de ordenadas
2. UBICACIÓN DE UN PUNTO
4. PUNTO MEDIO DE UN
Un punto queda localizado en el plano;
cuando se conocen los valores que le SEGMENTO
corresponden a la proyección del punto sobre
cada uno de los ejes. En el gráfico. B(x2; y2)
Y
M(x; y)
P(x, y)
y
A(x1; y1)
y y
En general:
X
O x
x x1  x 2
Donde: X=
2
 x, y : componentes de P.
El punto es : P(x, y)
 x : abscisas
 y : ordenada de P y1  y 2
y=
 OP : radio vector 2
2 2 2
Se cumple: r =x +y
http://carpetapedagogica.com/

2. 5. PROPIEDAD DEL DC
P  3 AC 26  AB 41  8
BARICENTRO 5
B(x2; y2)
Solución:
A ( 2, 5) ; B(7; 9), C(-3; 4)
G(x, y)
BC
A(x1; y1) P= 3 AC 26  AB 41  8
C(x3, y3) 5
Donde: Por distancia entre 2 puntos :
G  Baricentro  AC = 2  5)2  (5  4)2  26
En general :  AB = 2  7)2  (5  9)2  41
 BC = 7  3)2  (9  4)2  125  5 5
x1  x 2  x 3
X=
3
5 5
P= 3 26 x 26 x 41 x 41  8 x
5
y1  y 2  y 3 P= 3
27 P=3
y=
3
3).- Si dos vértices de un triángulo son A(-4, 6)
y B(-3, 8). Hallar la suma de las
PROBLEMAS RESUELTOS coordenadas del tercer vértice sabiendo que
las medianas de dicho triángulo se
intersectan en el punto P(2, 6)
1).- La distancia entre los puntos (2, 1) y (5, 4)
Solución :
es K 6 . Calcula “k”.
Solución : Dato : A(-4. 6) ; B(-3, 8) ; C(x ,y)
 P(2, 6)  Baricentro
Dato : (2, 1) y (5, 4)
Se sabe que la distancia entre los Se sabe :
puntos :
d= (5  2)2  ( 4  1)2 ( 4)  ( 3)  x
=2 x = 13
3
d = 18
68y
Por dato: 6 y=4
3
k 6 = 18
18 x + y = 17
k=
6
k= 3
4).- De la figura, halla “a” si AB//MN.
2).- Dados los puntos:
B(1, 8)
A(2, 5) B(7, 9) C(-3; 4)
M(4, 6)
Halla:
C(7, 4)
(-2, a) A
http://carpetapedagogica.com/ N(5/2, 3)

3. Solución:
Por el punto medio de un segmento: 6).- Cuál es el mayor lado de un triángulo
cuyos vértices son:
a4 A(-1; 3), B(2; 5) y C(4; -1)?
3
2
a+4=6  a=2 Solución:
y
5).- ¿Qué punto está más alejado del 5 B(2; 5)
origen?
a) A(1; 2) b) B(3; -1) c) C(2; 3) A(-1; 3)
3
d) D(4; 0) e) E(-3; 4)
Solución: y
E
4
4
C x
3 -1 2
2 -1 C(4; -1)
d(A; B) = (1  2)2  (3  5)2
1 3 4
2 D
x d(A; B) = (9  4  13
-3
-1 B d(B; C) = ( 4  2)2  (1  5)2
Hallando el radio-vector de cada punto: d(B; C) = (4  36)  40
rA = a2  22  5 d(A; C) = (1  4)2  (3  (1))2
rB = 32  (1)2  10 d(A; C) = 41
rC = 22  32  13  El lado mayor mide 41
2 2
rD = 4  0  16
rE = (3)2  42  25
 El punto más alejado es “E”
CUESTIONARIO
I. Coloca Verdadero (V) o falso(F) según corresponda :
 Sean los puntos A(x1, y1) ; B(x2, y2) y C(x3, y3) entonces :
2
1. La distancia entre A y B es d(A; B) = (x2 – x1) + (y2 – y1) (F )
x x y y 
2. Las coordenadas del punto medio del segmento BC son M 2 3 ; 2 3
 
 (V )
 2 3 
x1  x 2  x 3 y y y
3. Las coordenadas del baricentro del triángulo ABC son: x  ; y 1 2 3 (V )
3 3
 x1  x 2 y1  y 2 
4. Las coordenadas del punto medio del segmento AB son M 
 ; 
 (F )
 2 2 
5. La distancia entre los puntos B y C es : d(B, C) = ( x 3  x 2 )2  ( y 3  y 2 )2 (V )
http://carpetapedagogica.com/

4. II. Completa en los espacios vacíos:
cartesiano 4
1. El sistema .............................. está dividido en .............. cuadrantes.
primera
2. En el par (x, y ) la ........................... componente es la abscisa del punto.
componente ordenada del punto
3. En el par (x, y) la segunda ............................. es la..................................................................
radio vector
4. La distancia del origen de coordenada al punto P(x, y) se denomina : ....................................
III. Subraya la alternativa correcta :
1).- Dados los vértices consecutivos de 5).- Los vértices de un cuadrado son
un paralelogramo A=(1; 5), B(3; 4), A(1; 3); B(5; 3), C( m; n) y D(p; q).
C=(5; -1) y D=(x0y0). Calcular “x0 + y0”
Calcula:
a) 1 b) 3 c) 2
d) 4 e) 12 m + n + p + q. Si C y D no pertenecen
al IV C.
2).- Si las longitudes de los segmentos a) 10 b) 20 c) 15
AB y BC son iguales. Halle la suma de d) 24 e) 25
las coordenadas del punto C.
A = (1; 1) B = (5; 4)
C
6).- Dado el segmento AB cuyos lados
a) 6 son A = (1; 1) y B= (7; 7); ubicar un
b) 8 punto “P” en AB , tal que ; AP  5PB .
c) 10 B
d) 12 a) (2; 2) b) (3; 3) c) (4; 4)
e) 14 d) (5; 5) e) (6; 6)
A
3).- Calcula: AP // PB siendo ”p” el punto 7).- En el segmento AB halle un punto
de intersección del eje “y” con AB : “P” tal que : AP  3PB ; si A=(-2; -5) y
A = (-2; 1) y B = (3; 7) B=(2; 3)
a) ½ b) ¾ c) 2/3 a) (1; 0) b) (1; 1) c) (1; -1)
d) 4/5 e) 3/5 d) (1; 2) e) (0; 1)
4).- Del gráfico, calcular: “S” si : AM  MC
y 8).- Señala la ordenada de un punto “P”
2
a) 2u B(a, 5) cuya abcisa es 3; sabiendo que dista
b) 4 13u de Q(-2; 0)
P
c) 6
d) 8 A(-2, 1) a) 7 b) 5 c) 12
S Q
e) 10 x d) a y b e) b y c
M
C(4, b)
http://carpetapedagogica.com/

5. 9).- Si dos vértices de un cuadrado 15).- La distancia entre los puntos (2, -1)
ABCD son A(-1; 2) y D(2; 1). ¿Cuál es y (5, -5) es la misma que entre los
su perímetro? puntos (-3, 0) y (x, 3). Halla los
valores de “x”.
a) 10 b) 5 c) 5
a) –7 b) 1 c) 6
d) 20 e) 4 10
d) 4 e) {-7, 1}
10).- Por el punto A(4; 2) se ha trazado
una circunferencia tangente a los dos 16).- Si “O” es el centro de la
ejes de coordenadas. Determinar la circunferencia. Hallar dicho centro.
longitud máxima de dichas
circunferencias (=3,14) P
3a (4, 11)
2a
a) 3,14u b) 31,4 c) 314
N
d) 62,8 e) 12,56
(-1, 6)
O
11).- Si los vértices de un triángulo son
A(1; 1), B(2, 3) y C(5; 1), calcular la
longitud relativa de la misma mediana (5, -4)
relativa al lado AC .
a) (3,5) b) (0,6) c) (1, 1)
a) 5 b) 10 c) 15 d) (3, 2) e) (2, 3)
d) 17 e) 2 6
12).- Señale lo incorrecto. 17).- Calcular la coordenada del vértice
“C” en el paralelogramo ABCD.
a) (3; -2)  IV C b) (8; 2)  I C
C
c) (2; 19  I C d) (2; -3) v III C y
a) (6, 4) B(2, 3)
e) (3; 0)  eje “x” b) (5, 5)
c) (6, 5)
d) (5, 4)
13).- Los vértices de un triángulo son e) (3, 59 D(3, 1)
A=(1; 2), B=(3; 6) y C=(-1; 0). ¿Cuál es
la longitud de la mediana relativa al x
lado AB, su baricentro es: A
a) 5; (1, 8) b) 3; (1; 7)
c) 5; (1, 8/3) 18).- Los puntos A(1, 2) , B(4, 6) y C(12,
0) son los vértices de un triángulo.
Halle la coordenada del punto de
14).- Ubica en el eje “y”, un punto que intersección de la bisectriz interior que
diste : parte de “B” con el lado AC.
5u de P=(3; 1)
a) (7, 2) b) (7/2, 4/2)
a) (0; 5) b) (0; -3) c) (0; 1) c) (2, 39 d) (14/3, 4/3)
d) a y b e) a y c e) (15/3, 2/3)
http://carpetapedagogica.com/

6. 19).- Dados los puntos A(2,2) y B(5,-2),
halle en el eje de abcisas un punto “P”
de modo que el ángulo APB sea recto.
a) (1, 0) b) (6, 0) c) (5, 0)
d) (2, 0) e) a y b
20).- Dados los puntos P(2,1) y Q(8, 5).
Determinar sobre el eje de abcisas un
punto M de tal manera que la suma de
distancias hacia los puntos P y Q sea
mínima.
a) (3, 0) b) (4, 0) c) (5, 0)
d) (6,0) e) (7, 0)
http://carpetapedagogica.com/