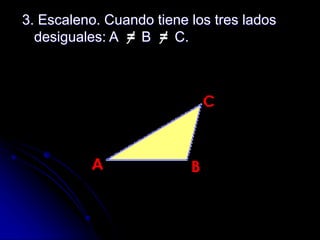
Este documento describe los diferentes tipos de triángulos clasificados por sus lados y ángulos. Explica que hay triángulos equiláteros, isósceles y escalenos dependiendo de si tienen lados iguales o desiguales, y triángulos agudos, rectángulos u obtusángulos dependiendo de si sus ángulos son agudos, rectos u obtusos. También define elementos notables de los triángulos como las alturas, mediatrices, medianas y bisectrices, y cómo se cortan para formar puntos como el ortoc

1. TRIANGULOS.

2. A Pitágoras y su escuela se debe la
demostración del teorema que lleva su
nombre sobre triángulos rectángulos.
También se atribuye la escuela pitagórica
la demostración de la propiedad de la
suma de los ángulos internos de un
triángulo y la construcción geométrica del
polígono estrellado de cinco lados.

3. Concepto y tipos de triángulos.
Triángulo es una figura cerrada, formada
por tres segmentos que, considerados dos
a dos, tienen un extremo común.
Cada uno de los
segmentos AB, BC y CA
es un lado del triánguo.

4. Atendiendo a los lados y a los
ángulos del triángulo, los
triángulos se clasifican en:

5. a). Tipos de triángulos en
relación con los lados.

6. 1. Equilátero. Cuando tiene tres lados
iguales: a = b = c.
Se cumple A=B=C ,es decir, que los tres
ángulos también son iguales.

7. 2. Isósceles. Cuando tiene dos lados iguales
y el otro desigual.
Se cumple que los ángulos A y C son
iguales: A=C.

8. 3. Escaleno. Cuando tiene los tres lados
desiguales: A B C.

9. b). Tipos de triángulos en
relación con los ángulos.

10. 1. Acutángulo. Cuando tiene los tres
ángulos agudos : A, B, C < 90º.

11. 2. Rectángulo. Cuando tiene u ángulo recto.
Los lados que forman el ángulo recto se
llaman catetos y el ángulo opuesto
hipotenusa:
A = 90º
B, C < 90º
a: hipotenusa.
b, c: catetos.

12. 3. obtusángulo. Cuando tiene un ángulo
obtuso:

13. Ahora exponemos los
elementos notables de un
triángulo:

14. Se denomina altura a cada una de las
perpendiculares trazadas desde un vértice
al lado opuesto (o su prolongación). Las
tres alturas de un triángulo se cortan en
un punto R, llamado ortocentro.

15. Mediatrices de un triángulo son las
perpendiculares trazadas a los lados del
segmento en su punto medio.
Las tres mediatrices se
cortan en un punto
llamado circuncentro,
por ser centro de una
circunferencia
circunscrita al triángulo.

16. Mediana es cada uno de los segmentos
que van desde un vértice hasta el punto
medio del lado opuesto.
Las tres medianas
se cortan en un
punto llamado
baricentro.

17. Bisectrices de un triángulo son las de los
ángulos que se forman en los vértices de
dicho triángulo.
Las tres bisectrices
se cortan en un
punto llamado
incentro, por ser
centro de una
circunferencia
inscrita en el
triángulo, es decir,
tangente a los lados
del mismo.

18. Área y Perímetro.
b: base.
h: altura.