El documento presenta un resumen de los antecedentes históricos de la trigonometría desde la civilización egipcia, babilónica y griega. Explica que la trigonometría surgió para resolver problemas astronómicos y de construcción. También define conceptos básicos como ángulo, clasificación de ángulos, y relaciones entre ángulos formados por dos rectas paralelas y una secante.































































































![SBG
Escuelas Preparatorias
Oficiales del Estado de México
Trigonometría
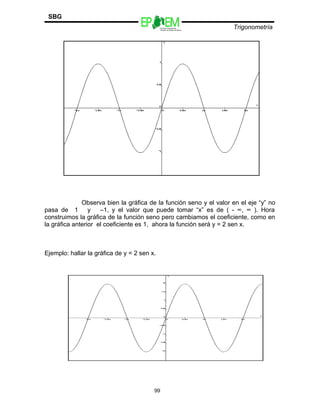
Observa que en el eje “y” el máximo y mínimo valor es de, es decir
aumento la amplitud en el eje “y” de [2,-2], y en el eje “x” es de ( - ∞, ∞ ).
Ejemplo: hallar la gráfica de y = sen 2x
Observa que el valor del ángulo “x” al duplicarlo la curva es más
continua, es decir, se hace más periódica.
Ejemplo: hallar la gráfica de y = tan x.
Observa que para la gráfica de la función tangente los valores en el
eje “y” van desde ( - ∞, ∞), en un intervalo de cada 180º, es decir en –90º y 90º el
valor da la tangente es indefinido.
100](https://image.slidesharecdn.com/trigonometria-130411204545-phpapp01/85/Trigonometria-97-320.jpg)



































