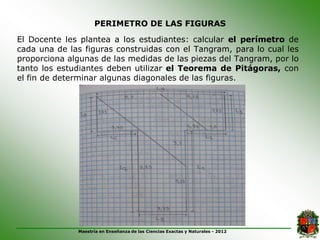
Este documento describe cómo usar el tangram, un rompecabezas chino compuesto de 7 piezas, para enseñar conceptos matemáticos como el cálculo del perímetro y la aplicación del Teorema de Pitágoras. El autor propone actividades como construir figuras geométricas y letras con el tangram, calcular perímetros usando el Teorema de Pitágoras, y concluye que el tangram permite enseñar varios conceptos matemáticos de manera lúdica y motivadora para los estudiantes.

1. Enseñanza de las Matemáticas
Haciendo Matemáticas con el Tangram
(Cálculo del perímetro y aplicación del Teorema de
Pitágoras)
Por:
Harold García Aparicio
Maestría en Enseñanza de las Ciencias Exactas
y Naturales
UNIVERSIDAD NACIONAL DE COLOMBIA
Sede Palmira
2012

2. OBJETIVO GENERAL
Fomentar el desarrollo de valores en el Aula de
Matemáticas y promover en los estudiantes el desarrollo
del pensamiento creativo en el ámbito educativo.
OBJETIVOS ESPECIFICOS
 Aprovechar las tendencias naturales de manipular objetos
concretos para, a través de la observación, el diseño, la
construcción y la composición de dichos objetos analizar
las propiedades de carácter matemático que existen en
ellos y su utilización.
 Utilizar los juegos para que los estudiantes desarrollen la
capacidad lógica del razonamiento, la observación y la
concentración, potenciando así la confianza en sus propias
capacidades y aumentando el autoestima.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

3. EL TANGRAM
El Tangram, dentro de los juegos geométricos, quizás sea el más
conocido. Existen bastantes tipos de tangram.
El tangram chino es un rompecabezas que resulta de partir un cuadrado
en siete partes, como se indica en la figura. El tangram tiene como
objetivo la composición de imágenes gráficas, tomando como base las
siete piezas invariables (en chino tangram significa "tabla de la sabiduría“)
Puede ser usado en clase de matemáticas con diferentes finalidades.
Además de figuras geométricas con el tangram, podemos construir letras,
números, animales, figuras humanas, objetos cotidianos, figuras
inventadas, y otros.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

4. CONSTRUCCION DE FIGURAS
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

5. Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

6. Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

7. Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

8. ¿Qué podemos hacer con el tangram?
Tiene un interés didáctico, ya que con él podemos trabajar:
• Reconocer las distintas figuras que lo componen.
• Reconocimiento de otras formas geométricas.
• Reconocimiento de figuras simples en una figura más compleja.
• Copiar contornos de figuras y rellenarlas con las figuras del
Tangram.
• Composición y descomposición de figuras geométricas.
• Estudio de los conceptos de paralelismo y perpendicularidad.
• Clasificación de polígonos.
• Construcción de polígonos convexos y cóncavos.
• Introducir el concepto de longitud.
• Desarrollar el concepto de perímetro de figuras planas.
• Desarrollar la noción de área.
• Estudio de polígonos con áreas iguales o perímetros iguales.
• Medir áreas, tomando como unidad el triángulo pequeño.
• Ordenar las piezas por áreas.
• Relaciones de adición y sustracción entre piezas.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

9. • Estudio de figuras con áreas equivalentes.
• Concluir que para figuras con el mismo área, tenemos
perímetros distintos.
• Introducción del concepto de amplitud.
• Comparación y ordenación de ángulos.
• Suma de ángulos interiores de un polígono.
• Suma de ángulos exteriores de un polígono.
• Estudio de fracciones
• Desarrollar la creatividad de cada alumno con la composición
de figuras libres.
Se pueden trabajar además otros conceptos:
• Comprobar el Teorema de Pitágoras
• Estudio de triángulos semejantes
• Introducción de √2
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

10. Laboratorio – Taller: “El Tangram de 4 piezas”
Dirigido a: Grados Octavos
CONCEPTOS PREVIOS
Formas, superficies y volúmenes.
Simetrías, regularidades y movimientos en las formas.
Proporción y escala.
Medidas: longitudes, áreas y volúmenes.
MATERIALES
Los materiales a utilizar serán una diversidad de rompecabezas
(de cuatro piezas) y juegos lógicos.
PROCEDIMIENTO
El Docente dibuja varias figuras en el tablero, los estudiantes
deben observarlas y familiarizarse con ellas.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

11. CONSTRUCCION DE FIGURAS
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

12. PIEZAS DEL TANGRAM
El Docente suministra un juego de Tangram a cada uno de los
grupos (conformados por 3 estudiantes). Los estudiantes
trabajan en la construcción de las diferentes figuras.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

13. DIDUJO DE LAS FIGURAS
El Docente propone a los estudiantes que realicen el
correspondiente dibujo de las figuras construidas con su
respectiva solución. Los estudiantes elaboran los dibujos de las
figuras, para lo cual deben guardar proporciones y manejar escala.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

14. PERIMETRO DE LAS FIGURAS
El Docente les plantea a los estudiantes: calcular el perímetro de
cada una de las figuras construidas con el Tangram, para lo cual les
proporciona algunas de las medidas de las piezas del Tangram, por lo
tanto los estudiantes deben utilizar el Teorema de Pitágoras, con
el fin de determinar algunas diagonales de las figuras.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

15. TEOREMA DE PITÁGORAS
El Teorema de Pitágoras establece que en un triángulo
rectángulo, el cuadrado de la hipotenusa (el lado de mayor
longitud del triángulo rectángulo) es igual a la suma de los
cuadrados de los catetos (los dos lados menores del
triángulo, los que conforman el ángulo recto).
Teorema de Pitágoras
En todo triángulo rectángulo el cuadrado de la hipotenusa es
igual a la suma de los cuadrados de los catetos.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

16. Pitágoras de Samos
Si un triángulo rectángulo tiene catetos de longitudes a y b, y la
medida de la hipotenusa es c, se establece que:
c² = a² + b²
Pitágoras ( c²=a²+b² )
Fórmulas prácticas
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

17. CONCLUSIONES
El Tangram es especialmente útil para trabajar la intuición
espacial y la imaginación; estas dos cosas intuición e imaginación
son fundamentales para el aprendizaje de la geometría.
El Tangram permite tratar gran variedad de contenidos
matemáticos: construcciones geométricas, topología, estudio de
posibilidades, combinatoria, geometría métrica (Teorema de
Pitágoras, calculo de áreas y perímetros), números racionales e
irracionales, particiones, equivalencia de figuras, etc.
Pero hay sobre todo, una cosa que destaca sobre todas las
demás: es el carácter lúdico del juego que hace que la
motivación este siempre presente y haga que los estudiantes no
se den por vencidos y persistan en la búsqueda de soluciones,
objetivo clave en las matemáticas.
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012

18. BIBLIOGRAFIA
• http://www.juegotangram.com.ar/
•http://piensoyjuego.es/index.php?module=home&func=jugar&cat=puzz
• http://es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras
• http://www.um.es/docencia/pherrero/mathis/pitagoras/teorema.htm
Maestría en Enseñanza de las Ciencias Exactas y Naturales - 2012