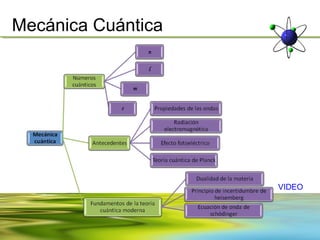
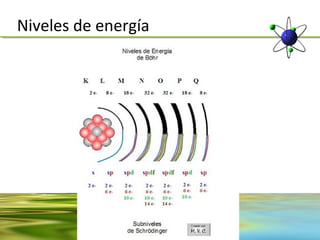
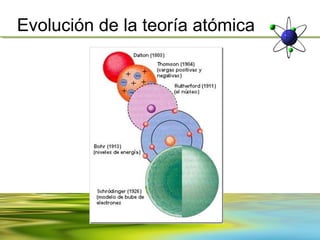
Este documento resume la evolución de la teoría atómica desde la física clásica hasta la mecánica cuántica. Explica las propiedades de las ondas y cómo científicos como Faraday, Maxwell y Planck contribuyeron al desarrollo de la teoría electromagnética y cuántica. También cubre conceptos como los niveles de energía, los números cuánticos, las formas de los orbitales atómicos y ejercicios relacionados con estos temas.

1. UNIVERSIDAD AUTONOMA DE CHIHUAHUA
FACULTAD DE INGENIERIA
QUIMICA GENERAL
2. ESTRUCTURA ATÓMICA
TITULAR: M.C DALILA ESCUDERO

2. Evolución de la teoría atómica

3. Física clásica
De la física clásica a la teoría cuántica
Los primeros intentos de los físicos del siglo XIX suponían que los
átomos se comportaban como pelotas que rebotaban
Fueron capaces de predecir y explicar algunos fenómenos
macroscópicos, como la presión que ejerce un gas
No podía explicar que fuerzas mantenían unidos a los átomos
Paso mucho tiempo para que se descubriera y se aceptara que las
propiedades de los átomos y de las moléculas no son gobernadas por
las leyes físicas que rigen a los objetos mas grandes.

4. Propiedades de las ondas
Onda: alteración vibrátil mediante la cual se trasmite la energía

5. Propiedades de las ondas

6. Propiedades de las ondas
Las propiedades características de las ondas son su longitud y altura, así como el
número de ondas que pasan por un determinado punto en un segundo
La longitud de onda (lambda); es la distancia entre puntos iguales de ondas
sucesivas
La frecuencia (nu); es el numero de ondas que pasan por un punto particular en
un segundo
La amplitud de la onda; es la distancia vertical de la línea media a la cresta o al
valle de la onda
La velocidad (u) es otra de las propiedades importantes de una onda y del medio
en el cual viaja (V.gr. Aire, agua, o vacío) y es producto de su longitud y frecuencia.

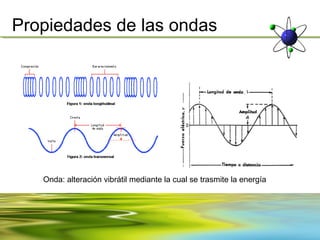
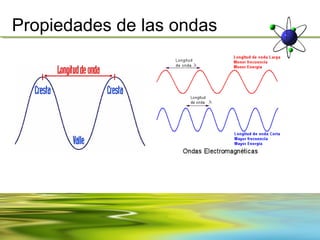
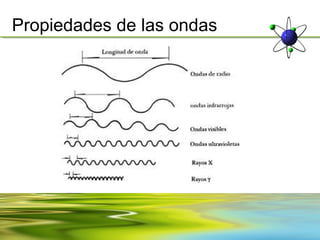
7. Propiedades de las ondas
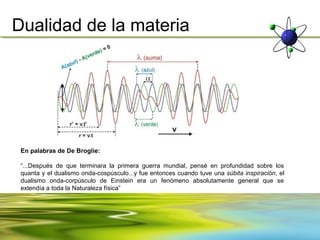
La velocidad es otra de las propiedades importantes de las ondas y del
medio en el cual viaja (por ejemplo: aire, agua o vacio) y es producto de su
longitud y frecuencia.
Distancia Distancia ondas
= =
Tiempo Onda Tiempo
v= λf
v= velocidad [m/s]
λ= longitud de onda [m]
f= frecuencia [Hz] (nu)

8. Propiedades de las ondas

9. Propiedades de las ondas
Calcule la velocidad de una onda cuya longitud de onda y
frecuencia son 17.4 cm y 87.4 Hz respectivamente
v= λf
v= (17.4)(87.4/s)
v= 1.52 x103

10. Faraday
En 1801, Michael Faraday realizó una serie de experimentos que lo llevaron a
determinar que los cambios temporales en el campo magnético inducen un
campo eléctrico. Esto se conoce como la ley de Faraday.

11. Teoría de Maxwell
Componente eléctrico en azul y el componente magnético en verde
Maxwell propuso que eso era luz

12. Radiación electromagnética
C= 3.00x108/ s en el vacio
C= 186 000 millas en el
vacio
VIDEO

13. Niveles de energía

14. Niveles de energía

15. Radiación electromagnética
Componentes del campo eléctrico y del magnético de una onda
electromagnética. Estos dos componentes tienen la misma longitud de onda,
frecuencia y amplitud pero cada uno viaja en un plano perpendicular al del otro

16. Radiación electromagnetica

17. Radiación electreomagnetica

18. Radiación electromagnética

19. Radiación electromagnética
La longitud de onda de la luz verde de un semáforo esta alrededor
de 522nm ¿Cual es la frecuencia de esta radiación?

20. El efecto fotoeléctrico

21. Teoría cuántica de Planck
En 1900 con el joven alemán Max Planck
Físico que al examinar los datos de la radiación que emitían los sólidos
calentados a diferentes temperaturas descubrió que los átomos y las
moléculas emitían energía solo en cantidades discretas o cuanta.

22. Teoría cuántica de Planck

23. Teoría cuántica de Planck

24. Teoría cuántica de Planck
Calcule la energía en joules de:
a) un fotón con una lambda de 5.00 x104 nm (región infrarroja)
b) Un fotón que tiene una longitud de onda de 5.00x10-2 nm (región de
rayos X)

25. Dualidad de la materia

26. Dualidad de la materia
En palabras de De Broglie:
“...Después de que terminara la primera guerra mundial, pensé en profundidad sobre los
quanta y el dualismo onda-cospúsculo...y fue entonces cuando tuve una súbita inspiración, el
dualismo onda-corpúsculo de Einstein era un fenómeno absolutamente general que se
extendía a toda la Naturaleza física”

27. Principio de incertidumbre de hieisemberg

28. Ecuación de Onda de Schödinger
Uno de los primeros desarrollos de la mecánica cuántica fué
llevado a cabo por Erwin Schrödinger en 1925 al deducir la
ecuación que obedece la función de onda asociada con una
partícula.

29. Mecánica Cuántica
VIDEO

30. Estructura atómica

31. Niveles de energía

32. Niveles de energía

33. Niveles de energía

34. Números Cuanticos
Numero Nombre Valores Ejemplos Se relaciona con Indica Establecido
cuantico permitidos de valores por
n
Numero Enteros 1,2,3…7 Espacio Nivel Bohr
cuantico Positivos energético
principal
l
Numero Desde cero 0,1,2,3... Con la forma del Subnivel o Somerfield
cuantico hasta orbital tipo de
secundario n-1 orbital
m
Numero Desde -l hasta -1,0,1 La orientacion de El numero De Broglie,
Cuantico + l, pasando un orbital de orbitales Heisenberg
magnetico por cero
s
Numero +1/2, -1/2 La posibilidad de Giro del Schrodinger
cuantico que un orbital electrón
espin acepte o no un
orbital

35. Ley de Rydberg
Se usa para determinar el número de electrones por
nivel, cuya expresión es:
Número de electrones= 2n^2
1er Nivel 2do Nivel  3er Nivel 4to Nivel
K (n=1) L (n=2) M (n=3) N (n=4)
2(1)^2=2 2 (2)^2=8 2(3)^2= 18 2(4)^2= 32

36. Calculo de e- por subnivel
El número de Electrones por subnivel se determina de la siguiente
forma: 2 (2 (l )+1 = No. De e− por Subnivel.
Valor Fórmula 2(2(l )+1) e- por
de l Subnivel
l=0 2(2(0)+1)= 2(0+1)= 2(1) 2
l=1 2(2(1)+1)= 2(2+1) = 2(3) 6
l=2 2(2(2)+1)= 2(4+1) = 2(5) 10
l=3 2(2(3)+1)= 2(6+1) = 2(7) 14

37. Tipos de Orbitales
Tipo de Forma Valores de l Número Valores de m Número
orbitales de formas de e-
Esférica 0 1 0 2
s
cacahuate 1 3 -1,0,1 6
p
indefinida 2 5 -2,-1,0,1,2 10
d
indefinida 3 7 -3,-2,-1,0,1,2,3 14
f

38. Función de onda angular

39. Formas de los orbitales

40. Formas de los orbitales

41. Orbitales s
Representación de la parte angular de la función de onda de los orbitales s
(probabilidad 75 %)

42. Orbitales p
Representación de la parte angular de la función de onda de los orbitales p
(probabilidad 75 %)

43. Orbitales d
Representación de la parte angular de
la función de onda de los orbitales d
(probabilidad 75 %).

44. Orbitales f
Representación de la parte angular de la función de onda de los orbitales f (probabilidad 75 %)

45. Niveles de energía

46. Ejercicios de Números cuanticos
1. Indicar los posibles valores de l,m y s
a) n=2 l= 0,+1 (2 valores) m= 0,-1,0,+1 (4 valores)
s= ½,-½, ½,-½, ½,-½, ½,-½ (8 valores)
b) n=3
l = 0,1,2 (3 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2 (9 valores)
s= ½,-½, ½,-½, ½,-½, ½,-½,½,-½, ½,-½, ½,-½, ½,-½, ½,-½ (18 valores)
c) n = 1 l =0 (1 valor), m =0 (1 valor), s= ½,-½ (2 valores)
d) Indique si n puede tener valores negativos NO

47. Ejercicios de Números cuanticos
2. Calcule los valores de l y m y diga cual es el numero total de orbitales
asociados con
a) n=3 9 ORBITALES l = 0,1,2 (3 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2 (9 valores)
b) n=5 25 ORBITALES l = 0,1,2,3,4 (5 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2,-3,-2,-
1,0,1,2,3,-4,-3,-2,-1,0,1,2,3,4 (25 valores)
c)n=2 4 ORBITALES l= 0,+1 (2 valores) m= 0,-1,0,+1 (4 valores)
d)n=4 16 ORBITALES l = 0,1,2,3, (4 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2,-3,-2,-
1,0,1,2,3 (16 valores)
e) n = 1 1 ORBITAL l =0 (1 valor), m =0 (1 valor)

48. Ejercicios de Números cuanticos
3. Un electrón de cierto átomo esta en el nivel cuántico que se indica…
escriba los posibles valores de l y m
a) n=2 l= 0,+1 (2 valores) m= 0,-1,0,+1 (4 valores)
b) n=3 l = 0,1,2 (3 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2 (9 valores)
d) n=4 l = 0,1,2,3, (4 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2,-3,-2,-1,0,1,2,3 (16 valores)
e) n=5 l = 0,1,2,3,4 (5 valores) m = 0,-1,0,+1,-2,-1,0,+1,+2,-3,-2,-1,0,1,2,3,-4,-3,-2,-
1,0,1,2,3,4 (25 valores)

49. Ejercicios de Números cuanticos
4. De los valores de los números cuanticos para los siguientes electrones
a) 2p b) 3s c) 5d d) 3p e) 4d
(3,0,0,½), (5,2,-2, ½), (4,2,-2,½),
(2,1,-1, ½), (3,1,-1,½),
(3,0,0,-½) (5,2,-2,-½), (4,2,-2,-½),
(2,1,-1,-½), (3,1,-1,-½),
(5,2,-1, ½), (4,2,-1,½),
(2,1, 0, ½), (3,1, 0, ½),
(5,2,-1,-½), (4,2,-1,-½),
(2,1, 0,-½), (3,1, 0,-½),
(5,2, 0, ½), (4,2,0,½),
(2,1, 1, ½), (3,1, 1, ½),
(5,2, 0,-½), (4,2,0,-½),
(2,1, 1,-½) (3,1, 1,-½)
(5,2, 1, ½), (4,2,-1,½),
(5,2, 1,-½), (4,2,1,-½),
(5,2, 2, ½), (4,2,2,½),
(5,2, 2,-½) (4,2,2,-½)

50. Ejercicios de Números cuanticos
5. Calcule el numero total e electrones que puede ocupar
a) Un orbital s
2e−
b) Tres orbitales p
6e−
c) Cinco orbitales d
10e−
d) Siete orbitales f
14e−

51. Ejercicios de Números cuanticos
6. Cual es el numero máximo de electrones que puede ocupar cada
uno de los siguientes subniveles…
a) 3s 2e−
b) 3d 10e−
c) 4p 6e−
d) 4f 14e−
e) 5f 14e−

52. Ejercicios de Números cuanticos
7. Exprese las diferentes formas en que se pueden escribir los cuatro numeros
cuánticos que identifican un orbital 3p
3p
(3,1,-1,½),
(3,1,-1,-½),
(3,1, 0, ½),
(3,1, 0,-½),
(3,1, 1, ½),
(3,1, 1,-½)

53. Fundamentos del primer láser
VIDEO

54. Fundamentos del primer láser
VIDEO

55. GRACIAS!!!