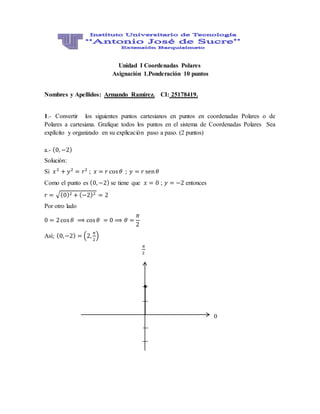
Este documento contiene la resolución de varios ejercicios relacionados con la conversión entre coordenadas cartesianas y polares. El estudiante convierte puntos entre ambos sistemas de coordenadas y resuelve ecuaciones transformándolas de cartesianas a polares. También determina puntos comunes entre curvas y calcula áreas relacionadas con funciones dadas en coordenadas polares.

1. Unidad I Coordenadas Polares
Asignación 1.Ponderación 10 puntos
Nombres y Apellidos: Armando Ramírez. CI: 25178419.
1.- Convertir los siguientes puntos cartesianos en puntos en coordenadas Polares o de
Polares a cartesiana. Grafique todos los puntos en el sistema de Coordenadas Polares Sea
explícito y organizado en su explicación paso a paso. (2 puntos)
a.- (0, −2)
Solución:
Si 𝑥2
+ 𝑦2
= 𝑟2
; 𝑥 = 𝑟 cos 𝜃 ; 𝑦 = 𝑟 sen 𝜃
Como el punto es (0, −2) se tiene que 𝑥 = 0 ; 𝑦 = −2 entonces
𝑟 = √(0)2 + (−2)2 = 2
Por otro lado
0 = 2cos 𝜃 ⟹ cos 𝜃 = 0 ⟹ 𝜃 =
𝜋
2
Así; (0,−2) = (2,
𝜋
2
)
𝜋
2
0

2. b.- (1, √3)
Solución:
Si 𝑥2
+ 𝑦2
= 𝑟2
; 𝑥 = 𝑟 cos 𝜃 ; 𝑦 = 𝑟 sen 𝜃
Como el punto es (1, √3)se tiene que 𝑥 = 1 ; 𝑦 = √3 entonces
𝑟 = √(1)2 + (√3)
2
= 2
Por otro lado
√3 = tan 𝜃 ⟹ 𝜃 = tan−1
(√3) ⟹ 𝜃 =
𝜋
3
Así; (1, √3) = (2,
𝜋
3
)
𝜋
2
𝜋
3
𝜋 0
c.- (2,0)
Solución:
Si 𝑥 = 2 ; 𝑦 = 0 entonces
𝑟 = √(2)2 + (0)2 = 2
Además;
0 = 2sen 𝜃 ⟹ sen 𝜃 = 0 ⟹ 𝜃 = 𝜋
Por tanto (2,0) = (2, 𝜋)

3. 𝜋
2
𝜋 0
d.- (1, −2)
Aquí tenemos que 𝑥 = 1 ; 𝑦 = −2 entonces
𝑟 = √(1)2 + (−2)2 = √5
Ahora
−
2
1
= tan 𝜃 ⟹ 𝜃 = tan−1(−2) ⟹ 𝜃 = 180° − 63,4 = 116,6
Así; (1,−2) = (√5,116,6°)
𝜋
2
116,6°
𝜋 0

4. e.- (1,240º)
En este caso 𝑟 = 1 ; 𝜃 = 240° = 240°
1𝜋
180°
=
4𝜋
3
entonces
𝑥 = 1cos(
4𝜋
3
) = −
1
2
𝑦 = 1 sen(
4𝜋
3
) =−
√3
2
Por tanto (1,240°) = (−
1
2
, −
√3
2
)
𝜋
2
𝜋 0
(1,240°)
3𝜋
2

5. f.- (4,
𝜋
2
)
Tenemos que 𝑟 = 4 ; 𝜃 =
𝜋
2
por tanto;
𝑥 = 4 cos(
𝜋
2
) = 4(0) = 0
𝑦 = 4 sen(
𝜋
2
) =4(1) = 4
En consecuencia (4,
𝜋
2
) = (0,4)
𝜋
2
(4,
𝜋
2
)
𝜋 0
3𝜋
2
g.- (−6,
𝜋
3
)
Solución: aquí 𝑟 = 6 𝑦 𝜃 =
𝜋
2
, por lo que
𝑥 = 6 cos(
𝜋
3
) = 6(
1
2
) = 3
𝑦 = 6 sen(
𝜋
3
) =6 (
√3
2
) = 3√3
En Consecuencia; (−6,
𝜋
3
) = (3,3√3)

6. h.- (-3,360º)
Solución: aquí 𝑟 = 3 𝑦 𝜃 = 360° = 2𝜋 de donde
𝑥 = 3 cos(2𝜋) = 3(1) = 3
𝑦 = 3 sen(2𝜋) =3(0) = 0
Así; (−3,360°) = (3,0)
𝜋
2
(−3,360°)
𝜋 0
3𝜋
2
2.- Transforme las siguientes ecuaciones: (recuerde explicar paso a paso la solución de cada
transformación) (2 puntos)
a.- yx2 – 2x = 5y2
Solución:
Considerando 𝑥 = 𝑟cos 𝜃 ; 𝑦 = 𝑟sen 𝜃 y sustituyendo en la ecuación dada obtenemos
( 𝑟 sen 𝜃)( 𝑟cos 𝜃 )2
− 2 𝑟cos 𝜃 = 5( 𝑟 sen 𝜃)2
𝑟 sen 𝜃 𝑟2
cos2
𝜃 − 2 𝑟 cos 𝜃 =5𝑟2
sen2
𝜃
𝑟3
sen 𝜃 cos2
𝜃 − 2𝑟cos 𝜃 =5𝑟2
sen2
𝜃
𝑟3
sen 𝜃 cos2
𝜃 − 5𝑟2
sen2
𝜃 − 2𝑟cos 𝜃 = 0
𝑟( 𝑟2
sen 𝜃 cos2
𝜃 − 5𝑟sen2
𝜃 − 2cos 𝜃 ) = 0 Factor Común
𝑟 = 0 v 𝑟2
sen 𝜃 cos2
𝜃 − 5𝑟sen2
𝜃 − 2cos 𝜃 = 0

7. Usando resolvente cuadrática
𝑟 =
−(−5sen2
𝜃) ± √(−5sen2 𝜃)2 − 4(sen 𝜃 cos2 𝜃)(−2cos 𝜃 )
2(sen 𝜃 cos2 𝜃)
𝑟 =
5sen2
𝜃 ± √25sen4 𝜃 + 4sen 𝜃 cos3 𝜃
2sen 𝜃 cos2 𝜃
b.- y 2x2 – x = − 3
Solución:
( 𝑟 sen 𝜃 )2( 𝑟cos 𝜃 )2
− 𝑟cos 𝜃 = 3
𝑟2
cos2
𝜃 𝑟2
sen2
𝜃 − 𝑟 cos 𝜃 = 3
𝑟4
cos2
𝜃 sen2
𝜃 − 𝑟 cos 𝜃 = 3 , No es posible simplificar aún más
c.- r = 4 cos2 𝜃
Solución:
Por ángulos dobles se tiene que cos2 𝜃 = 2cos2
𝜃 − 1 , entonces al sustituir en la ecuación
obtenemos r = 4 (2cos2
𝜃 − 1 ) ⟹ 𝑟 = 8cos2
𝜃 − 4
Ahora; si multiplicamos en ambos lados por 𝑟2
de la ecuación dada, no queda
𝑟3
= 𝑟2(8𝑟2
cos2
𝜃 − 4) ⟹ 𝑟3
= 8𝑟2
cos2
𝜃 − 4𝑟2
⟹ (√𝑥2 + 𝑦2)
3
= 8𝑥2
− 4(√𝑥2 + 𝑦2)
2
⟹ (√𝑥2 + 𝑦2)
3
= 8𝑥2
− 4( 𝑥2
+ 𝑦2)
⟹ √( 𝑥2 + 𝑦2)3 = 8𝑥2
− 4𝑥2
− 4𝑦2
⟹ √( 𝑥2 + 𝑦2)3 = 4𝑥2
− 4𝑦2
d.- r = 3 ( 1 + sin 𝜃)
Solución: si multiplicamos por 𝑟 en ambos lados de la ecuación , no queda
𝑟2
= 3𝑟(1 + 𝑠𝑒𝑛𝜃) ⟹ 𝑟2
= 3𝑟 + 3𝑟𝑠𝑒𝑛𝜃
Ahora; sustituyendo los cambios respectivos obtenemos
𝑟2
= 3𝑟 + 3𝑟𝑠𝑒𝑛𝜃 ⟹ 𝑥2
+ 𝑦2
= 3√𝑥2 + 𝑦2 + 3𝑦
⟹ 𝑥2
+ 𝑦2
− 3𝑦 = 3√𝑥2 + 𝑦2

8. 3.-
(2 puntos)
Solución:
Determinemos los puntos comunes entre las curvas;
3cos 𝜃 = 1 + cos 𝜃
3cos 𝜃 − cos 𝜃 = 1
2cos 𝜃 = 1
Cos 𝜃 = 1/2
𝜃 =
𝜋
3
Determinemos el área del cardiode
𝐴1 =
1
2
∫ (1 + cos 𝜃 )2
𝜋
3
0
𝑑𝜃
=
1
2
∫ (1 + 2 cos 𝜃 + cos2
𝜃)
𝜋
3
0
𝑑𝜃
=
1
2
∫ (1 + 2 cos 𝜃 +
1
2
+
1
2
cos2 𝜃)
𝜋
3
0
𝑑𝜃
=
1
2
∫ (
3
2
+ 2 cos 𝜃 +
1
2
cos2 𝜃)
𝜋
3
0
𝑑𝜃
=
1
2
[
3
2
𝜃 − 2𝑠𝑒𝑛𝜃 −
1
4
sen2 𝜃]
0
𝜋
3
=
𝜋
4
+
9√3
16

9. Determinemos el área del círculo
𝐴2 =
1
2
∫ (3 cos 𝜃 )2
𝜋
2
𝜋
3
𝑑𝜃
=
1
2
∫ 9cos2
𝜃
𝜋
2
𝜋
3
𝑑𝜃
=
9
2
∫ cos2
𝜃
𝜋
2
𝜋
3
𝑑𝜃
=
9
2
∫ (
1
2
+
1
2
cos2 𝜃)
𝜋
2
𝜋
3
𝑑𝜃
=
9
4
∫ (1 + cos2𝜃)
𝜋
2
𝜋
3
𝑑𝜃 =
9
4
[𝜃 −
1
2
𝑠𝑒𝑛2𝜃] 𝜋
3
𝜋
2
=
3𝜋
8
−
9√3
16
Debemos determinar el área del cardiode pero 0 ≤ 𝜃 ≤ 𝜋
𝐴3 =
1
2
∫ (
3
2
+ 2cos 𝜃 +
1
2
cos2 𝜃)
𝜋
0
𝑑𝜃
=
1
2
[
3
2
𝜃 − 2𝑠𝑒𝑛𝜃 −
1
4
sen2 𝜃]
0
𝜋
=
1
2
[
3𝜋
2
]
=
3𝜋
4
Finalmente el área que nos exigen y considerando simetría
𝐴 = 2𝐴3 − 2𝐴2 − 2𝐴1 = 2 [
3𝜋
4
−
3𝜋
8
+
9√3
16
−
𝜋
4
−
9√3
16
] = 2[
𝜋
8
] =
𝜋
4
3.- -
(2 puntos)
4.-
(2 puntos )