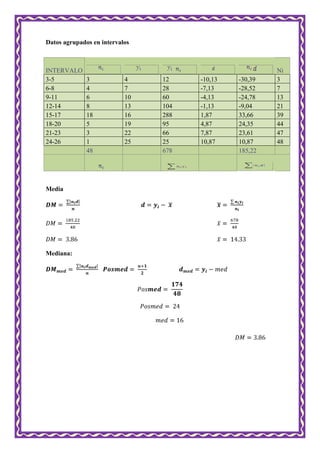
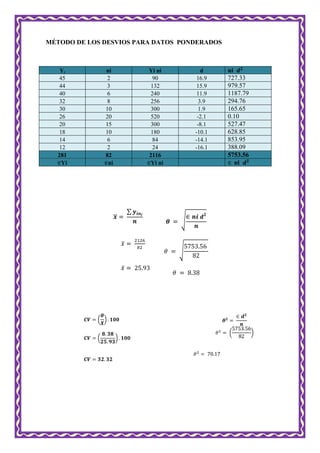
El documento habla sobre población y muestra en estadística. Define población como un conjunto finito o infinito de personas u objetos con características comunes. La muestra es una parte representativa de la población que se estudia para sacar conclusiones sobre ella. Existen muestreos probabilísticos y no probabilísticos, siendo los primeros más rigurosos científicamente porque todos los individuos tienen probabilidad positiva de ser seleccionados. También describe medidas de dispersión como desviación media y desviación típica.

1. UNIDAD IV
POBLACION Y MUESTRA
POBLACION:
El concepto de población en estadística va más allá de lo que comúnmente se conoce
como tal. Una población se precisa como un conjunto finito o infinito de personas u
objetos que presentan características comunes.
Destacamos algunas definiciones:
"Una población es un conjunto de todos los elementos que estamos estudiando, acerca
de los cuales intentamos sacar conclusiones". Levin&Rubin (1996).
"Una población es un conjunto de elementos que presentan una característica común".
Cadenas (1974).
El tamaño que tiene una población es un factor de suma importancia en el proceso de
investigación estadística y en nuestro caso social, y este tamaño vienen dado por el
número de elementos que constituyen la población, según el número de elementos la
población puede ser finita o infinita. Cuando el número de elementos que integra la
población es muy grande, se puede considerar a esta como una población infinita, por
ejemplo; el conjunto de todos los números positivos.
MUESTRA:
La muestra es una representación significativa de las características de una población,
que bajo, la asunción de un error (generalmente no superior al 5%) estudiamos las
características de un conjunto poblacional mucho menor que la población global.
"Se llama muestra a una parte de la población a estudiar que sirve para representarla".
Murria R. Spiegel (1991).
"Una muestra es una colección de algunos elementos de la población, pero no de todos".
Levin&Rubin (1996).
"Una muestra debe ser definida en base de la población determinada, y las conclusiones
que se obtengan de dicha muestra solo podrán referirse a la población en referencia",
Cadenas (1974).
Muestreo no probabilístico: En este tipo de muestreo, puede haber clara influencia de
la persona o personas que seleccionan la muestra o simplemente se realiza atendiendo a
razones de comodidad. Salvo en situaciones muy concretas, en la que los errores
cometidos no son grandes, debido a la homogeneidad de la población, en general no es
un tipo de muestreo riguroso y científico, dado que no todos los elementos de la
población pueden formar parte de la muestra. Por ejemplo, si hacemos una encuesta

2. telefónica por la mañana, las personas que no tienen teléfono o que están trabajando, no
podrán formar parte de la muestra.
Muestreo probabilístico: En este tipo de muestreo, todos los individuos de la
población pueden formar parte de la muestra, tienen probabilidad positiva de formar
parte de la muestra. Por lo tanto es el tipo de muestreo que deberemos utilizar en
nuestras investigaciones, por ser el riguroso y científico.
En el contexto de muestreo probabilístico, existen varias posibilidades de obtención de
una muestra:
Muestreo aleatorio simple
Muestreo aleatorio estratificado.
Muestreo aleatorio simple
En un muestreo aleatorio simple todos los individuos tienen la misma probabilidad de
ser seleccionados. La selección de la muestra puede realizarse a través de cualquier
mecanismo probabilístico en el que todos los elementos tengan las mismas opciones de
salir.
Muestreo aleatorio estratificado
Es frecuente que cuando se realiza un estudio interese estudiar una serie de
subpoblaciones (estratos) en la población, siendo importante que en la muestra haya
representación de todos y cada uno de los estratos considerados. El muestreo aleatorio
simple no nos garantiza que tal cosa ocurra. Para evitar esto, se saca una muestra de
cada uno de los estratos.
MEDIDAS DE DISPERCION
Al igual que sucede con cualquier conjunto de datos, la media, la
mediana y la moda sólo nos revelan una parte de la información que
necesitamos acerca de las características de los datos. Para aumentar
nuestro entendimiento del patrón de los datos, debemos medir
también su dispersión, extensión o variabilidad.
DESVIACION
MEDIA
DESVIACION
TIPICA

3. Formulas
PQ = contante de variación
N= Tamaño de la población
E = Error



MEDIDADS DE DISPERCIÓN
Las medidas de dispersión permiten determinar como se encuentra distribuidos los
valores de los cuantiles. Ya que lo más importante en este tema es la desviación media y
la desviación típica.

4. MEDIDAS
DE
DISPERCIÓN

5. MEDIDADS DE DISPERCIÓN
DESVIACIÓN MEDIA
DESVIACIÓN MEDIA.- Es el promedio de los valores absolutos de los desvíos
obtenidos desde la media-mediana-moda
DATOS SIMPLES.-
20 7,08 6
19 6,08 5
18 5,08 4
17 4,08 3
16 3,08 2
15 2,08 1
13 0,08 -1
10 -2,92 -4
8 -4,92 -6
6 -6,92 -8
4 -8,92 -10
152 55,16 55
∑|d|
Media:
Mediana:
Moda: En este caso no tenemos moda

6. Datos ponderados
Media
Mediana:
Ni
20 2 40 5,64 11,28 87 5 10
19 3 57 4,64 13,92 85 4 12
18 6 108 3,64 21,84 82 3 18
17 10 170 2,64 26,4 76 2 20
16 18 288 1,64 29,52 66 1 18
15 20 300 0,64 12,8 48 0 0
13 10 130 -1,36 -13,6 28 -2 -20
10 8 80 -4,36 -34,88 18 -5 -40
9 4 36 -5,36 -21,44 10 -6 -24
6 3 18 -8,36 -25,08 6 -9 -27
6 2 12 -8,36 -16,72 3 -9 -18
4 1 4 -10,36 -10,36 1 -11 -11
153 1243 231,84 212

7. Datos agrupados en intervalos
Media
Mediana:
INTERVALO Ni
3-5 3 4 12 -10,13 -30,39 3
6-8 4 7 28 -7,13 -28,52 7
9-11 6 10 60 -4,13 -24,78 13
12-14 8 13 104 -1,13 -9,04 21
15-17 18 16 288 1,87 33,66 39
18-20 5 19 95 4,87 24,35 44
21-23 3 22 66 7,87 23,61 47
24-26 1 25 25 10,87 10,87 48
48 678 185,22

8. DESVIACION TIPICA
MÉTODO DE LOS DESVIOS PARA DATOS SIMPLES
Yi d
45 16.9 285.61
44 15.9 252.81
40 11.9 141.61
32 3.9 15.21
30 1.9 3.61
26 -2.1 4.41
20 -8.1 65.61
18 -10.1 102.01
14 -14.1 198.81
12 -16.1 259.90
281 1328.9
Yi 

9. MÉTODO DE LOS DESVIOS PARA DATOS PONDERADOS
Yi ni Yi ni d ni
45 2 90 16.9 727.33
44 3 132 15.9 979.57
40 6 240 11.9 1187.79
32 8 256 3.9 294.76
30 10 300 1.9 165.65
26 20 520 -2.1 0.10
20 15 300 -8.1 527.47
18 10 180 -10.1 628.85
14 6 84 -14.1 853.95
12 2 24 -16.1 388.09
281 82 2116 5753.56
Yi ni Yi ni ni

10. MÉTODO DIRECTO PARA DATOS SIMPLES
Yi
45 2025
44 1936
40 1764
32 1600
30 1024
26 900
20 676
18 400
14 324
12 196
281 9225
Yi