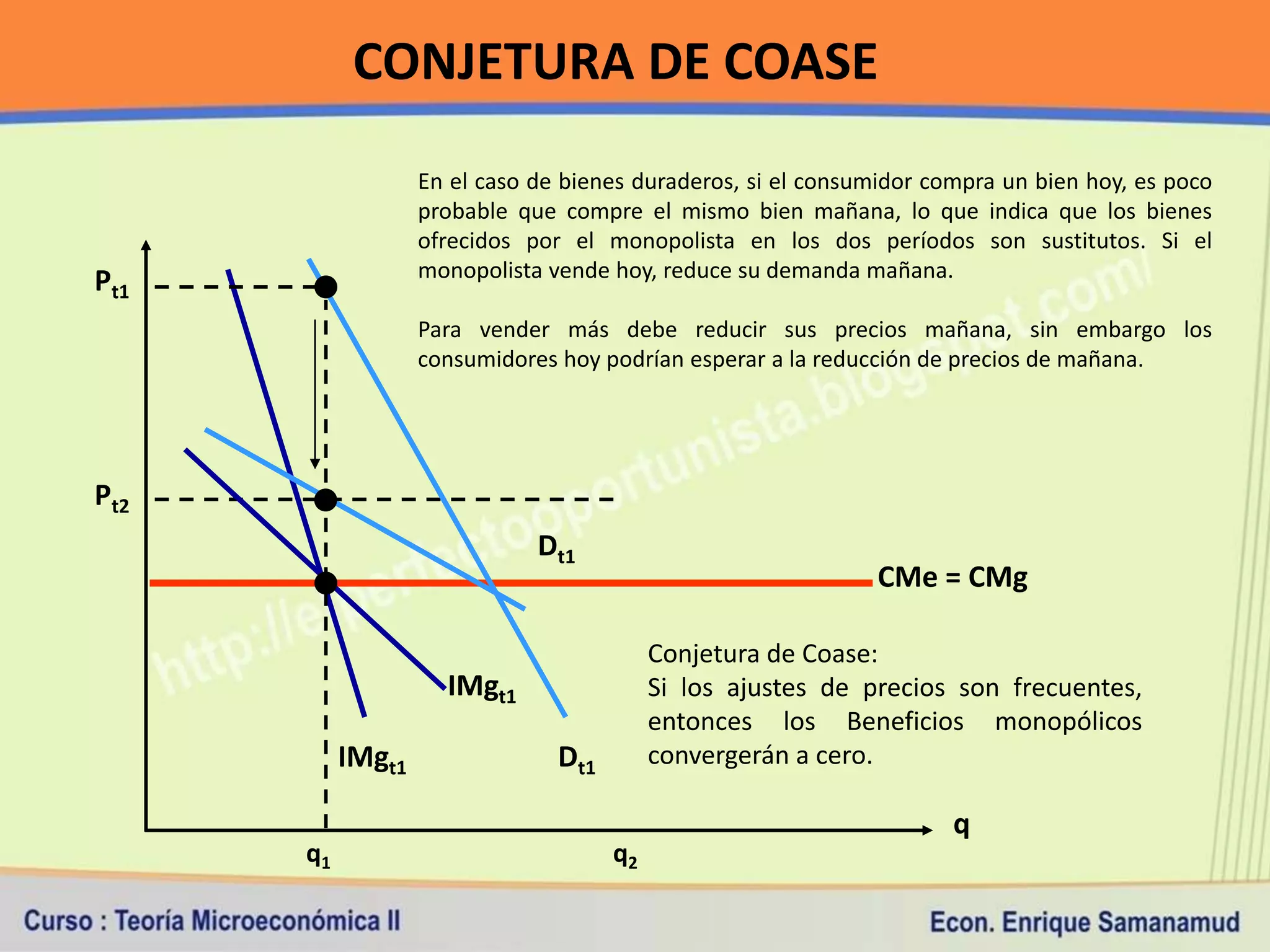
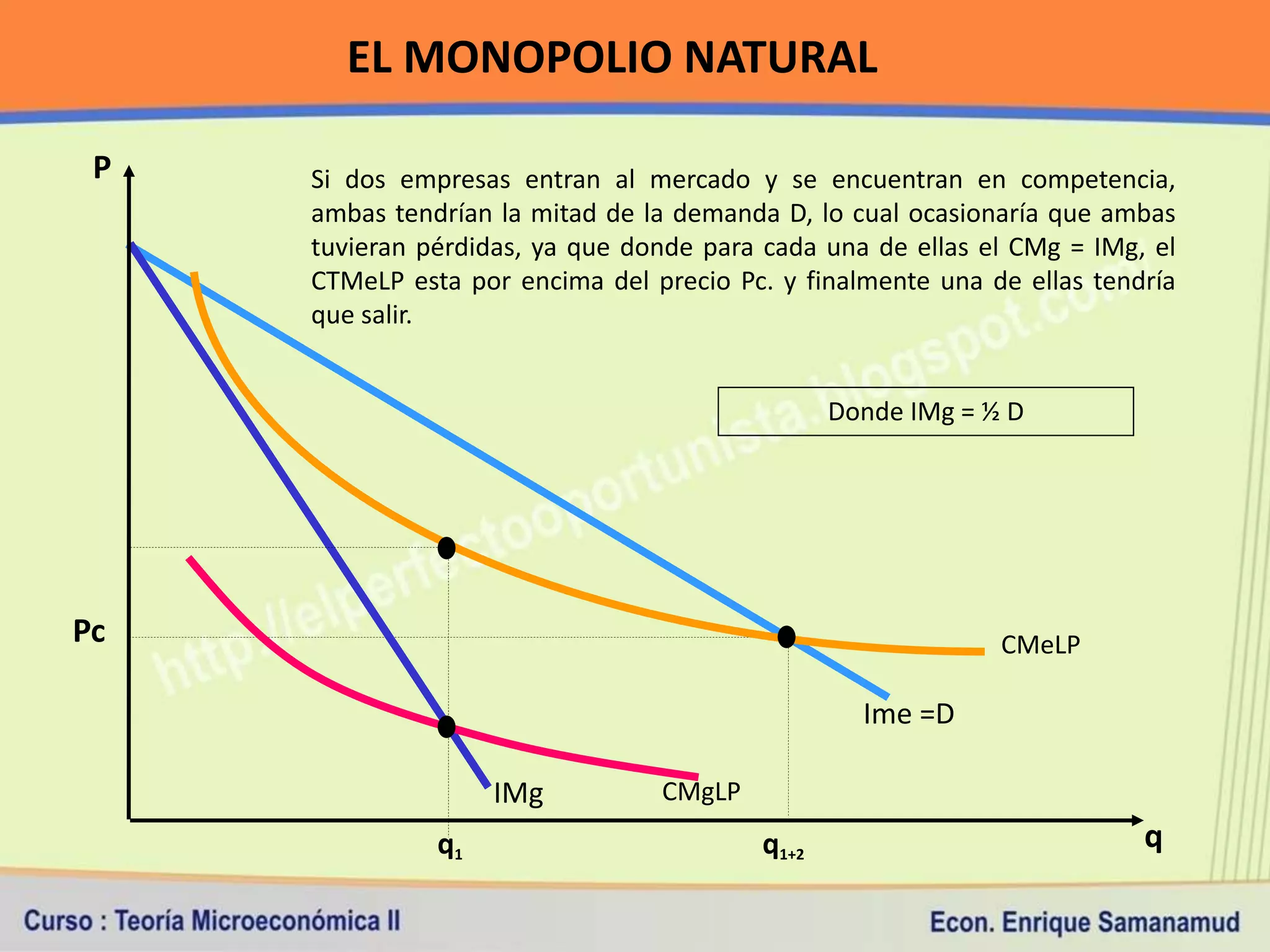
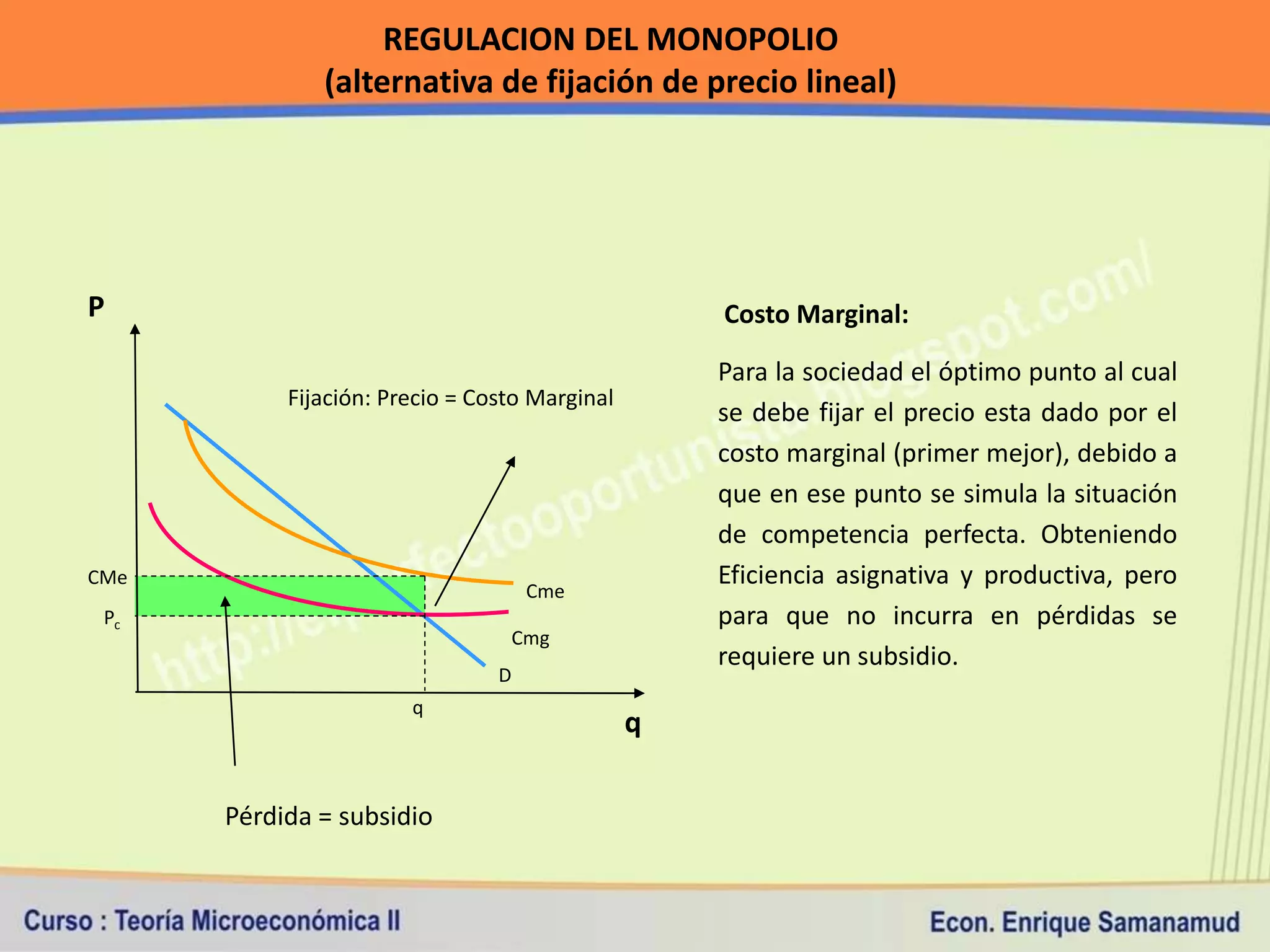
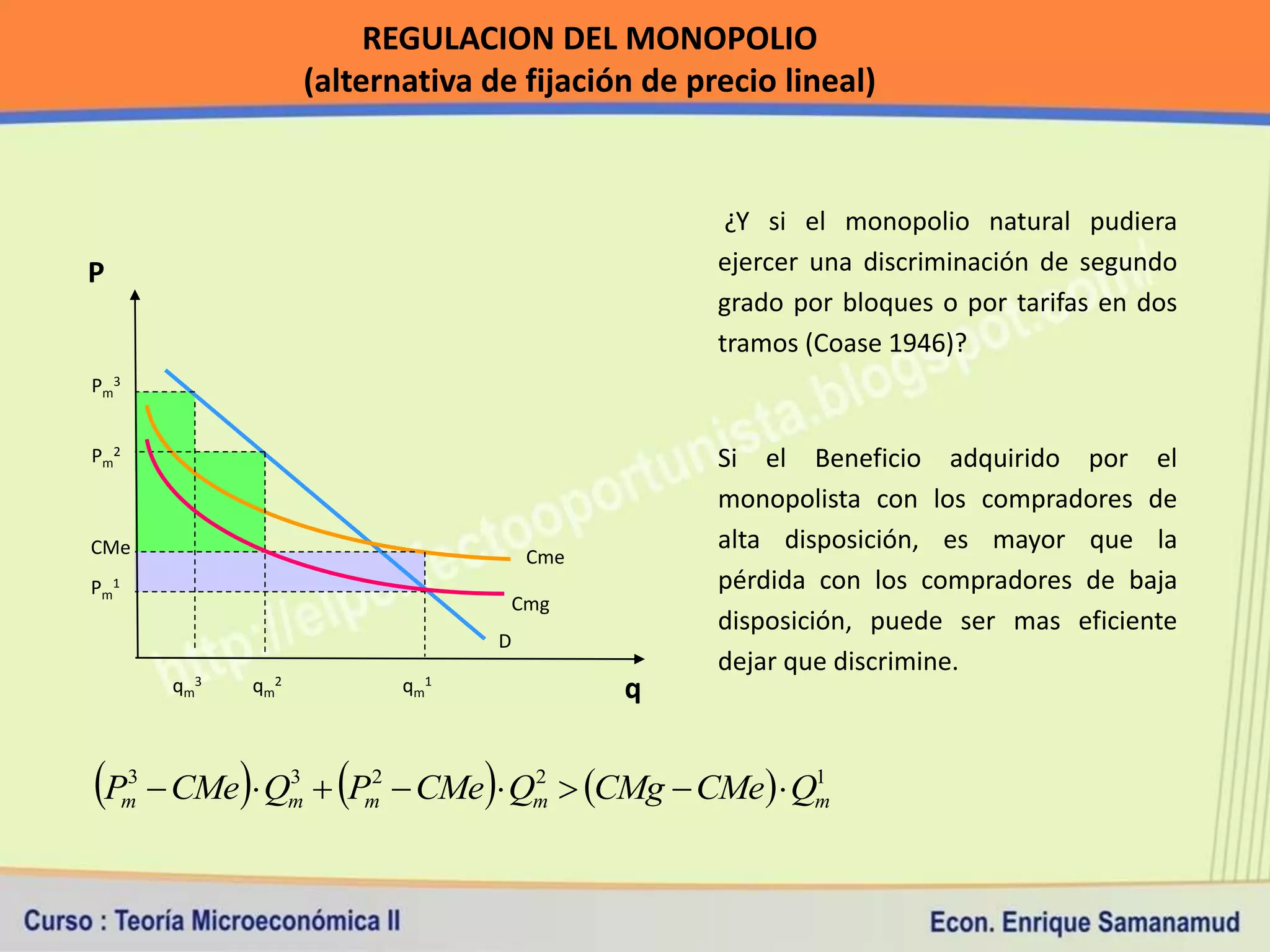
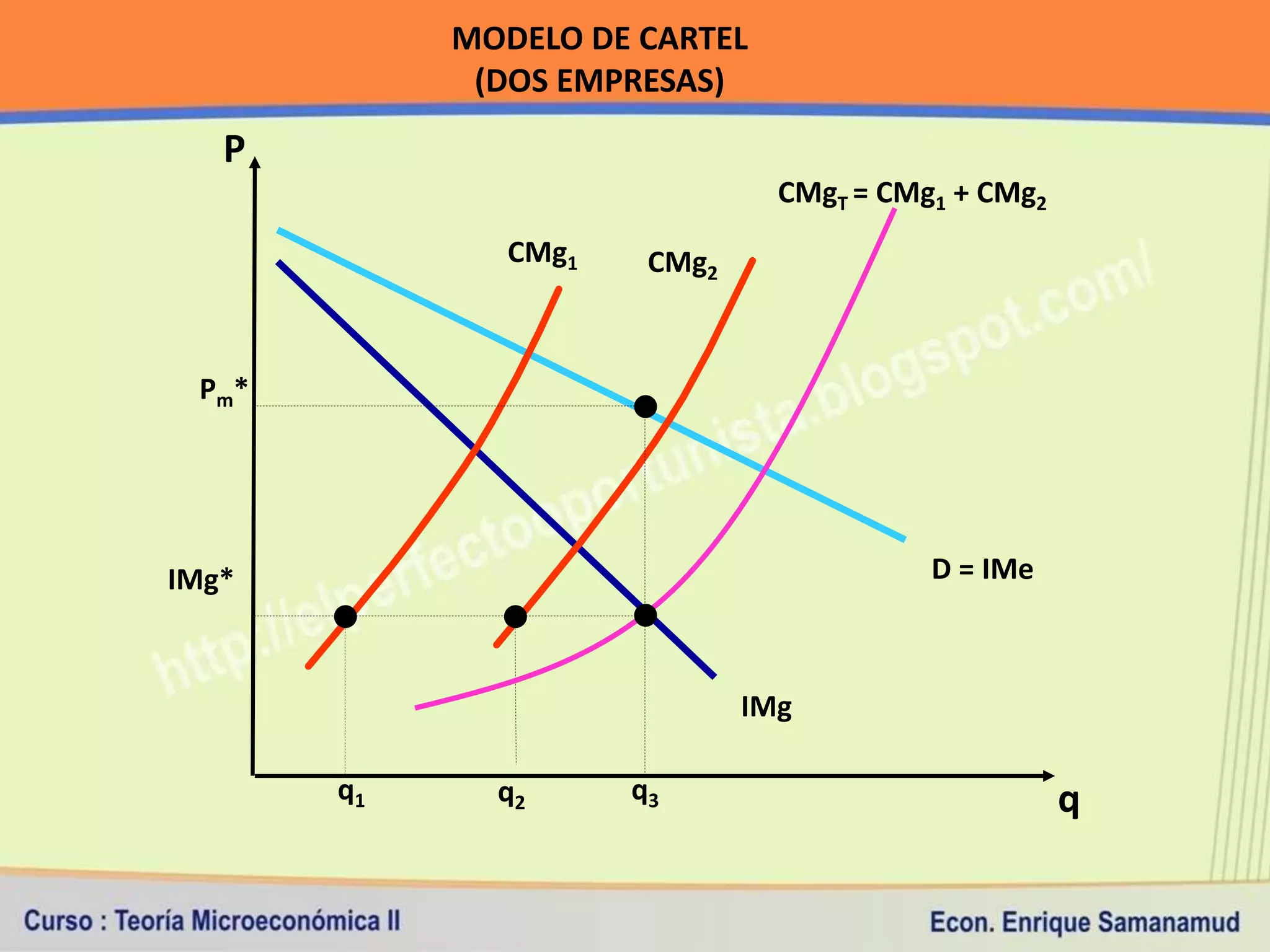
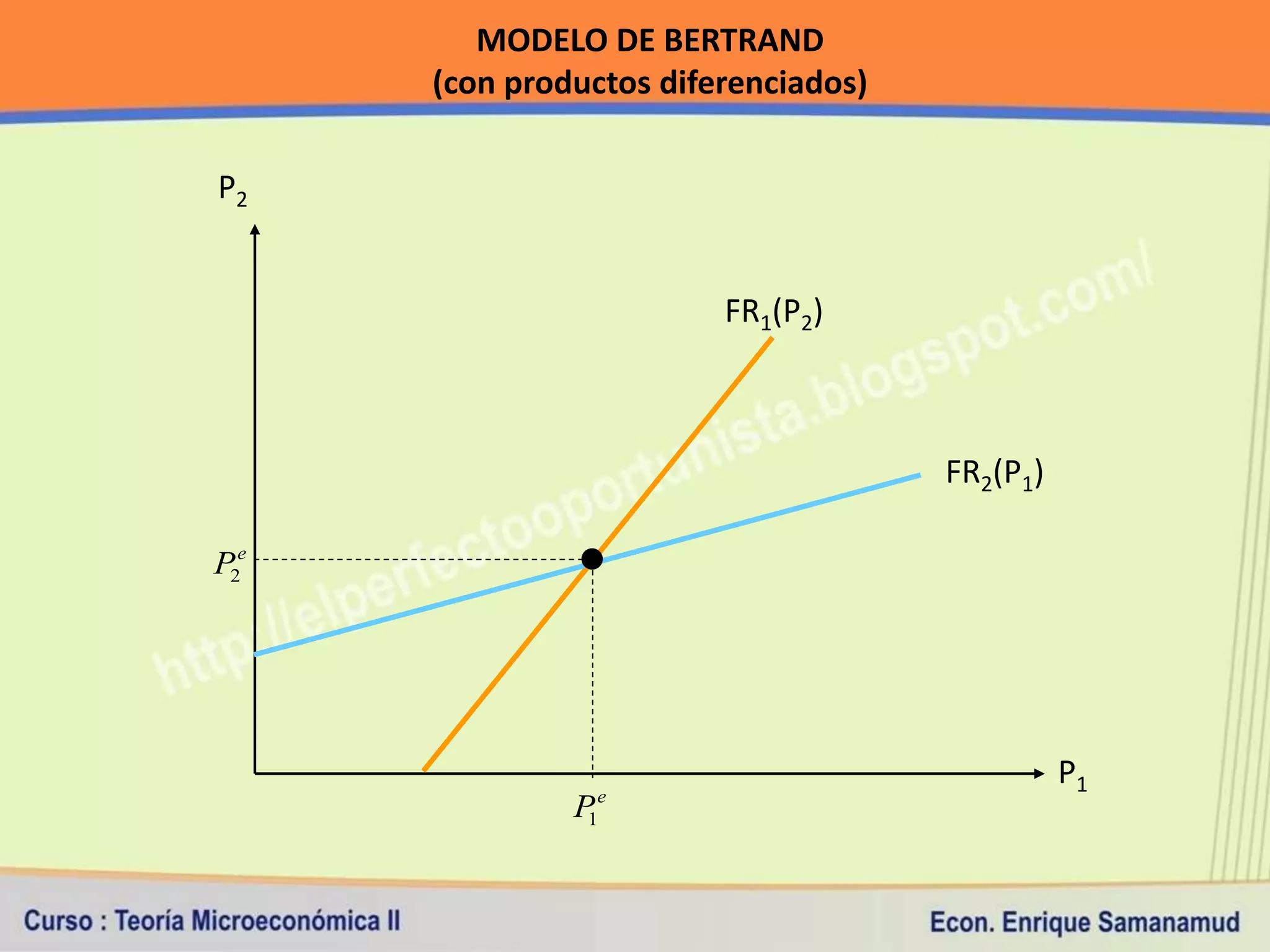
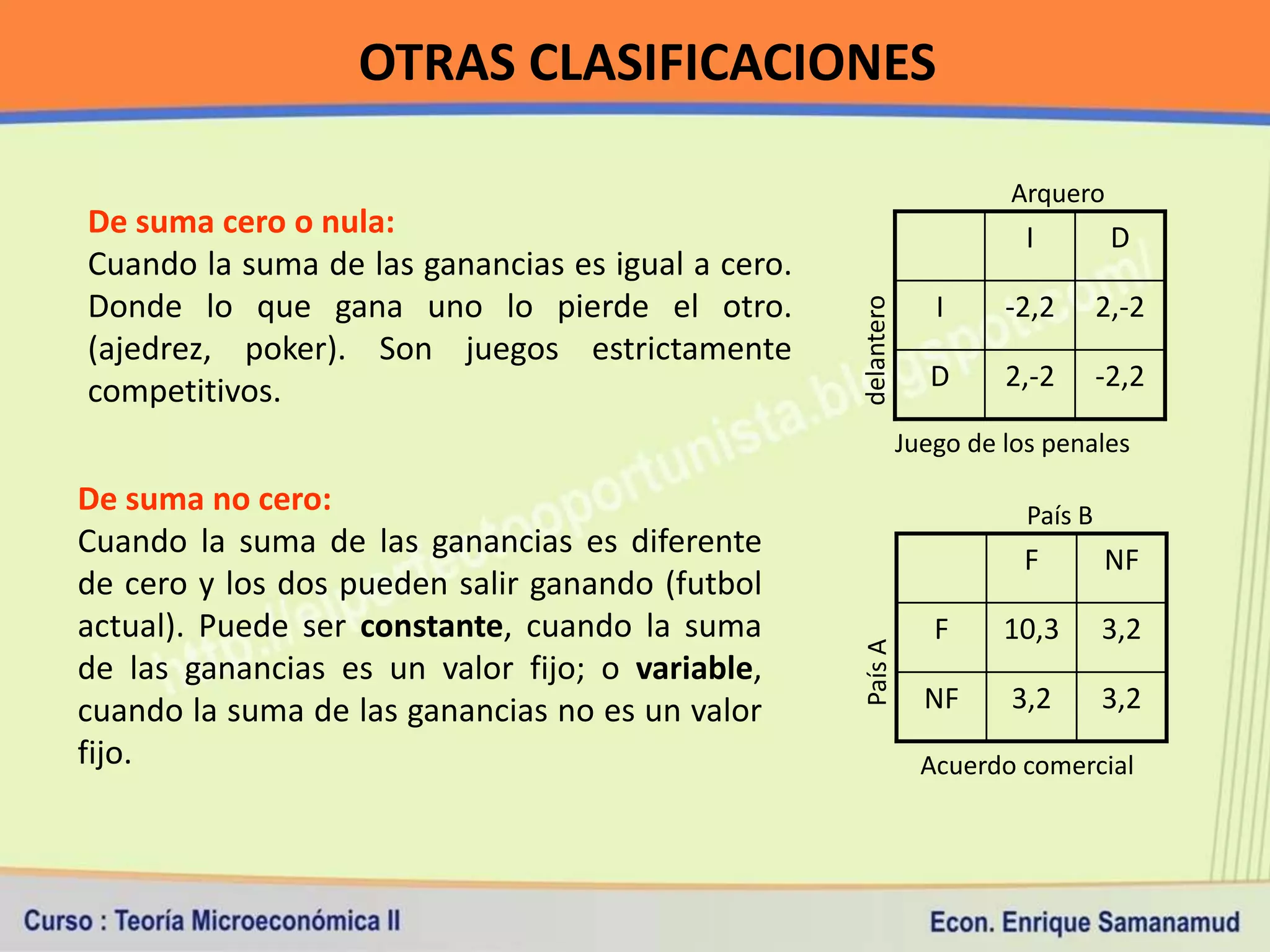
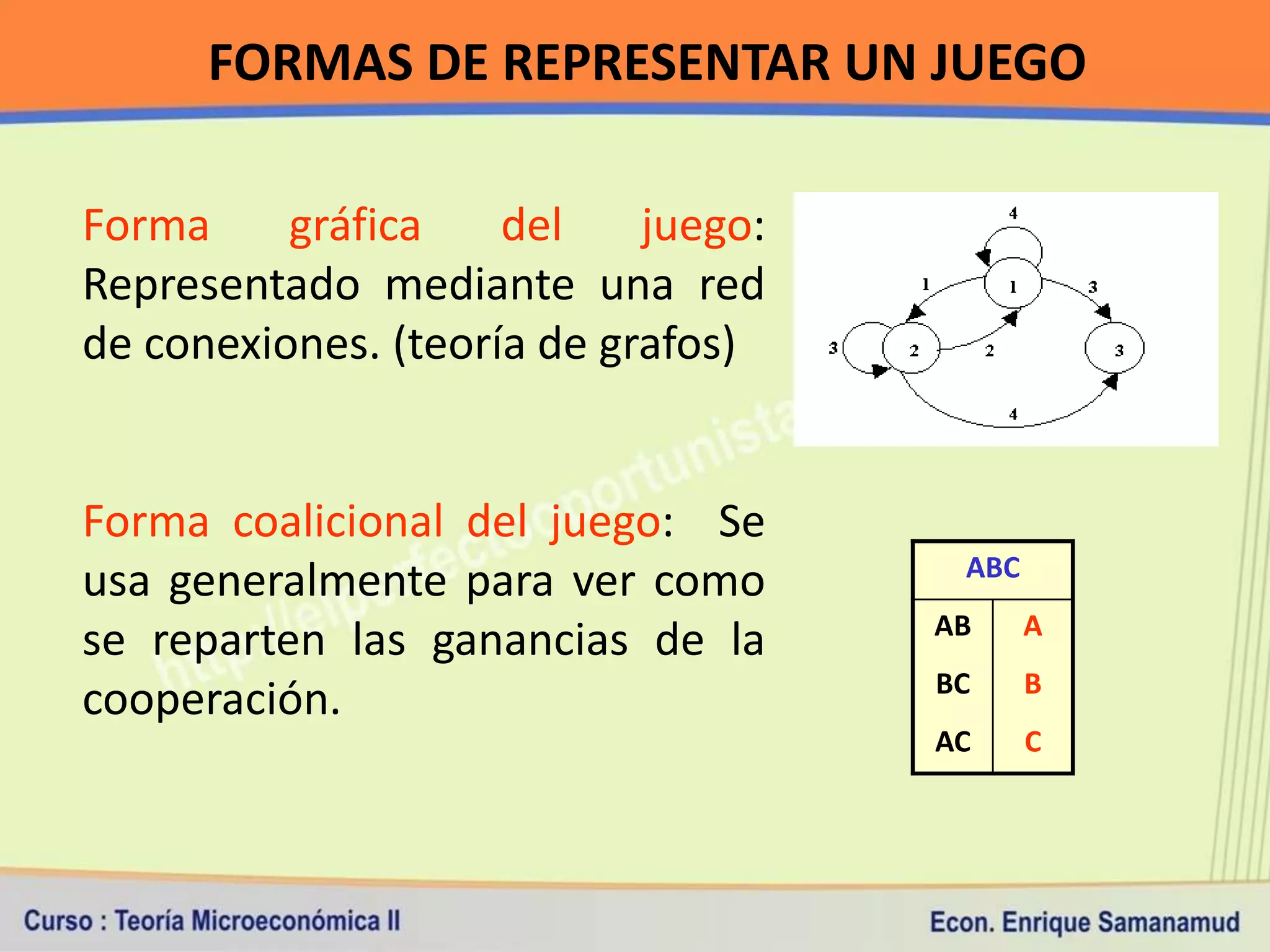
Este documento presenta conceptos clave sobre costos de producción y competencia perfecta. En la primera sección, explica la relación entre producción y costos, y los diferentes tipos de costos a corto y largo plazo. Luego, define los supuestos del modelo de competencia perfecta y cómo se determinan el ingreso y costo total, medio y marginal bajo este marco de competencia.





































































![VENTAS ATADAS (BUNDLING)
TIPO DE Procesador de Hoja de
CONSUMIDOR texto calculo
Tipo A 220 100
Tipo B 100 220
Si CMgPT = 50 y el CMgHC = 110
Si vendo cada artículo por separado:
Si PPT = 100 y PHC= 220
Beneficio = [2 (100) + 1(220)] – [2(50) + 1(110)] = 210 Estrategia
Ko.
Si PPT = 220 y PHC= 220
Estrategia
Beneficio = [1(220) + 1(220)] – [1(50) + 1(110)] = 280 OK. Mejor](https://image.slidesharecdn.com/tmiiv3-120701015356-phpapp01/75/Teoria-Microeconomica-II-89-2048.jpg)
![VENTAS ATADAS (BUNDLING)
TIPO DE Procesador de Hoja de
CONSUMIDOR texto calculo
Tipo A 220 100
Tipo B 100 220
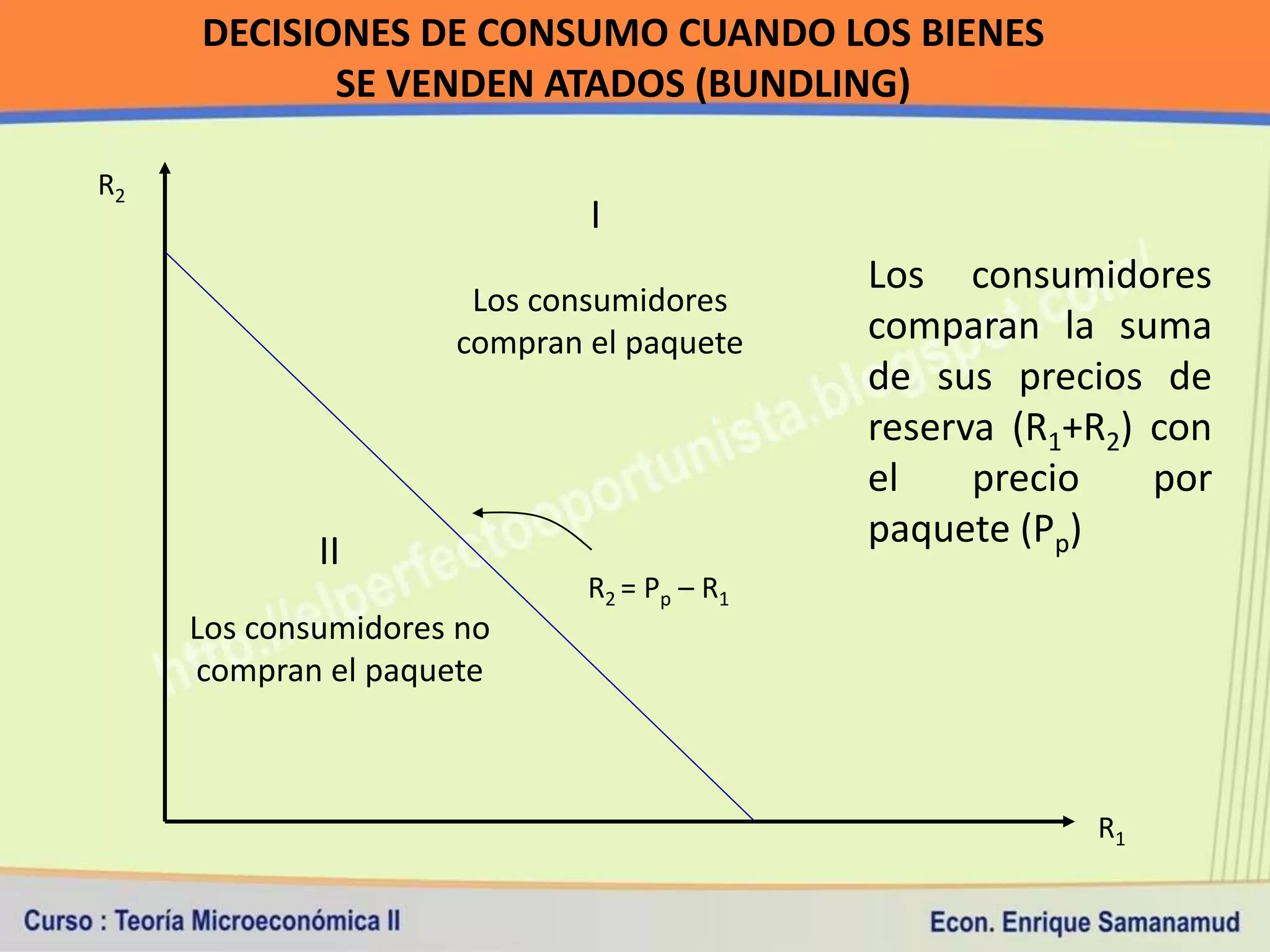
Si vendo los dos artículos juntos en un paquete: 160 < P(PT+HC) < 320 (R1 +
R2).
Fijo P(PT+HC) en 300.
Estrategia
Beneficios = 2(300) – [2(50) + 2(110)] = 280 Ko.
Fijo P(PT+HC) en 320. Estrategia
Beneficios = 2(320) – [2(50) + 2(110)] = 320 OK. mejor](https://image.slidesharecdn.com/tmiiv3-120701015356-phpapp01/75/Teoria-Microeconomica-II-90-2048.jpg)
![VENTAS ATADAS (BUNDLING)
TIPO DE Procesador de Hoja de
CONSUMIDOR texto calculo
Tipo A 220 100
Tipo B 100 220
Para la estrategia mixta necesito establecer un precio por separado que sea algo
igual al mayor valor de reserva. PPT = PHC= 225 y el precio del paquete debe ser algo
inferior a la suma de los precios de reserva P(PT+HC) = 319.
Beneficios = 2(319) – [2(50) + 2(110)] = 318 Estrategia OK.](https://image.slidesharecdn.com/tmiiv3-120701015356-phpapp01/75/Teoria-Microeconomica-II-91-2048.jpg)
![VENTAS ATADAS (BUNDLING)
TIPO DE Procesador de Hoja de
CONSUMIDOR texto calculo
Tipo A 220 100
Tipo B 100 220
Ahora si logro que el consumidor A compre por separado y el consumidor B opte
por el paquete haciendo PPT = 215 y PHC= 225 mejor:
Estrategia OK.
Beneficios = [1(319) + 1(215)] – [2(50) + 1(110)] = 324 Mucho mejor
Me conviene hacer venta atada al consumidor que tiene preferencia por el bien
cuyo CMg es el mas bajo.](https://image.slidesharecdn.com/tmiiv3-120701015356-phpapp01/75/Teoria-Microeconomica-II-92-2048.jpg)