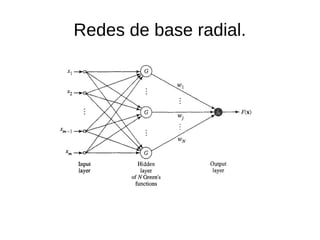
Rbn
- 1. Redes de base radial.
- 2. Teorema de Cover. ● “Un problema complejo de clasificación de patrones hecho en un espacio de alta dimensionalidad es mas probable ser separable que en un espacio de baja dimensionalidad”. ● Consideramos una familia de superficies que dividen el espacio de entrada en dos y sea: § que denota un conjunto de N patrones de entrada de dimensión m1 Cada patron es asignado en §1 ó §2
- 3. Teorema de Cover. Para cada patrón Χ∈§ definir un vector formado por valores reales: {ϕi(Χ)∣i=1,2,3...,m1} Una Dicotomia {§1, §2} de § es ϕ−separable siexiste un m1−dimensional vector W con el que podemos escribir : W (T) ϕ(Χ)>0 Χ∈§1 W (T) ϕ(Χ)<0 Χ∈§2
- 4. Teorema de Cover. ● Supongamos un conjunto de patrones de activación son elegidos de acuerdo a una probabilidad sobre el espacio de entrada. ● Sea entonces ● La probabilidad de que una dicótomia particular sea separable. Χ1, Χ2,. ..,Χn P(N ,m1)=(1 2 ) N−1 ∑ m=0 m1−1 (N−1 m )
- 5. Ejemplo ● Problema XOR. Salida 0 para vector de entrada (1,1) y (0,0) Salida 1 para vector de entrada (1,0) y (0,1) ● Definición de dos funciones Gaussinas ocultas:
- 6. Ejemplo.
- 7. Interpolación. ● La técnica funciones de base radial consiste en encontrar una función F de la siguiente forma: ● Donde ● Podemos concluir: F(Χ)=∑ i=1 N wi ϕ(Χ−Χi) F(Χ)=di i=1,2,.. N [ ϕ11 ... ϕ1N ϕ21 ... ϕ2N ... ... ... ϕN1 ... ϕNN ][ w1 w2 ... wN ]= [ d1 d2 ... dN ] ΦW =Χ
- 8. Problemas well-posed. ● El problema de reconstrucción f es llamado well-posed si cumple con: ● Existencia. ● Unicidad. ● Continuidad.
- 9. Teoria de la regularización. ● Los problemas ill-posed pueden ser resuletos. ● La teoría de regularización propone que en el momento de elegir la función F(x) se tengan en cuenta las siguientes cantidades: ● que es una medida de error cuadrático. ● Siendo este termino importante en la suavización de la curva.
- 10. Teoría de la regularización. ● La cantidad que se minimiza en la teoría de regularización es: ● Sea el diferencial del termino sub s, donde h es una función que donota una direccón podemos ver esto como una derivada funcional que es una generalizacion de la derivadas funcionales.
- 11. Teoría de la regularización. ● El diferencial del segundo termino es: ● De dos y tres tenemos que: ● Donde el parametro de regularizacion lambda toma valores de [0,inf)
- 12. Ecuacion de Euler-Lagrange. ● Como buscamos un punto extremo igualamos: ● Entonces podemos escribir:
- 13. Función de Green. ● Se llama función de green de un operador a una función tal que si F(x) entonces
- 14. Función de Green. ● Si L es un operador adjunto invariante a rotaciones y traslaciones entonces por lo que
- 15. Solución al problema de regularización. ● Sea L es un operador auto adjunto esto implica ● Entonces podemos concluir de la ecuacion de Euler- Lagrange
- 16. Solución al problema de regularización. ● Con esto notamos que la solucion al funcional de Tikhonov es una combinacion lineal de N funciones, la solucion cae en un espacion N- dimensional que tiene una base de funciones radiales.
