1. NÚMEROS COMPLEJOS

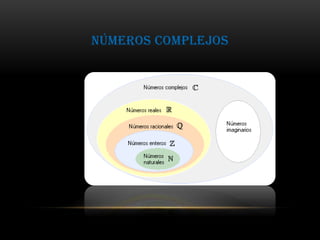
2. • Los números complejos conforman un grupo de cifras resultantes de
la suma entre un número real y uno de tipo imaginario. Un número
real, de acuerdo a la definición, es aquel que puede ser expresado
por un número entero (1,2,3,4,5…) o decimal (1.25, 1.78…). En
cambio, un número imaginario es aquél cuyo cuadrado es negativo.

3. HISTORIA DE LOS NÚMEROS COMPLEJOS
la historia de los números complejos se remota desde tiempos atrás. La
primera referencia de raíces cuadradas de números negativos se dio por
parte de los griegos matemáticos como Eron de Alejandría en el siglo I,
como resultado de una imposible sección de una pirámide. Seguidamente
Mahaviria de india decía que un negativo no tenia raíz cuadrada ya que
no era cuadrada. En tercer lugar viene Cardano de Italia en 1545 con esta
deducción las soluciones de las ecuaciones cubicas implican raíces
cuadradas de números negativos. Luego viene Descartes de Francia en
1637 introdujo los términos real e imaginario. Posteriormente en 1748
Euler de Suiza uso i para raíz de menos uno; y finalmente Gauss de
Alemania en 1832 introdujo el termino De Numero Complejo. Por otro lado,
personajes como Danés Wessel dio mayor auge aportando la
interpretación geométrica de los números complejos, y el matemático
Alemán Euler divulgo en gran medida la utilización de estos números.
Los números complejos surgieron por la necesidad de y para dar
soluciones a las raíces cuadradas negativas.

4. LA UNIDAD IMAGINARIA
Existen ecuaciones que no tienen solución en el conjunto de los
números reales, por ejemplo 𝑥2
┼9 = 0 no tiene solución en R
ya que no existe ningún número real que elevado al cuadrado
dé -9. Para solucionar problemas en los que aparezcan raíces
cuadradas de números negativos, es preciso ampliar el conjunto
de los números reales R, construyendo un nuevo conjunto, C,
de manera que R sea un subconjunto de C y de modo que en
ese nuevo conjunto se conserven las propiedades de las
operaciones y todos los números tengan raíz cuadrada. Para
ello se define la unidad imaginaria.
Unidad imaginaria i, es aquel número que elevado al cuadrado
da -1:
𝑖2
= -1; i= √−1
La ecuación 𝑥2
┼9= 0 tiene que cumplir 𝑥2
=-9
Entonces X= √-9= √9*√1=±3𝑖

5. OPERACIONES CON NUMEROS COMPLEJOS
La suma y diferencia:
Los números complejos se realiza sumando y restando las partes reales y las partes
imaginarias entre sí, respectivamente.
• (a + bi) + (c + di) = (a + c) + (b + d)i
• (a + bi) − (c + di) = (a − c) + (b − d)i
• EJEMPLO : (5 + 2i) + ( − 8 + 3i) − (4 − 2i ) = (5 − 8 − 4) + (2 + 3 + 2)i = −7 + 7i
La multiplicacion y la divicion:
El producto de los números complejos se realiza aplicando la propiedad distributiva del producto
respecto de la suma y teniendo en cuenta que i2 = −1.
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
EJEMPLO:
• (5 + 2 i) · (2 − 3 i) = 10 − 15i + 4i − 6i2 = 10 − 11i + 6 = 16 − 11i

6. REPRESENTACION GEOMETRICA DE UN NUMERO COMPLEJO
Sea z = a + b·i un número complejo en forma biónica. Su expresión
en forma cartesiana es z = (a, b). Consideremos el plano euclídeo
real R2, y en él un sistema de referencia ortonormal. A cada número
complejo z = a + b·i le hacemos corresponder un punto del plano
P(a, b); y recíprocamente, dado ese punto del plano le asociamos el
complejo z = a + b·i. Tenemos pues una biyección entre el plano
euclídeo real R2 y el cuerpo de los números complejos C.
El punto del plano P(a, b) correspondiente al complejo z = a + b·i
recibe el nombre de afijo de z. El ángulo que forma el vector OP con
el eje de abscisas recibe el nombre de argumento de z.
Además, el módulo del vector OP es: |OP| = (a2 + b2)1/2 = |z
que coincide con la distancia del punto P al origen de coordenadas.
Sea r = |z|. Si x es su argumento, se tiene que:
sen x = PA/OP = b/r ==> b = r·sen x
cos x = OA/OP = a/r ==> a = r·cos x
Luego podernos escribir z = a + b·i = r·cos x + i·r·sen x = r·(cos x +
i·sen x)

7. • FORMA POLAR:
Para representar un número complejo z n forma
polar se deben considerar el módulo y el
argumento de éste A |z| se le llama módulo y es la
raíz cuadrada de la suma de los cuadrados de la
componente real y la componente imaginaria. Se
suele escribir |z| o r y se puede pensar como la
distancia desde el origen hasta el número complejo
z si lo tenemos representado en el plano complejo.
Así pues, se tiene:
|z|= |a+b|= √𝑎2
+ 𝑏2
• a α se le llama el argumento del número
complejo z y es el ángulo que forma el número
complejo z en el eje real (en sentido positivo)
si lo tenemos representado en el plano
complejo. Así pues, se tiene:
β= arctan (
𝑏
𝑎
)
• FORMA TRIGONOMETRICA
Al representar un número complejo como un vector
en la forma ya descrita, éste viene definido de
manera única por dos valores:
MODULO: El módulo de un número complejo es
el módulo del vector determinado por el origen de
coordenadas y su afijo. Se designa por |z|.
z= a+bi
r= |2|= √𝑎2
+𝑏2
ARGUMENTO: Este es el Angulo del numero
complejo.
a= |2|*cos a
b= |2|*sen a
Dividiendo estas dos igualdades
𝑏
𝑎
=
2 ∗sen 𝜷
|2|∗cosβ
= tg 𝜷
FORMA TRIGONOMÉTRICA Y FORMA POLAR.
ESTA EXPRESIÓN, Z = R·(COS X + I·SEN X), RECIBE EL NOMBRE DE FORMA TRIGONOMÉTRICA DE Z, DONDE R ES
EL MÓDULO DE Z Y X SU ARGUMENTO.
DEFINIMOS LA FORMA POLAR DEL NÚMERO COMPLEJO Z = R·(COS X + I·SEN X) COMO RX.

8. GRAFICAS: FORMA POLAR- TRIGONOMETRICA
FORMA TRIGONOMETRICA

9. • Los números complejos se representan en
unos ejes cartesianos.
• El eje X se llama eje real.
• El eje Y se llama eje imaginario.
• El número complejo a + bi se representa:
• 1 Por el punto (a, b), que se llama su afijo.
REPRESENTACIÓN DE NÚMEROS COMPLEJOS EN EL PLANO
CARTESIANO
• Los afijos de los números reales se
sitúan sobre el eje real, X.
• Los afijos de los números imaginarios
se sitúan sobre el eje imaginario, Y.

10. ECUACIONES CON NUMEROS COMPLEJOS
• 𝑥2
+18=2 𝑦2
+40=4
𝑥2 = 2 − 18 𝑦2 =4-40
𝑥2
=-16 𝑦2
=-36
x= −16 y= −36
x= 4i y= 6i

11. La cultura se adquiere leyendo libros; pero el conocimiento
del mundo, que es mucho más necesario, sólo se alcanza
leyendo a los hombres y estudiando las diversas ediciones
que de ellos existen.” Lord Chesterfield.