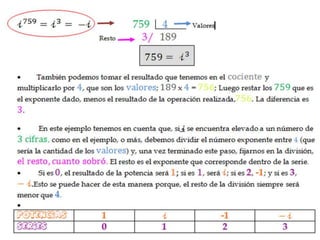
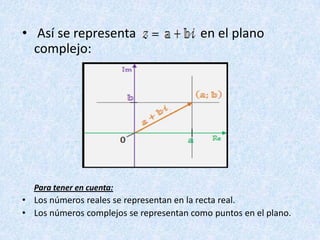
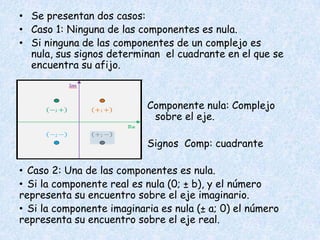
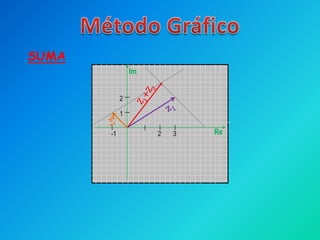
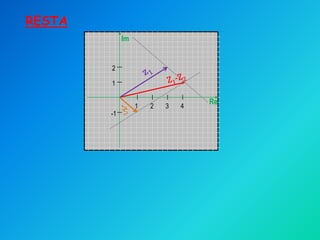
Este documento presenta información sobre números complejos. Contiene una lista de integrantes de un curso y luego explica la representación de números complejos en el plano complejo, con el eje real y el eje imaginario. También describe cómo sumar, restar y multiplicar números complejos usando sus partes reales e imaginarias, y provee ejemplos de estas operaciones.

1. INTEGRANTES:
Gómez, Carla.
Gordillo, Lucas.
Gorritti, Rocío.
Müller, Bruno.
Muñoz Sánchez, Juan.
CURSO: 2º 1ª Economía
COLEGIO JOSÉ M. ESTRADA
AÑO: 2011

5. NÚMEROS COMPLEJOS

6. .
Esquema de Posicionamiento de los
Números Complejos
• El conjunto de forma parte del conjunto de números , podría decirse que los
números son con parte IMAGINARIA cero, es decir:
• Y los números IMAGINARIOS son, también, números con parte nula, lo cual
significa:

7. Opuesto y Conjugado
Se denomina OPUESTO DE UN COMPLEJO al que se
obtiene de cambia el signo tanto a la parte Real como a
la Imaginaria.
El CONJUGADO DE UN COMPLEJO se obtiene
manteniendo el signo de la parte Real y cambiando el de
la parte Imaginaria
Complejo Opuesto Conjugado

8. ,
.
• El Plano Complejo
• Los Números REALES completan la recta numérica; por lo tanto,
para representar números no reales hay que salir de la recta real y
recurrir al plano, denominado PLANO COMPLEJO. En el Plano
Complejo, el EJE DE LAS ABSCISAS es el EJE REAL y el DE LAS
ORDENADAS, el EJE IMAGINARIO.
• El número complejo se representa mediante una FLECHA con
origen en (0 ; 0) y cuyo extremo es el punto de coordenada
• La componente real se representa en el eje real, y la
componente imaginaria , en el eje imaginario. La flecha es un
vector. Todas las propiedades de los vectores las cumplen también
los números complejos.

9. • Así se representa en el plano
complejo:
Para tener en cuenta:
• Los números reales se representan en la recta real.
• Los números complejos se representan como puntos en el plano.

10. • Se presentan dos casos:
• Caso 1: Ninguna de las componentes es nula.
• Si ninguna de las componentes de un complejo es
nula, sus signos determinan el cuadrante en el que se
encuentra su afijo.
Componente nula: Complejo
sobre el eje.
Signos Comp: cuadrante
• Caso 2: Una de las componentes es nula.
• Si la componente real es nula (0; ± b), y el número
representa su encuentro sobre el eje imaginario.
• Si la componente imaginaria es nula (± a; 0) el número
representa su encuentro sobre el eje real.

12. • Un poco de teoría para tener en cuenta…
• Suma de números complejos en forma binomica:
• La suma de dos complejos es otro número complejo; su parte real
es la suma de las partes reales de los sumandos y su parte
imaginaria es la suma de las partes imaginarias.
• (a + b i) + (c + d i) = (a + c) + (b + d i)
• La suma de complejos es conmutativa y asociativa
• La suma de números complejos tiene un elemento neutro que es el
complejo (0;0)
• La suma de un complejo y su opuesto es el elemento neutro z + (-z)
= (0;0)
• Resta de números complejos en forma binómica:
• La resta de dos números complejo es otro complejo que se obtiene
sumando al minuendo el opuesto del sustraendo.
• (a + b i ) – (c + d i ) = (a + b i ) + (-c – d i ) = (a – c ) + (b – d ) i
• La resta de números complejos, como la de los números reales, no
es conmutativa ni asociativa.

13. • Un ejemplo para suma y resta en números complejos

14. SUMA
Im
2
1
-1 2 3 Re

15. RESTA
Im
2
1
Re
1 2 3 4
-1

16. Teniendo 2 complejos:
• Z1= a + bi
• Z2= c + di
Entonces, la operación nos queda:
• Z1 x Z2 = (a + bi) x (c + di)
Aplicamos la propiedad DISTRIBUTIVA:
Z1 x Z2 = (a + bi) x (c + di)
Ahora, comenzamos a resolver:
En la diapositiva siguiente, te mostraremos un ejemplo.

18. El cociente de dos números complejos es otro número complejo que se obtiene
multiplicando el dividendo y el divisor por el conjugado del divisor (proceso similar a la
racionalización).
Esto es si y , entonces:
Luego:

19. EJEMPLO A)

20. EJEMPLO B)
Bibliografía: Matemática II – Editorial Santillana – Serie: PERSPECTIVA
Apuntes de Clases y Teoría de Carpeta